#1352

Вращающаяся дверь

Темы: [Элементарная геометрия]

В новом торговом центре проектируется вращающаяся дверь, которая на виде сверху представляет собой круг, разделенный на 4 равные части. Владельцы торгового центра знают, что самый большой товар, который у них будет продаваться, упаковывается в прямоугольные коробки шириной a, длиной b и высотой c. При этом транспортировать такую коробку можно только поставив ее на одну из граней. Определите, какой минимальный радиус должен быть у вращающейся двери, чтобы покупатель мог унести такой товар (высота двери может быть сколь угодно большой). Считается, что покупатель при попытке унести коробку действует самым очевидным для себя способом - размещает коробку так, чтобы угол один из углов коробки оказался в углу между створками двери. Размерами покупателя можно пренебречь

Входные данные

C клавиатуры вводятся натуральные числа a, b и c, не превосходящие 10000.

Выходные данные

Результат: выведите минимально необходимый радиус двери с точностью не менее 5 знаков после запятой.

Примеры

Входные данные

1 1 1

Выходные данные

1.4142136

#1353

В каком ухе жужжит?

Темы: [Элементарная геометрия]

Фрекен Бок находится в точке A (xa, ya) и, глядя прямо на Малыша, стоящего в точке B (xb, yb) задает вопрос: «В каком ухе у меня жужжит?». Естественно, у грозной домоправительницы жужжит в ухе, потому что в точке C (xc, yc) завис Карлсон со включенным мотором. Определите, какой ответ Малыша будет правильным.

Входные данные

С клавиатуры вводятся координаты точек A, B и С. Исходные данные являются целыми числами, по модулю не превышающими 1000.

Выходные данные

Выведите слово LEFT (заглавными буквами), если у домоправительницы жужжит в левом ухе, RIGHT – если в правом, BOTH – если жужжание и в левом и в правом одинаково.

Примеры

Входные данные

0 0 1 0 0 1

Выходные данные

LEFT

#1354

Собьем воздушный шарик

Темы: [Элементарная геометрия]

Винни Пух и Пятачок отправились воровать мед у пчел, и, в очередной раз влипли в неприятности. Пятачку опять потребовалось выстрелить из своего охотничьего ружья и пробить воздушный шарик, на котором Винни Пух поднялся к дуплу за медом. При этом желательно попасть именно в шарик, не задев медведя. Вычислите оптимальную позицию для стрельбы.

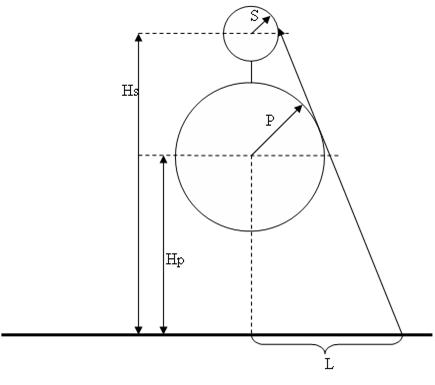
Поскольку Винни Пух очень любит покушать, то в данной задаче (да и не только в задаче) примем его за сферу радиуса P. Центр медведя находится на высоте Hp над уровнем земли. Строго над медведем , находится еще одна сфера, радиуса S – воздушный шарик; центр шарика находится на высоте Hs над уровнем земли. Центры обеих сфер находятся на одной вертикальной прямой. По понятным причинам гарантируется, что сферы не пересекаются J, однако могут касаться.

Считая, что ружье стреляет строго по прямой, вычислите минимальное расстояние L, на которое Пятачок должен отойти от места взлета, чтобы успешно поразить шарик. Шарик считается пораженным, если траектория пули хотя бы касается его поверхности; при этом если траектория пули касается медведя, то он считается невредимым.

Входные данные

C клавиатуры вводятся положительные целые числа P, Hp, S и Hs, не превосходящие 10000.

Выходные данные

Выведите минимальное расстояние от точки взлета, с которого можно поразить шарик из ружья с точностью не менее 5 знаков после запятой.

Примеры

Входные данные

1 9 10 21

Выходные данные

0.0000000

#1355

Векторы

Темы: [Способы задания графа] [Обход в ширину]

Источники: [ Личные олимпиады, Украинские олимпиады, 2004, 1 день, Задача A ]

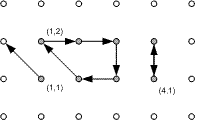На плоскости задано множество точек (x, y), где x, y – целые числа, 1≤x≤M, 1≤y≤N. Из каждой точки выходит ровно один из следующих векторов: (-1,-1), (-1,0), (-1,1), (0,1), (1,1), (1,0), (1,-1), (0,-1). Каждый вектор соединяет одну целочисленную точку плоскости с другой. Например, если из точке (2, 5) выходит вектор (1, 1), то он соединяет эту точку с (3, 6), но не наоборот.

Последовательность из двух и более точек плоскости a₁, a₂,…, a_k назовем циклом, если каждая точка a_i соединена вектором с a_i₊₁ (1≤i≤k-1), и a_k соединена вектором с a₁. Циклы считаются разными если они отличаются хотя бы одной вершиной.

Напишите программу, которая по информации о векторах, выходящих из точек плоскости, находит количество различных циклов.

Входные данные

Первая строка входного файла содержит два целых числа N (1≤N≤100) и M (1≤M≤100). Каждая из последующих N строк, содержит M пар чисел (т.е. 2≤M чисел). Пара x, которая находится в строке y, задает вектор в точке (x, y).

Выходные данные

Единственная строка выходного файла должна содержать целое число – количество циклов, образованных векторами.

Примеры

Входные данные

2 4 
-1 1 -1 1 -1 0 0 1
1 0 1 0 0 -1 0 -1

Выходные данные

#1358

Работники

Темы: [Перебор]

Источники: [ Личные олимпиады, Украинские олимпиады, 2004, 2 день, Задача A ]

На заводе каждая из N деталей может быть обработанной на одном из двух станков: A или B. Каждая деталь имеет порядковый номер от 1 до N. К обработке детали поступают последовательно, в соответствии со своими номерами. Количество деталей всегда четно.

Существуют правила, по которым определяется можно ли обрабатывать деталь на определенном станке.

Если на текущий момент на станке B было обработано такое же количество деталей, как и на станке A, то следующая деталь должна быть обработана на станке A.
В итоге на каждом из станков должно быть обработано одинаковое количество деталей.

Сколько людей, столько и мнений. Каждый из работников этого завода предложил свою последовательность обработки деталей, причем все предложения оказались разными, но удовлетворяющими правилам 1 и 2.

Напишите программу, которая по информации о количестве деталей N определяет максимально возможное количество работников завода.

Входные данные

Единственная строка входного файла содержит четное число N (2≤N≤28) – количество деталей которое необходимо обработать.

Выходные данные

Единственная строка выходного файла должна содержать целое число – максимально возможное количество работников завода.

Комментарий к примеру тестов

Первый работник считает, что на станке A необходимо обработать детали 1 и 2, а на станке B, соответственно, 3 и 4. Второй думает, что на станке A нужно обработать детали 1 и 3, а на станке B – детали 2 и 4. Других вариантов последовательности обработки не существует.

Примеры

Входные данные

Выходные данные