Алгоритмы(1657 задач)
Структуры данных(279 задач)
Интерактивные задачи(17 задач)
Другое(54 задач)
Робот движется по полю, которое состоит из N клеток, выстроенных в ряд. На каждой из клеток находится кубик определенного цвета.
До начала движения робот находится на первой клетке поля и не держит ни одного кубика. Находясь на клетке, робот может выполнить не более одного раза каждую из следующих операций: (1) положить кубик того же цвета, который лежит на текущей клетке; (2) поднять с клетки тот кубик, который находился там сначала. После этого робот перемещается на следующую клетку или останавливается, если текущая клетка последняя в поле.
Одновременно робот может держать не более K кубиков. На момент остановки робот не должен держать ни одного кубика.
Напишите программу, которая по информации о цвете кубиков и ограничении на количество кубиков, которое может держать робот, определяет максимальное общее количество кубиков, которое робот может перенести с места на место, двигаясь по полю.
Первая строка входного файла содержит символьную строку длинны N (1≤N≤1000). Строка состоит из маленьких букв латинского алфавита. Каждая буква соответствует клетке поля и определяет цвет кубика, который находится в этой клетке. Вторая строка содержит ограничение на количество кубиков, которое одновременно может держать робот K (1≤K≤25).
Единственная строка выходного файла должна содержать целое число — максимальное количество кубиков, месторасположение которых робот может изменить, двигаясь по полю.
Подзадачи и система оценки
Баллы за эту задачу будут начислены если ваше решение проходит все тесты
rgbbggrmcm 2
4
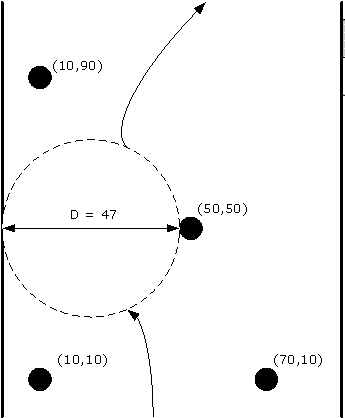 Единственный способ попасть в Зал Круглых Столов – пройти через Колонный Коридор. Стены Коридора изображаются на карте прямыми линиями, которые параллельны оси OY системы координат. Вход в Коридор находится снизу, а выход из Коридора в Зал – сверху. В Коридоре есть цилиндрические (на карте круглые) Колонны одинакового радиуса R.
Единственный способ попасть в Зал Круглых Столов – пройти через Колонный Коридор. Стены Коридора изображаются на карте прямыми линиями, которые параллельны оси OY системы координат. Вход в Коридор находится снизу, а выход из Коридора в Зал – сверху. В Коридоре есть цилиндрические (на карте круглые) Колонны одинакового радиуса R.
Напишите программу, которая по информации о размерах Коридора, и размещения Колонн определяет диаметр наибольшего из Круглых Столов, который можно пронести через такой Коридор, сохраняя поверхность Стола горизонтальной.
В первой строке входного файла заданы два числа XL и XR – x-координаты левой и правой стен Коридора. Во второй строке находится целое число R (1≤R≤1 000 000) – радиус всех Колонн. В третей – целое число N (1≤N≤200), которое задает количество Колонн. Далее следуют N строк, в каждой из которых по два числа – x- и y-координаты центра соответствующей Колонны.
Все входные координаты – целые числа, которые по модулю не превосходят 1 000 000.
Единственная строка выходного файла должна содержать одно число – искомый диаметр наибольшего Стола. Диаметр следует выводить с точностью 3 знака после десятичной точки (даже в случае, когда он окажется целым). Если нельзя пронести ни одного Стола, то ответ должен быть: 0.000
Точность 3 знака после точки, по обычным правилам округления, обозначает, что ответ, который выдается в выходной файл, должен отличаться от точного не более чем на 510-4 (т.е. на 0.0005). Например, если точный ответ 1.234567, то в файле должно находится число 1.235. Если точный ответ 5.0005, то необходимо округлять в большую сторону, т.е. в файл следует выдать 5.001
0 90 3 4 10 10 70 10 50 50 10 90
47.000
В новых элитных электричках каждому пассажиру положено сидячее место. Естественно, количество сидячих мест ограничено и на всех их может не хватить. Маршрут электрички проходит через N+1 станция, занумерованные от 0 до N. Когда человек хочет купить билет, он называет два числа x и y – номера станций, откуда и куда он хочет ехать. При наличии хотя бы одного сидячего места на этом участке на момент покупки ему продается билет, иначе выдается сообщение «билетов нет» и билет не продается. Ваша задача – написать программу, обслуживающую такого рода запросы в порядке их прихода.
В первой строке содержаться три числа N – количество станций (1 ≤ N ≤ 200 000), K – количество мест в электричке (1 ≤ K ≤ 1000) и M – количество запросов (1 ≤ M ≤ 100 000). В следующих M строках описаны запросы, каждый из которых состоит из двух чисел x и y (0 ≤ x < y <= N).
На каждый запрос ваша программа должна выдавать результат в виде числа 0 если билет не продается и 1 если билет был продан. Каждый результат должен быть на отдельной строке
5 2 4 0 4 1 2 1 4 2 4
1 1 0 1
Одно разбросанное на островах Океании государство решило создать сеть автомобильных дорог (вернее, мостов). По каждому мосту можно перемещаться в обе стороны. Был разработан план очередности строительства мостов и известно, что после постройки всех мостов можно будет проехать по ним с каждого острова на каждый (возможно, через некоторые промежуточные острова).
Однако, этот момент может наступить до того, как будут построены все мосты. Ваша задача состоит в нахождении такого минимального количества мостов, после постройки которого (в порядке строительства по плану) можно будет попасть с любого острова на любой другой.
Первая строка содержит два числа: N - число островов (1 ≤ N ≤ 100 000) и M – количество мостов в плане (1 ≤ M ≤ 200 000). В каждой следующей строке содержится описание моста – два числа x и y (0 ≤ x, y < N) – номера соединяемых островов.
Выведите в выходной файл одно число – минимальное количество построенных мостов, по которым можно попасть с любого острова на любой.
4 5 0 1 0 2 1 2 2 3 3 0
4
В одной военной части решили построить в одну шеренгу по росту. Т.к. часть была далеко не образцовая, то солдаты часто приходили не вовремя, а то их и вовсе приходилось выгонять из шеренги за плохо начищенные сапоги. Однако солдаты в процессе прихода и ухода должны были всегда быть выстроены по росту – сначала самые высокие, а в конце – самые низкие. За расстановку солдат отвечал прапорщик, который заметил интересную особенность – все солдаты в части разного роста. Ваша задача состоит в том, чтобы помочь прапорщику правильно расставлять солдат, а именно для каждого приходящего солдата указывать, перед каким солдатом в строе он должен становится.
Первая строка содержит число N – количество команд (1 ≤ N ≤ 50 000). В каждой следующей строке содержится описание команды: число 1 и X если солдат приходит в строй (X – рост солдата, натуральное число до 100 000 включительно) и число 2 и Y если солдата, стоящим в строе на месте Y надо удалить из строя. Солдаты в строе нумеруются с нуля.
На каждую команду 1 (добавление в строй) вы должны выводить число K – номер позиции, на которую должен встать этот солдат (все стоящие за ним двигаются назад). Выводите числа по одному в строке.
5 1 100 1 200 1 50 2 1 1 150
0 0 2 1