Алгоритмы(1657 задач)
Структуры данных(279 задач)
Интерактивные задачи(17 задач)
Другое(54 задач)
В Нумберляндии проблема: простое число \(p\) ревнует к другому простому числу \(q\). Оно думает, что в интервале от \(a\) до \(b\) включительно содержится больше чисел, которые делятся на большую степень \(q\) чем на степень \(p\). Помогите \(p\) справиться с сомнениями. Пусть \(a(n, x)\) – максимальное \(k\), такое, что \(n\) делится нацело на \(x^k\). Будем называть число \(n\) \(p\)-доминирующим над числом \(q\) если \(a(n, p) > a(n, q)\). Необходимо определить, сколько чисел из интервала от \(a\) до \(b\) включительно являются \(p\)-доминирующими над \(q\).
Первая строка содержит четыре целых числа \(a, b, p, q (1 ≤ a, b ≤ 10^{18}, 1 ≤ p, q ≤ 10^9)\). \(p ≠ q, p\) и \(q\) — простые.
Выведите одно число — сколько чисел из интервала от \(a\) до \(b\) включительно являются \(p\)-доминирующими над \(q\).
В примере числа 3, 9, 15 и 18 являются 3 доминирующими над 2.
1 20 3 2
4
Тестирование и контроль качества являются чрезвычайно трудоемкими этапами разработки ПО. Для облегчения этой задачи используются несколько различных техник. Одна из них называется верификацией. Model checking — верификация на базе модели Крипке.
Модель Крипке представляет собой набор \((P, S, R, L)\), где \(P\) – конечное множество высказываний, \(S\) — конечное множество состояний модели, \(R \in SxS\) – переход из одного состояния в другое. \(L \in SхP\) – отношение истинности (высказывание \(P\) в состоянии \(S\) истинно).
Отношение \(R\) будем считать рефлексивным, т.е. \(R(S, S)\) всегда существует.
Набор состояний π, начинающийся в состоянии s, представляет собой бесконечную последовательность состояний \(s_0, s_1,...,\) такую что \(s_0 = s\) и для любого \(i ≥ 0\) выполнено \((s_i s_{i+1})\) представляет собой переход.
В данной модели существует кванторы, применяемые к наборам и к состояниям, с помощью которых образуются формулы (элементарная формула, это высказывание, оно выполняется во всех своих истинных состояниях).
Проверить формулу \(f\) – означает найти все состояния, для которых она выполняется. Для произвольной формулы это сделать сложно. Ваша задача проще – проверить формулу E(xU(AGy)), где \(x\) и \(y\) - высказывания.
Первая строка содержит три натуральных числа \(n, m\) и \(k (1 ≤ n ≤ 10 000; 0 ≤ m ≤ 100 000; 1 ≤ k ≤ 26)\) – число состояний, переходов и высказываний. Каждая из следующих \(n\) строк описывает одно из состояний. Состояние \(i (1 ≤ i ≤ n)\) описывается числом \(c_i (0 ≤ c_i ≤ k)\) – количеством высказываний, которые истинны в этом состоянии, затем через пробел перечислены эти высказывания. Сами высказывания обозначаются первыми \(k\) маленькими латинскими буквами.
Следующие \(m\) строк описывают переходы. Каждое описание содержит два числа \(s\) и \(t\)
\((1 ≤ s, t ≤ n; s ≠ t)\) – переход из состояния \(s\) в состояние \(t\). Переходы из \(s\) в \(s\) существуют всегда и во входных данных не отражены. Никакие переходы не упомянуты дважды.
Последняя строка входных данных содержит формулу, которую надо проверить. Она всегда имеет вид E(xU(AGy)), где \(x\) и \(y\) – некоторые высказывания.
Первая строка выходных данных должна содержать число состояний, для которых формула верна. Следующие строки должны содержать номера этих состояний в возрастающем порядке.
7 8 2 1 a 1 a 2 a b 1 b 1 b 1 a 1 a 1 2 2 3 3 4 4 5 5 3 2 6 6 7 7 6 E(aU(AGb))
5 1 2 3 4 5
В королевстве \(N\); городов, пронумерованных от 1 до \(N\). Столица имеет номер 1. Каждый город окружен городской стеной с 4 воротами. Ворота пронумерованы следующим образом: ворота \(i\)-го города (1 \(\le\) \(i\) \(\le\) \(N\)) имеют номера 4\(i\)−3, 4\(i\)−2, 4\(i\)−1, 4\(i\). Через каждые ворота проходит ровно 1 дорога, которая ведет до некоторых ворот другого города (заметьте, что может существовать несколько дорог между двумя городами). По всем дорогам можно двигаться в обоих направлениях. Благодаря системе туннелей и мостов дороги не пересекаются вне городов.
Королевский гонец должен развесить копии Очень важного Королевского Указа на внешней стороне всех ворот каждого города. Гонец может свободно передвигаться от одних ворот к другим в пределах города, но вне города он может двигаться только по дорогам. Гонец выезжает из столицы и должен туда вернуться после выполнения задания.
Может ли гонец выполнить поручение, проходя через каждые ворота только один раз? Выход из города через ворота только для того, чтобы вывесить на их внешней стороне указ, а затем немедленное возвращение в город, считается за один проход через ворота.
Первая строка входного файла содержит целое число \(N\) (2 \(\le\) \(N\) \(\le\) 1000). Каждая из последующих 2\(N\) строк описывает одну дорогу и содержит 2 целых числа, разделенных пробелом: номера ворот, соединенных дорогой.
В первую строку выходного файла выведите Yes или No в зависимости от того, может ли поручение гонца быть выполнено, если проходить через ворота только один раз. В случае если это возможно, вторая строка выходного файла должна содержать 4\(N\) целых чисел, разделенных пробелом: номера ворот в порядке прохождения через них гонцом. Если существует несколько решений, выведите любое из них.
Рассмотрим числовую последовательность \(a_1\), ..., \(a_N\). Мы будем называть подстроку \(a_i\), …, \(a_j\), ..., \(a_k\) (1 \(\le\) \(i\) < \(j\) < \(k\) \(\le\) \(N\)) исходной последовательности холмом, если \(a_t\) < \(a\)t+1 для любого \(i\) \(\le\) \(t\) < \(j\) и \(a_t\) > \(a\) t+1 для любого \(j\) \(\le\) \(t\) < \(k\). В таком случае вершиной холма считается min{\(j\) − \(i\), \(k\) − \(j\)} . Аналогично, мы будем называть подстроку долиной, если \(a_t\) > \(a\)t+1 для любого \(i\) \(\le\) \(t\) < \(j\) и \(a_t\) < \(a\)t+1 для любого \(j\) \(\le\) \(t\) < \(k\). Тогда глубиной долины будет считаться min{\(j\)-\(i\), \(k\)-\(j\)}. Вычислите высоту самого высокого холма и глубину самой глубокой долины в данной последовательности.
В первой строке входного файла находится число \(T\) (1 \(\le\) \(T\) \(\le\) 100000) — количество тестовых блоков. Далее располагаются тестовые блоки, занимающие по 2 строки. Первая из двух строк содержит целое число \(N\) (1 \(\le\) \(N\) \(\le\) 1000000), во второй строке находятся члены последовательности, разделенные пробелом. Сумма значений \(N\) всех тестовых блоков в файле не превышает 100 000. Абсолютные значения членов последовательности не превышают 1 000 000.
Выходной файл должен состоять из \(T\) строк, в каждой строке по 2 числа: высота высочайшего холма и глубина самой глубокой долины. Если в тестовом блоке не существует долин или холмов, выведите число 0.
2 10 4 4 1 6 3 2 1 2 5 7 10 2 3 4 5 6 7 8 9 10 9
1 3 1 0
Представьте себе бесконечную клетчатую бумагу. Изначально все клетки белые, но некоторые из них можно закрасить черным.
Назовем две клетки 8-связными, если у них есть общая сторона или точка. 8-путем назовем последовательность клеток от A до B, так что все клетки в последовательности черные, и две соседние клетки в последовательности являются 8-связными. Набор черных клеток назовем рисунком, если существует 8-путь из каждой клетки набора в любую другую клетку этого набора.
Назовем две клетки 4-связными, если у них есть общая сторона. 4-путем назовем последовательность клеток от A до B, так что все клетки в последовательности белые, и две соседние клетки в последовательности являются 4-связными. Конечный набор белых клеток назовем пустотой, если существует 4-путь из каждой клетки набора в любую другую клетку этого набора и к нему невозможно добавить ни одной белой клетки так, чтобы предыдущее условие не нарушилось.
Будем говорить, что рисунок имеет высоту H и ширину W если он охватывается прямоугольником с высотой H и шириной W и не охватывается никаким прямоугольником меньшего размера. На иллюстрации показан рисунок с высотой 7 и шириной 9. По заданным числа H, W и N постройте рисунок высоты H, ширины W содержащий ровно N пустот.
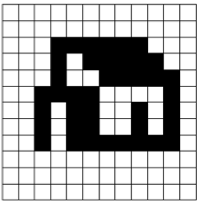
Входной файл содержит несколько тестовых блоков. Первая строка содержит число T (1 ≤ T ≤ 100) – количество тестовых блоков.
Каждая из следующих T строк описывает один тестовый блок. Описание состоит из целых чисел H, W и N (1 ≤ H, W ≤ 20, 1 ≤ N ≤ 200).
Выходной файл должен содержать следующую информацию для каждого тестового блока:
Если рисунок можно построить, то выведите любую допустимую фигуру, удовлетворяющую условию задачи, состоящую из H строк по W символов в каждой. Выводите символ “.” для обозначения черной клетки и символ “#” для обозначения белой клетки.
Если рисунок построить нельзя, выведите одну строку, содержащую слово “Impossible”.
Вывод данных для разных тестовых блоков разделяйте одной пустой строкой.
3 7 9 2 20 20 22 5 5 10
#......## #.#.....# #.##..... ....####. .#..##.#. .#..##.#. .#....... .#####.######.#####. ..###...####...###.. ...#.....##.....#... .................... ....##..##..#...#... ...#.#.#..#.##.##... ...###.#....#.#.#... ...#.#.#..#.#...#... ...#.#..##..#...#... .................... .................... .###..##..###...##.. ..#..#..#.#..#.#..#. ..#..#....###..#.... ..#..#..#.#....#..#. .###..##..#.....##.. .................... ...#.....##.....#... ..###...####...###.. .#####.######.#####. Impossible