Ромин папа работает в стремительно развивающейся корпорации «РосКошки». Сегодня папа решил показать своему сыну свою компанию, ведь он планирует, что со временем все его дети и внуки будут работать в «РосКошках». Рома — мальчик любознательный, поэтому он довольно быстро узнал всё о структуре корпорации.

Всего в «РосКошках» работает N сотрудников, у каждого из которых (кроме президента) есть один непосредственный начальник. Чтобы сотрудники не отвлекались по мелочам, президент запретил им во время работы общаться с кем-либо, кроме своих непосредственных подчинённых и начальника. Поэтому все сообщения сотрудникам приходится передавать через других сотрудников. Пока Рома без дела бродил по коридорам фирмы, он не только узнал для каждого сотрудника, сколько ему требуется минут, чтобы передать сообщение одному из своих подчинённых или начальнику, но и обнаружил, что в этой фирме работает сисадмин, который имеет особый статус: у него нет ни начальников, ни подчинённых, и он может передавать сообщения любому сотруднику фирмы, причём мгновенно. Но при этом, если у сотрудника есть хотя бы один подчинённый, он никогда не подойдёт к сисадмину с просьбой передать сообщение кому-либо. Рома осознал, что только что ему открылся новый способ передачи информации внутри корпорации, поэтому разузнал для каждого сотрудника, не имеющего подчинённых, сколько ему требуется времени, чтобы дойти до сисадмина.

Ромин папа хорошо осознаёт масштабы любопытства своего сына, поэтому, когда ему в очередной раз потребовалось передать своему другу срочное сообщение, он обратился к своему сыну. Помогите Роме минимизировать время, необходимое для передачи папиного сообщения его другу.

В недавно открытой раздевалке школы «Интеллектуал» решено поставить такие же шкафчики, как и в уже давно используемых раздевалках, но более новой модификации — состоящие из \(H*W\) ячеек. Напомним, что в каждую ячейку можно поставить ящичек, чтобы хранить в нём свои вещи. Однако новый директор школы запретил ученикам хранить свои вещи вне ящичков, поэтому тем, кому ящички не достались, приходится просить кого-то из владельцев соседних четырёх (или менее, если ячейка находится на границе) ячеек похранить свои вещи у себя. Если же ни у кого из соседей по ячейкам нет ящичков, этот ученик жалуется в администрацию.

Классному руководителю вдруг стало интересно, сколько же существует способов для каждого ученика определить, давать ли ему ящичек, чтобы никто не пожаловался в администрацию.

Количество учеников равно количеству ячеек.

В недавно открытой раздевалке школы «Интеллектуал» решено поставить такие же шкафчики, как и в уже давно используемых раздевалках, но более новой модификации — состоящие из \(H*W\) ячеек. Напомним, что в каждую ячейку можно поставить ящичек, чтобы хранить в нём свои вещи. Однако новый директор школы запретил ученикам хранить свои вещи вне ящичков, поэтому тем, кому ящички не достались, приходится просить кого-то из владельцев соседних четырёх (или менее, если ячейка находится на границе) ячеек похранить свои вещи у себя. Если же ни у кого из соседей по ячейкам нет ящичков, этот ученик жалуется в администрацию.

Классному руководителю вдруг стало интересно, сколько же существует способов для каждого ученика определить, давать ли ему ящичек, чтобы никто не пожаловался в администрацию.

Количество учеников равно количеству ячеек.

Иван-царевич в глубокой печали: морской царь поручил ему перепахать до утра огромную пустошь на морском дне и засеять рожью. Понятно, что без волшебства тут не справиться! По счастью, дочь морского царя, Василиса Премудрая, предложила Ивану-царевичу свою помощь.

У Василисы в сундуке хранятся грамоты с древними заклинаниями. Она втайне была в учении у самой Бабы-Яги, поэтому знает, что, чтобы творить волшебство, нужно произнести заклинание, да такое, в котором скрыто содержится нужное волшебное слово. Но достаточно ли сильны заклинания, хранящиеся в сундуке?

Вот что Василиса Премудрая узнала от Бабы-Яги:

Вхождение слова в заклинание — это подпоследовательность букв заклинания, совпадающая со словом. Буквы слова могут идти не подряд, но должны быть расположены в том же порядке. К примеру, заклинания «cadabra» и «barabara» содержат слово «abra», а заклинание «raba» — не содержит.

Вхождение называют скрытым, если никакие две его буквы не идут подряд. Например, в заклинание «abuba» слово «aua» входит скрыто, так как буквы вхождения (первая, третья и пятая) идут не подряд, а через одну. В заклинание «bauab» слово «aua», напротив, входит не скрыто.

Силой заклинания относительно волшебного слова считается количество скрытых вхождений в него этого волшебного слова. Например, волшебное слово «az» в заклинание «abazaba» входит два раза, но только один раз — скрыто, поэтому сила его равна единице.

Василиса хочет посчитать силу заклинания, которое она достала из сундука. Да вот беда — заклинание длинное, вхождений много, а ещё нужно отличать скрытые вхождения от не скрытых...

Зная заклинание и волшебное слово, посчитайте силу этого заклинания относительно данного волшебного слова.

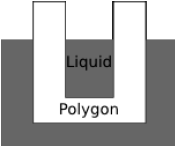
Многоугольник топят в жидкости, опуская его из воздуха с постоянной скоростью v метров в минуту. Жидкость разъедает многоугольник со всех сторон с постоянной скоростью c метров в минуту. Для точки (\(x\), \(y\)) внутри многоугольника, опускающейся вместе с ним, выясните, в какой момент разъедающая жидкость доберётся до этой точки.

Граница между воздухом и жидкостью проходит по прямой \(y\)=0. Жидкость разъедает многоугольник как двумерную фигуру. Многоугольник не поворачивается при опускании в жидкость, и в момент времени 0 он не касается жидкости.

В отличие от многоугольника, который считается двумерным, жидкость существует в трёх измерениях. Поэтому она проникает внутрь «дыр» в многоугольнике. Например, если многоугольник имеет форму «чашки», жидкость проникает «внутрь», как показано на рисунке.