Темы --> Информатика
    Язык программирования(952 задач)
    Алгоритмы(1657 задач)
    Структуры данных(279 задач)
    Интерактивные задачи(17 задач)
    Другое(54 задач)
---> 2656 задач <---
Источники
    Личные олимпиады(938 задач)
    Командные олимпиады(684 задач)
Страница: << 257 258 259 260 261 262 263 >> Отображать по:
#1989
Поклейка обоев
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Однажды майор Пронин затеял в квартире ремонт. В одной из стен на кухне по плану потребовалось последовательно проделать (N–1) прямоугольных вентиляционных отверстий с горизонтальными и вертикальными сторонами (0 < N < 101). Если оказывалось, что очередное отверстие пересекается с уже проделанными, то майор вырезал только нетронутую часть соответствующего прямоугольника.

Следующая стадия после ремонта – это поклейка обоев. В магазине напротив майор может заказать не более (2N–1)2 прямоугольных кусков обоев любых размеров c ненулевой площадью. Он хочет обклеить стену кусками обоев так, чтобы:

1. Вентиляционные отверстия не были заклеены даже частично.

2. Никакие два куска не пересекались (касаться сторонами они при этом могут).

На стене не осталось бы непокрытой области.

Рассмотрим декартову систему координат, оси которой параллельны сторонам отверстий и стены.

Входные данные

Сначала вводится число N (0 < N < 101), далее – описание N прямоугольников. Первый прямоугольник описывает положение стены в нашей системе координат, остальные (N–1) ― положения отверстий в порядке их появления. Стороны всех прямоугольников параллельны осям координат. Каждый прямоугольник задаётся координатами своих левого нижнего и правого верхнего углов: x1, y1, x2, y2. Координаты — целые числа, не превосходящие по модулю 31000, x1 < x2, y1 < y2.

Прямоугольники, обозначающие положение отверстий, могут пересекаться и касаться, поскольку это могло быть необходимо в ходе ремонта. Разумеется, все вентиляционные отверстия находятся в стене, то есть не выходят за границы первого прямоугольника.

Выходные данные

Вначале выведите количество кусков обоев K, которое нужно заказать в магазине (K должно быть не больше (2N–1)2). Далее выведите схему поклейки: K прямоугольников, обозначающих места расположения заказанных кусков. Для каждого прямоугольника нужно вывести координаты его левого нижнего и правого верхнего углов. Все координаты должны быть целыми числами. Гарантируется, что решение существует.

Если возможных способов несколько, выведите любой.

Примеры
Входные данные
2
-1 -1 2 2
0 0 1 1
Выходные данные
5
-1 -1 2 0
-1 0 0 2
0 1 1 2
1 0 2 1
1 1 2 2
#1990
Кодовый замок - 2
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Компания «Замки и замки» недавно разработала новый тип кодового замка, для размещения на воротах замков. Панель замка представляет собой прямоугольник шириной \(w\) ячеек и высотой \(h\) ячеек. В некоторых из них расположены кнопки.

Код на этом замке вводится одновременным нажатием \(k\) кнопок. Для того, чтобы код было легче запомнить, используемые в нем кнопки должны образовывать связную область. Область называется связной, если из любой клетки области можно добраться до любой другой, перемещаясь только между клетками этой области с общей стороной. Важным критерием надежности замка является число различных кодов, которые на нем можно набрать.

Для оценки надежности замков требуется написать программу для вычисления указанной величины.

Входные данные

В первой строке входного файла находятся три целых числа \(h\), \(w\) и \(k\) (\(1\le h,w\le 30\); \(1\le k \le 10\)). Каждая из последующих \(h\) строк содержит \(w\) символов. Символ «#» обозначает кнопку, а «.» — ее отсутствие.

Выходные данные

В выходной файл выведите единственное число — количество кодов, удовлетворяющих указанным требованиям.

Примеры

Входные данные Выходные данные
2 2 2
#.
## 		2
5 6 7
.#....
##.##.
..#.#.
.####.
.....# 		3

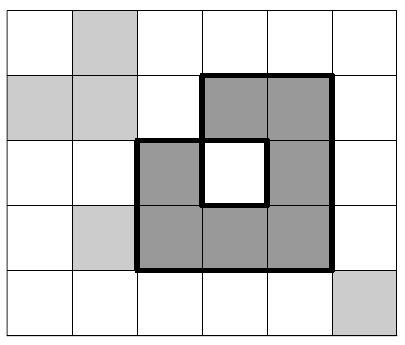
На рисунке изображен один из возможных кодов для второго примера.

#1991
Конденсация графа
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Вам задан ориентированный граф с \(N\) вершинами и \(M\) ребрами (\(1\le N\le 20 000\), \(1\le M\le 200 000\)). Найдите компоненты сильной связности заданного графа и топологически отсортируйте его конденсацию.

Входные данные

Граф задан во входном файле следующим образом: первая строка содержит числа \(N\) и \(M\). Каждая из следующих \(M\) строк содержит описание ребра — два целых числа из диапазона от \(1\) до \(N\) — номера начала и конца ребра.

Выходные данные

На первой строке выведите число \(K\) — количество компонент сильной связности в заданном графе. На следующей строке выведите \(N\) чисел — для каждой вершины выведите номер компоненты сильной связности, которой принадлежит эта вершина. Компоненты сильной связности должны быть занумерованы таким образом, чтобы для любого ребра номер компоненты сильной связности его начала не превышал номера компоненты сильной связности его конца.

Примеры
Входные данные
10 19
1 4
7 8
5 10
8 9
9 6
2 6
6 2
3 8
9 2
7 2
9 7
4 5
3 6
7 3
6 7
10 8
10 1
2 9
2 7
Выходные данные
2
1 2 2 1 1 2 2 2 2 1
#1993
Отожги мирных ферзей!
  
Темы: [Перебор]
ограничение по времени на тест
3.0 second;
ограничение по памяти на тест
64 megabytes

Расставить \(N\) ферзей на квадратной доске \(N\times N\) так, чтобы никакие два не били друг друга — очень непростая задача. Именно поэтому её поручили вам.

Входные данные

В единственной строке входного файла находится число \(4\le N\le 200\) — размеры доски.

Выходные данные

Выведите \(N\) чисел \(a\): \(a_i\) — это номер горизонтали, на которую вы поставите ферзя, занимающего \(i\)-тую вертикаль. Нумерация горизонталей идёт снизу вверх, от \(1\) до \(N\) (как на обычной шахматной доске).

Пример

Входные данные

Выходные данные

Комментарий

5

5 2 4 1 3

 

#....
..#..
....#
.#...
...#.

#1994
Форд-Беллман - 2
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
16 megabytes

В ориентированном взвешенном графе вершины пронумерованы числами от 1 до n. Если i<j, то существует ребро из вершины i в вершину j, вес которого определяется по формуле wt(i,j)=(179i+719j) mod 1000 - 500. Определите вес кратчайшего пути, ведущего из вершины 1 в вершину n.

Входные данные

Программа получает на вход одно число n (2≤n≤13000).

Выходные данные

Программа должна вывести единственное целое число - вес кратчайшего пути из вершины 1 в вершину n в описанном  графе.

Примеры
Входные данные
2
Выходные данные
117
Входные данные
3
Выходные данные
-164
Страница: << 257 258 259 260 261 262 263 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест