Темы --> Информатика
    Язык программирования(952 задач)
    Алгоритмы(1657 задач)
    Структуры данных(279 задач)
    Интерактивные задачи(17 задач)
    Другое(54 задач)
---> 2656 задач <---
Источники
    Личные олимпиады(938 задач)
    Командные олимпиады(684 задач)
Страница: << 281 282 283 284 285 286 287 >> Отображать по:
#2899
Вычеркивание двух
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Задана строка S, состоящая из маленьких букв латинского алфавита. Сколько различных строк можно получить при помощи вычеркивания ровно двух символов из S?

Входные данные

Входной файл содержит строку S, записанную в первой и единственной строке файла. Длина строки S от 2 до 100000 символов включительно. Строка S содержит только маленькие буквы латинского алфавита.

Выходные данные

Выходной файл должен содержать одно целое число, равное количеству различных строк, которые можно получить при помощи вычеркивания ровно двух символов из S

Примеры
Входные данные
abbccc
Выходные данные
5
#2903
Раскраска чисел
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Можно давать с гораздо меньшим TL

Профессор Васечкин хочет раскрасить целые числа от 1 до N таким образом, что если число A делится на число B, то числа A и B должны быть разного цвета. Помогите профессору найти такую раскраску, что число используемых цветов минимально.

Входные данные
Во входном файле записано число N (1 ≤ N ≤ 1000000).

Выходные данные
В первую строку выходного файла выведите M – число цветов в искомой раскраске. Во вторую строку выведите через пробел искомую раскраску чисел от 1 до N. Используемые числа должны быть обозначены числами от 1 до M.

#2904
Две строки
  
#2905
Скользящая симметрия
  

Движением плоскости называют такое преобразование плоскости, которое сохраняет попарные расстояния между точками, то есть если \(A_1\) и \(B_1\) – образы некоторых точек \(A\) и \(B\) при движении, то \(|A_1 B_1| = |AB|\).

Одной из разновидностей движения плоскости является скользящая симметрия. Скользящей симметрией называют композицию симметрии относительно некоторой прямой \(l\) и переноса на вектор, параллельный \(l\) (этот вектор может быть нулевым). На рисунке показан пример применения скользящей симметрии к отрезку.

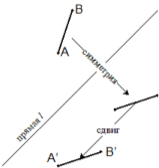
Известно, что любой отрезок можно перевести в любой другой отрезок такой же длины с помощью скользящей симметрии. Требуется по координатам двух различных точек \(A\) и \(B\) и двух точек \(A_1\) и \(B_1\), находящихся на таком же расстоянии друг от друга, как и точки \(A\) и \(B\), найти скользящую симметрию, переводящую точку \(A\) в точку \(A_1\), а точку \(B\) в точку \(B_1\).

Входные данные

В первой строке входного файла находятся четыре целых числа – координаты двух различных точек \(A\) и \(В\). Во второй строке также находятся четыре целых числа – координаты двух различных точек \(A_1\) и \(В_1\). Гарантируется, что \(|A_1B_1| = |AB|\). Все числа во входном файле по модулю не превышают \(1000\). Числа в строках разделены пробелом.

Выходные данные

Выведите в выходной файл описание искомой скользящей симметрии, которое представляется в следующем виде.

В первой строке должны выводиться координаты двух различных точек, лежащих на прямой \(l\), относительно которой выполняется симметрия, а во второй – координаты вектора, параллельного этой прямой, на который осуществляется перенос. Вещественные числа должны быть представлены не менее чем с 6 знаками после десятичной точки.

#2906
Форматирование текста
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Компания MacroHard разработала новый язык программирования PASCAL++. В этом языке имеется оператор вывода PrintLn, с помощью которого можно выводить строки любой длины. По стандарту языка, разработанному специалистами компании, некоторые комбинации символов в строке должны при выводе играть особую роль:

Комбинация Значение
\n Переход на новую строку
\t Вывод K пробелов (1 ≤ K ≤ 7), после чего курсор оказывается на позиции, имеющей номер вида 7N+1 (первая позиция каждой строки имеет номер 1).
\\ Вывод символа "\".
\XY, где X и Y – шестнадцатеричные цифры (0..9, A..F или a..f), причем \(XY \geq 20\) Вывод символа, имеющего ASCII код XY

К сожалению, главный программист забыл добавить в компилятор правильную процедуру форматирования. Поэтому строки выводятся прямо так, как они были записаны. Ваша задача состоит в том, чтобы преобразовать файл, полученный в результате выполнения одного или нескольких операторов PrintLn к форме, которая была задумана.

Входные данные

Входной файл содержит одну или несколько строк, каждая из которых является результатом работы неправильного оператора PrintLn. Размер файла не превышает 100000 байт.

(Все символы "\", встречающиеся во входном файле участвуют в создании какой-либо ключевой комбинации, т.е. сразу после любой последовательности, состоящей из нечетного количества подряд идущих символов "\", следует символ из набора {"n", "t", "\", "0".."9", "A".."F", "a".."f" }, причем в случае символа из множества {"0".."9", A".."F", "a".."f"}, затем следует еще один символ из этого множества.)

Выходные данные

Выведите в выходной файл, как выглядел бы данный текст, если бы он был преобразован по соответствующим правилам языка PASCAL++.

Примечание: никакой специальной обработки русских букв не требуется. Они могут отображаться неправильно при отладке или при выборе неправильной кодировки просмотра входного или выходного файла.

Страница: << 281 282 283 284 285 286 287 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест