Алгоритмы(1657 задач)
Структуры данных(279 задач)
Интерактивные задачи(17 задач)
Другое(54 задач)
Товарищ Иванов — очень богатый любитель гаджетов. Недавно он понял, что не может купить всех гаджетов, которые он хочет потому что их никто не производит. Поэтому он решил построить свою собственную Фабрику Гаджетов.
Фабрика Гаджетов будет построена на Сколковском шоссе. На этом шоссе сконцентрировано производство нанотехнологичной продукции, необходимой для производства гаджетов. Сколковское шоссе представляет собой прямую, а фабрики — точки на этой прямой (фабрики расположены вдоль дороги).
Для производства гаджета необходимо N нанотехнологичных деталей, M фабрик производит эти детали. Товарищ Иванов хочет минимизировать сумму квадратов расстояний до ближайших фабрик, производящих необходимые детали. Помогите ему и найдите все точки для которых эта сумма минимальна.
Первая строка входного файла содержит два натуральных числа N и M (1 ≤ n ≤ 10000; N≤ M ≤ 100000)
Следующие M строк содержат пары чисел xi и pi, xi – координата i-ой фабрики, а pi – идентификатор детали, которую производит данная фабрика (xi ≤ 100000; xi ≤ xi +1; 1 ≤ pi ≤ N).
Для каждой детали существует хотя бы одна фабрика, которая производит эту деталь.
Первая строка выходного файла должна содержать целое число K — количество точек, где может быть расположена Фабрика Гаджетов.
Следующие K строк должны содержать координаты этих точек в возрастающем порядке. Значения должны выводится с точность 10-6.
3 5 -1 3 0 1 2 3 4 2 5 2
1 2.0
2 5 1 1 2 2 3 1 4 2 5 1
4 1.5 2.5 3.5 4.5
Пусть G=(V, E) – произвольный ориентированный граф. Для каждой вершины x этого графа введем множество Next(x) как множество всех вершин, в которые ведут дуги, выходящие из вершины x.
Пусть F – функция, принимающая целые неотрицательные значения, определенная на вершинах графа G. Функция F называется функцией Гранди, если для каждой вершины x графа G выполняется условие F(x)=min{n≥0|n≠F(y) ни для какой вершины y из Next(x)}.
Рассмотрим класс ориентированных графов, у которых в каждую вершину входит ровно одна дуга. Напишите программу, которая получает на вход некоторый граф из описанного выше класса и находит функцию Гранди для этого графа, если она существует.
Входной файл содержит описание ориентированного графа. В первой строке файла находится целое число N (2 ≤ N ≤ 100000), равное количеству вершин графа. В i-й из следующих N строк находится одно целое число Pi (1 ≤ Pi ≤ N; Pi ≠ i), равное номеру вершины, из которой выходит та дуга, которая ведет в вершину с номером i.
Eсли для графа, описанного во входном файле, не существует функции Гранди, то выходной файл должен содержать одну строку со словом "NO". В противном случае, файл должен состоять из N строк, в i-й из которых должно быть записано одно целое число Fi – значение найденной функции Гранди для вершины с номером i. Если существует несколько функций Гранди для графа, описанного во входном файле, то выведите любую из них.
4 2 4 4 1
YES
3 3 1 2
NO
4 4 3 2 1
YES
Совсем недавно Али-Баба узнал от своего брата Касима об удивительной игре Го. В Го играют на прямоугольной доске – гобане, расчерченном вертикальными и горизонтальными линиями. Все линии пронумерованы. В игре участвуют два игрока, которые по очереди выставляют на гобан камни – специальные круглые фишки. Каждый камень ставится на незанятую точку пересечения линий доски (пересечения называют пунктами). У одного игрока – черные камни, у другого – белые. Камни одного цвета, смежные по вертикали, либо по горизонтали (но не диагонали), объединяются в группу. Одиночный камень также считается группой.
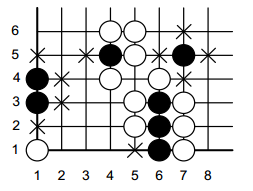
Один из способов набрать очки в Го – захватить камни противника. Каждый камень может иметь от двух до четырех смежных с ним пунктов (по вертикали и горизонтали, но не по диагонали). Если такой пункт не занят камнем, то он называется «дамэ». Дамэ группы – это все дамэ камней, составляющих группу. Как только оппонент своими камнями закрывает все дамэ чужой группы, то эта группа считается захваченной и снимается с доски. Если у группы осталось лишь одно дамэ, то говорят, что эта группа находится в «атари» т.е. на один шаг от захвата соперником.
Дамэ черных камней на рисунке отмечены крестиком. Группа черных из камней (1, 3) и (1, 4) имеет 4 дамэ. Группа (6, 1), (6, 2) и (6, 3) имеет одно дамэ и находится в атари. Черный камень (4, 5) также находится в атари. Помогите Али-Бабе, который всегда играет черными, определить, какие его группы находятся в атари.
Описание каждого теста начинается со строки, содержащей число N – размерность игровой доски (6 ≤ N ≤ 19). Далее следует N строк по N символов каждая. Каждый символ описывает один пункт доски. «B» означает черный камень, «W» – белый, «.» означает пустой пункт. Все группы на доске имеют хотя бы одно дамэ.
Выводите одно число – количество групп черных камней, находящихся в атари.
9 ......... ......... ......... ...WW.... ...BW.B.. B..W.W... B...WBW.. ....WBW.. W....BW..
2
6 WB.WBB .B.W.B ..WW.W WWW..W ..W... BBW...
1
Всем известно, что в позапрошлом веке ковбои занимались перегоном скота. Перегон скота всегда считался опасным делом. Ковбой Джон, готовясь к очередному перегону, изучал план местности. Так как местность гористая, то добраться из одного поселения в другое можно только по дорогам, возможно через другие поселения. Главной опасностью на пути были бандиты, проживающие в разных населенных пунктах, и организующие группировки для нападения на ковбоев. Чтобы их разобщить, Джон разработал гениальный план полной изоляции поселений друг от друга.
Посоветовавшись с напарниками, Джон пришел к выводу, что временно дороги можно вывести из строя, устроив камнепад. Под покровом ночи можно выехать из одного населения в другое, остановиться где-то посреди дороги и устроить камнепад так, чтобы по этой дороге нельзя больше проехать никому. Камни падают позади повозки, поэтому обратной дороги нет. Но зато можно ехать в другой населенный пункт, и если из него существуют дороги, то и их можно вывести из строя.
Сам Джон этого сделать не может, только он знает тайные тропы и должен перегонять стадо. Поэтому он решил использовать наемников. Наемники есть в любом поселении и в любом количестве, однако, за каждого из них приходится платить немалую сумму, поэтому Джон хочет потратить как можно меньше денег. Помогите Джону определить минимальное число наемников, которые смогут привести в непригодность абсолютно все дороги и изолировать все поселения.
В первой строке каждого теста находятся два целых неотрицательных числа N (0 < N < 1000) – количество поселений и M (0 ≤ M ≤ 100 000) – количество дорог, их соединяющих. Далее следует M строк, содержащих описание дорог. В i-й строке находятся два натуральных числа V и U (1 ≤ V, U ≤ N) – номера поселений, которые соединяет i-я дорога. Между двумя различными поселениями существует не более одной дороги, но может существовать несколько маршрутов. Нет дорог, которые образуют петлю, исходящую из поселения и ведущую в него же, не заходя в другие поселения. Не гарантируется, что существует маршрут между любой парой поселений. Маршрутом называется такая последовательность поселений s1-s2- … -sn, что любые два последовательных поселения si и si+1 соединены дорогой..
Выведите минимальное количество наемников, необходимое для изоляции всех поселений.
6 6 1 2 2 3 1 3 4 5 5 6 4 6
2
Андрей популярный писатель-фантаст, он проводит мастер-классы для своих читателей. Наиболее популярным из них является Alien Communication Masterclass (ACM), на котором он учит как поступать в случае встречи с пришельцем или нахождении инопланетного артефакта.
Одна из лекций посвящена извлечению информации из инопланетных записей. Исследования Андрея базируется на математических формулах пришельцев, которые могут дать некоторые знания об организмах пришельцев (например, мы используем десятичную систему счисления потому что у нас 10 пальцев на верхних конечностях).
Предположим для простоты, что пришельцы используют те же самые цифры, что и мы и таким же образом трактуют сложение, вычитание, умножение, скобки и равенство.
Для своей лекции Андрей хочет найти пример равенства, которое выполняется в системах счисления с основаниями a1, a2, .., aN, но не выполняется в системах счисления с основаниями b1, b2, …, bM. Найдите для него пример такой формулы.
Первая строка входного файла содержит два целых числа N и M (1 ≤ N, M ≤ 8).
Вторая строка содержит N чисел a1, a2, .., aN
Третья строка содержит M чисел b1, b2, …, bM
Все числа ai и bi различны и лежат в пределах от 2 до 10.
Вывод должен представлять собой корректное математическое равенство, которое выполняется в системах счисления с основаниями a1, a2, .., aN и не выполняется в системах с основаниями b1, b2, …, bM.
Равенство может содержать цифры от 0 до 9, знак плюс +, минус и унарный минус –, знак умножения *, скобки ( и ) и знак равенства =. Знак равенства должен быть ровно один.
Все пробельные символы будут проигнорированы при проверке. Количество непробельных символов не должно превышать 10000.
1 2
2
3 9
(10 - 1) * (10 - 1) + 1 = 10
2 2
9 10
2 3
2 + 2 = 4