Темы --> Информатика
    Язык программирования(952 задач)
    Алгоритмы(1657 задач)
    Структуры данных(279 задач)
    Интерактивные задачи(17 задач)
    Другое(54 задач)
---> 2656 задач <---
Источники
    Личные олимпиады(938 задач)
    Командные олимпиады(684 задач)
Страница: << 332 333 334 335 336 337 338 >> Отображать по:
#3365
Дорожное движение
  
ограничение по времени на тест
3.0 second;
ограничение по памяти на тест
64 megabytes

В городе Z в час пик очень оживленное движение. Неправильно выбранный маршрут может на долгое время задержать вас в пути. Вам известно, что схема города представляет собой N горизонтальных и M вертикальных односторонних дорог, образующих прямоугольник N-1 на M-1 километр. На пересечении каждой вертикальной и горизонтальной дороги находится перекресток, на котором можно изменить направление движения. Заметьте, что для изменения направления движения нужно сначала полностью затормозить.
Вы находитесь в точке (1, 1), или другими словами, в левом нижнем углу города. Движение происходит слева направо и снизу вверх. Вам необходимо добраться до точки (N, M) за наименьшее время. Проблема в том, что на каждой дороге свой скоростной режим и максимальное ускорение, которое можно развить, разное для каждой дороги (и равно, соответственно, \(A_i\) км/\(c^2\) для вертикальной дороги с номером i и \(B_j\) км/c2 для горизонтальной дороги с номером j). При этом скорость на дорогах не ограничена. Ускорение и торможение происходит по стандартным физическим законам.
Однако ваше преимущество состоит в том, что вы хорошо знаете город и можете попасть напрямую с перекрестка (i, j) на перекресток (i+1, j+1), в объезд главных дорог (перед этим также нужно полностью затормозить). Время, необходимое для этого, не зависит от номера перекрестка и равно C. Дороги пронумерованы в порядке, соответствующем направлению движения. Напомним, что движение на всех дорогах одностороннее.

Входные данные

В первой строке входного файла расположены числа \(N\), \(M\) и \(C\) (\(1 \leq N, M \leq 1000\), \(10^{-3} \leq C \leq 10\)). Далее, во второй и третьей строках расположены числа \(A_1\), ..., \(A_N\) и \(B_1\), ..., \(B_M\), соответственно (\(10^{-3} \leq A_i, B_i \leq 10\)).

Выходные данные

В первой строке выходного файла выведите искомое время с восемью знаками после запятой. Во второй строке укажите количество перекрестков \(K\), через которые проходит маршрут, включая первый и последний. Далее, в \(K\) строчках выведите координаты соответствующих перекрестков. Выведите координаты только тех перекрестков, где нужно затормозить(учтите, что после каждого переезда по диагонали нужно затормозить).

Примеры
Входные данные
2 2 4.0
2.0 2.0
2.0 2.0
Выходные данные
2.82842712
3
1 1
1 2
2 2
#3366
Дятлы
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
Необходимо проверить отсутствие циклов

В парке растут два очень высоких дерева, на стволе каждого из которых расположены дупла одно под другим на равном расстоянии друг от друга. Однажды N дятлов решили заселить эти дупла. Некоторые из них знакомы и поэтому хотели бы иметь возможность летать друг к другу в гости. Дятлы летают прямолинейно и очень быстро. Чтобы уменьшить вероятность столкновения, они решили селиться по следующему принципу:

Каждые две дятла, которые хотят летать друг к другу в гости, должны жить на разных деревьях Отрезки, соединяющие дупла знакомых между собой дятлов не пересекаются (однако их концы могут совпадать).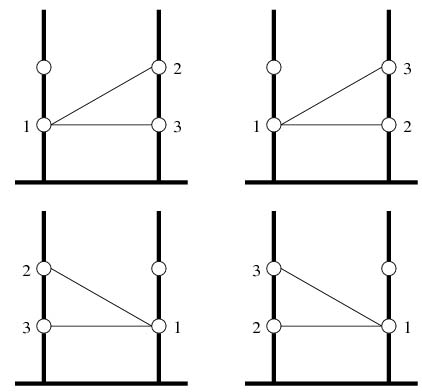

Кроме того, дятлы хотят жить как можно ниже, т.е. на каждом из деревьев они занимают дупла подряд, начина снизу. На каждом из деревьев больше дупел, чем общее количество дятлов.
Как известно, у дятлов очень маленький мозг. Поэтому вам следует подумать за них и сообщить, сколькими способами они могут разместиться в дуплах. Т.к. дятлы также плохо воспринимают большие числа, ответ следует вывести по модулю K.

Входные данные

В первой строке содержатся три числа: \(N\) – количество дятлов (\(1 \leq N \leq 10^6\)), \(M\) – количество пар знакомых дятлов (\(1 \leq M \leq 10^7\)) и число \(K\) (\(1 \leq K \leq 2\times 10^6\)). Дятлы занумерованы от \(1\) до \(N\). В следующих \(M\) строках заданы два числа \(a_i\) и \(b_i\) (\(1 \leq a_i, b_i \leq N\)), задающие пару знакомых дятлов.

Выходные данные

Вывод должен содержать одно число: количество вариантов размещения по модулю K.

Примеры тестов

Примеры
Входные данные
3 2 10
1 2
1 3
Выходные данные
4
Входные данные
4 4 17
1 2
1 3
4 2
3 4
Выходные данные
0
#3367
Две строки
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Вам заданы две строки длиной не более 50000 символов. Назовем строку хорошей, если она удовлетворяет условию, что если дописать ее в конец самой себе достаточно много раз, то в полученной строке будут содержаться в качестве подстрок обе заданные строки. Например, для строк “ababa” и “bab” строка “ab” является хорошей – действительно, дописав ее в конец себе два раза, мы получим строку “ababab”, которая содержит обе заданные строки в качестве подстрок. Для двух заданных строк найдите самую короткую хорошую строку.

Входные данные

Входной файл содержит две заданные строки. Строки состоят из символов с ASCII-кодами от 33 до 127. Длина каждой из них не превышает 50000.

Выходные данные

Выведите в выходной файл ответ на задачу. Если существует несколько различных оптимальных хороших строк, то выведите любую.

Примеры
Входные данные
ababa
bab
Выходные данные
ab
#3368
Следующий!
  

Отсортируем все числа 0 до N включительно по количеству единиц в двоичном представлении. Таким образом, \(4=100_2\) идет раньше чем \(3=11_2\), так как в двоичном представлении имеет на одну единицу меньше. В случае одинакового количества единиц раньше идет то число, которое меньше.

Пример сортировки для N=7: 0,1,2,4,3,5,6,7.

Даны числа N и K. Требуется найти следующее после K в указанном выше порядке.

Входные данные

В первой строке входного файла содержится число \(N\) (\(1 \leq N \leq 10^{100}\)). Вторая строка содержит число \(K\) (\(0 \leq K \leq N\)).

Выходные данные

В выходной файл выведите следующее за K число. В случае, если K - последнее число, то выведите -1.

Примеры
Входные данные
10
4
Выходные данные
8
Входные данные
12
11
Выходные данные
-1
#3369
Поиск подстроки
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
Z-функция

У Андрюши есть маленькая сестричка Аня. Она любит писать сообщения своему другу Гоше. Она хочет, чтобы никто не мог прочитать ее сообщения, поэтому она шифрует их подстановочным шифром. Подстановочный шифр заменяет каждый символ в сообщении на какой-либо еще, при этом равные символы заменяются на равные, а различные — на различные. Например, при шифровании с помощью подстановочного шифра e – a, l – b, o – w, v - c слово "love" оказывается зашифровано как "bwca".

Андрюша недавно перехватил одно из Аниных сообщений t и хочет выяснить, встречается ли там текст р. А именно, он хочет найти все позиции i, такие что существует подстановочный шифр, такой что t[i..i+|р| — 1] представляет собой зашифрованную версию р. Будем называть такие позиции потенциальными вхождениями р в t.

Помогите Андрюше найти все потенциальные вхождения р в i.

Входные данные

Первая строка входного файла содержит t. Вторая строка входного файла содержит р. Каждая строка состоит из символов с ASCII кодами от 33 до 126. Длина р не превышает длины t. Длина t не превышает 200 000. Обе строки непусты.

Выходные данные

Первая строка выходного файла должна содержать к — количество потенциальных вхождений р в t. Вторая строка должна содержать к целых чисел — позиции потенциальных вхождений. Позиции в строке нумеруются, начиная с 1. Позиции следует перечислить в возрастающем порядке.

Примечание

За тесты в которых \(t \le 1000\) начисляется 50% баллов. За остальные тесты тоже 50%. Баллы начисляются только при прохождении всех тестов группы.

Примеры
Входные данные
abacabadabacaba
aba
Выходные данные
7
1 3 5 7 9 11 13
Входные данные
abacabadabacaba
love
Выходные данные
0
Страница: << 332 333 334 335 336 337 338 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест