Алгоритмы(1657 задач)
Структуры данных(279 задач)
Интерактивные задачи(17 задач)
Другое(54 задач)
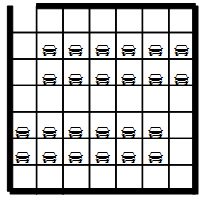
Автостоянка в Цветочном городе представляет собой прямоугольник \(N\times M\) клеток, в каждую из которых можно поставить машину. Стоянка обнесена забором, одна из сторон угловой клетки удалена (это ворота). Машина ездит по дорожке шириной в одну клетку. Незнайку попросили разместить как можно больше машин на стоянке таким образом, чтобы любая машина могла выехать, когда все прочие стоят. Например, на рисунке справа показано, как можно расположить 24 машины на стоянке размером \(7\times 7\). Помогите Незнайке решить эту задачу.
Во входном файле записано два натуральных числа N и M, не превосходящие 7.
Выведите в выходной файл единственное число: максимальное количество машинок, которое можно расставить на стоянке данного размера.
1 3
1
2 2
2
Поле размером \(N\times M\) клеток заполнено целыми числами. Требуется найти на поле клетку, из которой волна, запущенная не более чем на \(K\) итераций, покроет площадь с максимальной суммой расположенных на ней чисел.
Пример распространения волны для поля размером \(5\times 4\). Волна запущена из клетки (3, 3) и была остановлена после трех итераций. Белые клетки – клетки, не покрытые волной, серые и черные – клетки, покрытые волной. Клетки, покрытые волной на последней итерации, отмечены серым цветом.
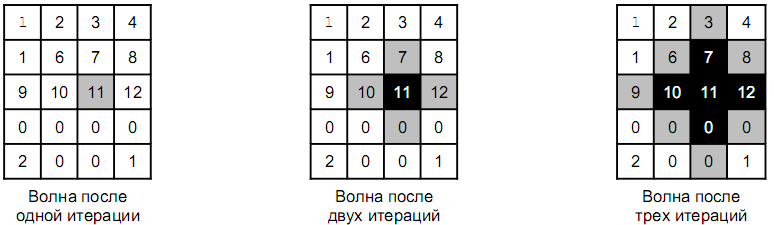
В первой строке входного файла содержатся три целых числа через пробел \(N\), \(M\) и \(K\) (\(1 \leq N, M \leq 100\), \(1 \leq K \leq N + M\)). Следующие \(N\) строк содержат по \(M\) чисел, каждое из которых не превосходит \(10000\) по абсолютной величине.
Выведите четыре числа \(R\), \(C\), \(P\) и \(S\), где \(R\) – номер строки, \(C\) – номер столбца, из которых следует запустить волну, \(P\) – количество итераций распространения волны, \(S\) – максимальная сумма чисел, покрытых волной. Если существует несколько вариантов ответа, то вывести любой, в котором число \(P\) минимально. \(1 \leq P \leq K\).
Решение, верно работающее при \(N, M \leq 15\) будет получать 50 баллов. Эти баллы выставляются при прохождении всех тестов группы. В оставшихся тестах \(N, M \leq 100\), эта группа оценивается при прохождении всех тестов группы.
5 4 3 1 2 3 4 1 6 7 8 9 10 11 12 0 0 0 0 2 0 0 1
3 3 3 66
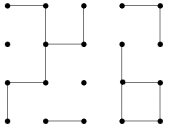 Печатной схемой называется плоская поверхность содержащей узлы и перемычки, соединяющие пары узлов. Мы будем рассматривать печатные схемы специального вида, где все узлы расположены в узлах прямоугольной сетки, а перемычки (вертикальные или горизонтальные) соединяют пары соседних узлов. Печатная схема называется связной, если любые два узла соединены друг с другом последовательностью перемычек. На вход дается печатная схема, где некоторые соседние узлы уже соединены перемычками. К ней необходимо добавить некоторое количество перемычек таким образом, чтобы схема стала связной. Стоимость вертикальной перемычки – 1, а горизонтальной – 2.
Печатной схемой называется плоская поверхность содержащей узлы и перемычки, соединяющие пары узлов. Мы будем рассматривать печатные схемы специального вида, где все узлы расположены в узлах прямоугольной сетки, а перемычки (вертикальные или горизонтальные) соединяют пары соседних узлов. Печатная схема называется связной, если любые два узла соединены друг с другом последовательностью перемычек. На вход дается печатная схема, где некоторые соседние узлы уже соединены перемычками. К ней необходимо добавить некоторое количество перемычек таким образом, чтобы схема стала связной. Стоимость вертикальной перемычки – 1, а горизонтальной – 2.
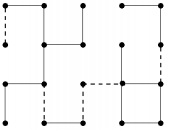 Ваша программа должна по начальной печатной схеме определить количество добавляемых перемычек, минимальную стоимость такого добавления, а также вывести сами добавляемые перемычки.
Ваша программа должна по начальной печатной схеме определить количество добавляемых перемычек, минимальную стоимость такого добавления, а также вывести сами добавляемые перемычки.
Первая строка входного файла содержит два натуральных числа \(N\) и \(M\) – количество строк (\(1 \leq N \leq 100\)) и количество столбцов (\(1 \leq M \leq 100\)) соответственно. Каждый узел определяется своими координатами, нумерация начинается с верхнего левого угла (координаты (\(1\), \(1\))). Далее дается описание решетки в виде \(N\) строк по \(M\) чисел. Каждое число обозначает связь узла (\(i\), \(j\)) с узлами (\(i+1\), \(j\)) и (\(i\), \(j+1\)) в следующем формате: \(0\) – узел (\(i\), \(j\)) не соединен ни с одним из узлов (\(i+1\), \(j\)) и (\(i\), \(j+1\)). \(1\) – узел (\(i\), \(j\)) соединен только с узлом (\(i+1\), \(j\)) \(2\) – узел (\(i\), \(j\)) соединен только с узлом (\(i\), \(j+1\)) \(3\) – узел (\(i\), \(j\)) соединен и с узлом (\(i+1\), \(j\)), и с узлом (\(i\), \(j+1\)).
Первая строка должна содержать два числа \(K\) и \(V\) – количество добавленных перемычек и стоимость добавления соответственно. Каждая из следующих \(K\) строк должна содержать описание добавленной перемычки в формате \(i\), \(j\), \(d\), где (\(i\), \(j\)) – координаты начального узла, а \(d\) может принимать значения \(1\) или \(2\). \(d = 1\) обозначает, что соединены узлы (\(i\), \(j\)) и (\(i+1\), \(j\)), \(d = 2\) – узлы (\(i\), \(j\)) и (\(i\), \(j+1\)). Если решений несколько – выведите любое из них.
4 5 2 1 1 2 1 0 3 0 1 0 3 0 0 3 1 0 2 0 2 0
5 6 1 1 1 2 3 1 3 3 1 4 3 2 2 5 1
Известны первые \(k\) членов последовательности – \(a_1, a_2, \dots, a_k\) (\(0 \leq a_i \leq 9\), где \(i = 1, 2, \dots, k\)). Другие члены последовательности вычисляются по следующему правилу: \(a_i = \sum_{j=i-k}^{i-1}a_j\), то есть каждый следующий член равен сумме \(k\) предыдущих. Необходимо найти последние \(r\) цифр числа \(a_n\).
В первой строке входного файла находятся \(3\) целых числа – \(k\), \(n\) и \(r\) (\(1 \leq k \leq 20\), \(1 \leq n \leq 10^{18}\), \(1 \leq r \leq 9\)). В следующей строке находится \(k\) чисел – \(a_1, a_2, \dots, a_k\).
Первой строкой выходного файла выведите \(r\) цифр числа \(a_n\). Ведущие нули следует опустить.
1. Тесты, в которых \(r = 1\), будут оцениваться 75 баллами:
1.1 Тесты, в которых \(n<10^6\), будут оцениваться 25 баллами.
1.2 Тесты, в которых \(n \geq 10^6\), будут оцениваться 50 баллами:
1.2.1 Тесты, в которых \(k < 7\), будут оцениваться 30 баллами.
1.2.2 Тесты, в которых \(6 < k < 11\), будут оцениваться 20 баллами.
2. Тесты, в которых \(r > 1\), будут оцениваться 25 баллами.
2 5 1 1 2
8
1 100001 1 5
5
После объявления “проходных баллов” на всероссийскую олимпиаду по информатике, один большой начальник позвонил одному из руководителей команды г. Москвы, чтобы узнать, сколько же школьников поедет на олимпиаду по информатике и сколько будут стоить авиабилеты для всей команды. Чтобы не пугать большого начальника, руководитель команды не стал называть конкретное число, а уклончиво ответил, что количество школьников в команде дает остаток 1 при делении на 2, 3, 4, 5 и 6. Но поскольку большой начальник был математиком, то, зная, что школьников в команде не меньше 10 и не больше 100, он сразу же догадался, что в команде ровно 61 школьник.
Вам известны остатки от деления некоторого числа N на числа 2, 3, ..., K. Найдите наименьшее натуральное N, которое обладает таким свойством.
Первая строка входного файла содержит натуральное число K (2≤K≤20). Дальше идет K-1 строка, содержащая остатки от деления некоторого натурального числа N на числа 2, 3, ..., K.
Выведите наименьшее натуральное число N, обладающее таким свойством.
6 1 1 1 1 1
1