#3812

Сортирующие башни

Темы: [Рекурсия] [Python]

Первоначально все диски лежат на стержне номер 1. Переместите диски с нечетными номерами на стержень номер 2, а с четными номерами - на стержень номер 3.

Вам не нужно находить минимальное решение, но количество совершенных перемещений не должно быть больше 200000, при условии, что количество дисков не превосходит 10.

Входные данные

Вводится натуральное число - количество дисков.

Выходные данные

Выведите ответ на задачу.

Примеры

Входные данные

Выходные данные

1 1 2
2 1 3

Входные данные

Выходные данные

#3813

Обменные башни

Темы: [Рекурсия] [Python]

Как и в предыдущих задачах, дано три стержня, на первом из которых надето $n$ дисков различного размера. Необходимо их переместить на стержень 3 по следующим правилам:

Самый маленький диск (номер 1) можно в любой момент переложить на любой стержень. Перемещение диска номер 1 со стержня a на стержень b будем обозначать 1 a b.

Можно поменять два диска, лежащих на вершине двух стержней, если размеры этих дисков отличаются на 1. Например, если на вершине стержня с номером a лежит диск размером 5, а на вершине стержня с номером b лежит диск размером 4, то эти диски можно поменять местами. Такой обмен двух дисков будем обозначать 0 a b (указываются номера стержней, верхние диски которых обмениваются местами).

Для данного числа дисков $n$, не превосходящего 10, найдите решение головоломки. Вам не нужно находить минимальное решение, но количество совершенных перемещений не должно быть больше 200000.

Входные данные

Вводится натуральное число - количество дисков.

Выходные данные

Выведите ответ на задачу.

Примеры

Входные данные

Выходные данные

1 1 3
0 1 3
1 1 3

Входные данные

Выходные данные

1 1 3

#3814

Фишки

Темы: [Рекурсия] [Python]

Дана полоска из клеток, пронумерованных от 1 до N слева направо. Разрешено снимать или ставить фишку на клетку с номером 1 или на клетку, следующую за самой левой из установленных фишек. Изначально полоска пуста. Нужно разместить фишки во всех клетках.

Входные данные

Программа получает на вход количество клеток в полоске $N$ $(1\le N\le 10)$.

Выходные данные

Программа должна вывести последовательность номеров клеток, с которыми совершается действие. Если фишка снимается, то номер клетки должен выводиться со знаком минус. Количество действий не должно превышать $10^4$. Если существует несколько возможных решений задачи, то разрешается вывести любое.

Тесты к этой задаче закрытые.

Ввод	Вывод
3	1 2 -1 3 1

#3815

Небоскреб

Темы: [Рекурсия] [Python]

В небоскребе $n$ этажей. Известно, что если уронить стеклянный шарик с этажа номер $p$, то шарик разобьется, и если уронить шарик с этажа номер $p+1$, то он тоже разобьется. Также известно, что при броске с последнего этажа шарик всегда разбивается.

Вы хотите определить минимальный номер этажа, при падении с которого шарик разбивается. Для проведения экспериментов у вас есть два шарика. Вы можете разбить их все, но в результате вы должны абсолютно точно определить этот номер.

Определите, какого числа бросков достаточно, чтобы заведомо решить эту задачу.

Входные данные

Программа получает на вход количество этажей в небоскребе $n$

Выходные данные

Требуется вывести наименьшее число бросков, при котором можно всегда решить задачу.

Тесты к этой задаче закрытые.

Примечание

Комментарий к первому примеру. Нужно бросить шарик со 2-го этажа. Если он разобъется, то бросим второй шарик с 1-го этажа, а если не разобъется - то бросим шарик с 3-го этажа.

Подсказки.
1. Как следует действовать, если шарик был бы только один?
2. Пусть шариков два и мы бросили один шарик с этажа номер $k$. Как мы будем действовать в зависимости от того, разобъется ли шарик или нет?
3. Пусть f(n) - это минимальное число бросков, за которое можно определить искомый этаж, если бы в небоскребе было n этажей. Выразите f(n) через значения f(a) для меньших значений a.

Примеры

Входные данные

Выходные данные

Входные данные

Выходные данные

#3816

Замок

Темы: [Условный оператор (if)]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Муниципальный этап, Москва, 2011, Задача A ]

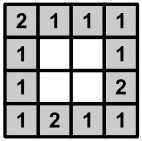
Замок имеет форму большого квадрата, составленного из N × N маленьких квадратиков. Внешние квадратики являются башнями, именно они играют основную роль в защите замка от неприятеля. Например, если замок имеет размер 4 × 4, то у него 12 башен (смотрите второй рисунок, башни на нем выделены серым цветом).

Замок охраняет K полков, которые необходимо разместить по башням. В одной башне можно разместить несколько полков, но при этом в каждой башне должен находиться хотя бы один полк, иначе неприятель легко захватит эту башню. Если все башни защищены, то неприятель выбирает для атаки одну из четырех сторон замка, которую защищает наименьшее число полков (то есть суммарное число полков во всех башнях данной стороны квадрата минимально).

Определите, как нужно разместить полки для наилучшей защиты замка.

Входные данные

Первая строка входных данных содержит число N — размер замка (2 ≤ N ≤ 100). Вторая строка входных данных содержит число K — количество полков, охраняющих замок (0 ≤ K ≤ 100).

Выходные данные

Выведите единственное число — количество полков на наименее укрепленной стороне замка при наилучшем размещении полков. Если имеющихся полков недостаточно для защиты всех башен, выведите число 0.

Примеры тестов

Входные данные

2
5

Выходные данные

Входные данные

4
15

Выходные данные

Примечание

В первом примере башни четыре, а полков пять, поэтому на одну из башен можно поставить два полка, но все равно найдется сторона, которую защищает всего два полка.

Во втором примере можно расположить полки так, что каждую сторону будет защищать 5 полков. Защитить каждую сторону не менее, чем шестью полками не удастся.

$\text{[math]}$ $\text{[math]}$