Темы --> Информатика
    Язык программирования(952 задач)
    Алгоритмы(1657 задач)
    Структуры данных(279 задач)
    Интерактивные задачи(17 задач)
    Другое(54 задач)
---> 2656 задач <---
Источники
    Личные олимпиады(938 задач)
    Командные олимпиады(684 задач)
Страница: << 418 419 420 421 422 423 424 >> Отображать по:
#111227
Ордынское войско
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes

Готовясь к бою, хан Гирей пронумеровал всех воинов своего войска натуральными числами от 1 до N. Поскольку воины умеют сражаться, но не умеют считать, при любом построении в шеренгу они выстраиваются в произвольном порядке. Одного или несколько воинов, стоящих в шеренге, будем называть отрядом. Отряд назовем правильным, если номера этих воинов в том порядке, в котором они стоят в шеренге, образуют упорядоченную по возрастанию последовательность чисел. Среди всех правильных отрядов хан Гирей выбирает ударный отряд – самый большой по количеству воинов. Так, в шеренге 1 3 2 4 из четырех воинов ударными являются отряды 1 3 4 и 1 2 4, а отряд 1 4 – один из правильных, но не ударный. Некоторые воины являются личными телохранителями хана Гирея. Требуется составить программу, определяющую количество таких шеренг, в которых телохранители хана образуют ударный отряд.

Входные данные

В первой строке входного файла задано натуральное число N – общее количество воинов (1 ≤ N ≤ 15). Во второй строке задано натуральное число K – количество телохранителей хана (1 ≤ K ≤ N). В третьей строке через пробел указаны K различных натуральных чисел, не превосходящих N, – номера телохранителей хана в порядке возрастания.

Выходные данные

Выходной файл должен содержать единственное число – количество различных расстановок всех воинов в шеренгу так, чтобы все телохранители хана были ударным отрядом в каждой из таких расстановок.

Примечание

В первом примере войско состоит из пяти воинов. Ударный отряд должен состоять из трех воинов с номерами 1, 3 и 4. Этому условию удовлетворяют следующие 11 шеренг: (1, 3, 2, 5, 4), (1, 3, 5, 2, 4), (1, 3, 5, 4, 2), (1, 5, 3, 2, 4), (1, 5, 3, 4, 2), (2, 1, 3, 5, 4), (2, 1, 5, 3, 4), (2, 5, 1, 3, 4), (5, 1, 3, 2, 4), (5, 1, 3, 4, 2), (5, 2, 1, 3, 4).

Данная задача содержит семь подзадач. Для оценки каждой подзадачи используется своя группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы успешно пройдены.

  1. (оценивается в 40 баллов) 1 ≤ N ≤ 8.

  2. (оценивается в 10 баллов) 9 ≤ N ≤ 10.

  3. (оценивается в 10 баллов) N = 11.

  4. (оценивается в 10 баллов) N = 12.

  5. (оценивается в 10 баллов) N = 13.

  6. (оценивается в 10 баллов) N = 14.

  7. (оценивается в 10 баллов) N = 15.

Примеры
Входные данные
5
3
1 3 4
Выходные данные
11
Входные данные
3
3
1 2 3
Выходные данные
1
Входные данные
1
1
1
Выходные данные
1
#111234
Наивный НОД
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Найдите НОД двух чисел.

Входные данные

Вводятся два натуральных числа, не превосходящих 10 000, разделенные пробелом.

Выходные данные

Выведите одно число - их наибольший общий делитель.

Примеры
Входные данные
2 4
Выходные данные
2
#111236
aliens
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Мирко большой фанат различных узоров на полях, в первую очередь странных кругов предположительно инопланетного происхождения. Одной летней ночью он решил создать свой собственный узор на поле своей бабушки. Так как Мирко патриот своей родной Хорватии, то он решил, что узор на поле будет в форме хорватского герба, который, как известно, представляет собой шахматную доску 5 на 5 c 13 красными и 12 белыми квадратами.

Поле бабушки Мирко разделено на \(N\) рядов по \(N\) клеток в каждом. Левый нижний угол поля обозначается координатами \((1, 1)\), правый верхний - координатами \((N, N)\).

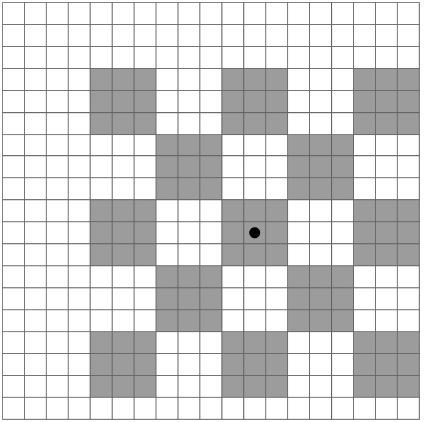
Мирко решил выкосить траву только на тех участках, которые соответствуют красным полям на шахматной доске. Он выбрал нечетное число \(M \geq 3\) и так выкосил траву на поле, что каждый квадрат на шахматной доске соответствует квадрату размером \(M \times M\) клеток на поле, и шахматная доска целиком умещается на поле.

На рисунке (см. английскую версию условия) показан пример поля для \(N = 19\) и \(M = 3\). Клетки, на которых трава была выкошена, отмечены серым. Центр узора имеет координаты \((12, 9)\) и отмечен черной точкой

После того, как Мирко пошел спать, его творение привлекло внимание настоящих инопланетян! Они летают высоко вверху над полем в космическом корабле и исследуют узор с помощью прибора. Этот прибор может лишь определить, есть ли в определенной клетке трава или нет.

Пришельцы нашли одну клетку с выкошенной травой и теперь хотят найти центральную клетку узора Мирко. Они не знают размера узора \(M\).

Входные данные

Напишите программу, которая по размеру поля \(N\) (\(1 \leq N \leq 2\,000\,000\,000\)), координатам некоторой клетки с выкошенной травой \((X_0, Y_0)\) и способности взаимодействовать с инопланетным устройством, найдет центральную клетку узора Мирко

На каждом тесте устройство не может быть запущено более 300 раз

Это интерактивная задача. Ваша программа может взаимодействовать с устройством инопланетян, используя стандартный вывод и считывая данные, передаваемые устройством со стандартного ввода

  • При запуске программы ей будут введены разделенные пробелом числа \(N\), \(X_0\), \(Y_0\).
  • Для того, чтобы узнать есть ли трава в клетке \((X, Y)\) выведите на стандартный поток вывода строку "examine \(X\) \(Y\)". Если координаты \((X, Y)\) не будут находиться внутри поля или вы запустите устройство более 300 раз, то космический корабль потеряет управление и врежется в землю. Вы же в этом случае получите 0 баллов за тест.
  • Устройство поместит в ваш стандартный поток ввода строку "true", если трава в указанной клетке выкошена и "false" в противном случае.
  • Когда программа обнаружит центральную клетку, она должна вывести строку "solution \(X_c\) \(Y_c\)" на стандартный поток вывода. Выполнение вашей программы в этот момент будет автоматически завершено.

      • Для корректной работы вашей программы не забывайте вызывать функцию "flush" после каждого вывода данных. Её заменяет endl в С++, print в Python, writeln в Pascal.

Пример диалога
> 20 4 9
< examine 2 9
> false
< examine 3 9
> true
< examine 6 9
> false
< examine 5 9
> true
< examine 4 3
> true
< examine 2 3
> false
< examine 3 3
> true
< examine 3 1
> false
< examine 3 2
> true
< solution 10 9
#111240
Переворот
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Дан массив. Надо научиться обрабатывать два типа запросов.

* 1 L R - перевернуть отрезок \([L,\,R]\)

* 2 L R - найти минимум на отрезке \([L,\,R]\)

Входные данные

Первая строка файла содержит два числа \(n\), \(m\). (\(1 \le n,m \le 10^5\)) Во второй строке находится \(n\) чисел \(a_i\) (\(1 \le a_i \le 10^9\)) — исходный массив. Остальные \(m\) строк содержат запросы, в формате описанном в условии. Для чисел \(L\), \(R\) выполняется ограничение (\(1 \le L \le R \le n\)).

Выходные данные

На каждый запрос типа 2, во входной файл выведите ответ на него, в отдельной строке.

Примеры
Входные данные
10 7
5 3 2 3 12 6 7 5 10 12
2 4 9
1 4 6
2 1 8
1 1 8
1 8 9
2 1 7
2 3 6
Выходные данные
3
2
2
2
#111243
class LinEquation
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
256 megabytes

Реализуйте class LinEquation

Страница: << 418 419 420 421 422 423 424 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест