#111403

Квадратный корень и квадратный квадрат

Темы: [Бинарный поиск значения функции]

Найдите такое число $x$, что $x^2 + \sqrt{x} = C$, с точностью не менее $6$ знаков после точки.

Входные данные

В единственной строке содержится вещественное число $1.0 \le C \le 10^{10}$.

Выходные данные

Выведите одно число — искомый $x$.

Примеры

Входные данные

2.0000000000

Выходные данные

1.000000000

Входные данные

18.0000000000

Выходные данные

4.000000000

#111404

Мутанты

Темы: [Бинарный поиск в массиве]

Уже долгое время в Институте Искусств, Мутантов и Информационных Технологий разводят милых разноцветных зверюшек. Для удобства каждый цвет обозначен своим номером, всего цветов не более $10^9$. В один из прекрасных дней в питомнике случилось чудо: все зверюшки выстроились в ряд в порядке возрастания цветов. Пользуясь случаем, лаборанты решили посчитать, сколько зверюшек каждого из запрошенных цветов живет в питомнике, и, по закону жанра, попросили вас написать программу, которая поможет им в решении этой нелегкой задачи.

Входные данные

В первой строке входного файла содержится единственное число $N$ ($0 \le N \le 10^5$) — количество зверюшек в Институте. В следующей строке находятся $N$ упорядоченных по неубыванию неотрицательных целых чисел, не превосходящих $10^9$ и разделенных пробелами — их цвета. В третьей строке файла записано число $M$ ($1 \le M \le 100\,000$) — количество запросов вашей программе, в следующей строке через пробел записаны $M$ целых неотрицательных чисел (не превышающих $10^9+1$).

Выходные данные

Выходной файл должен содержать $M$ строчек. Для каждого запроса выведите число зверюшек заданного цвета в питомнике.

Примеры

Входные данные

10
1 1 3 3 5 7 9 18 18 57
5
57 3 9 1 179

Выходные данные

#111405

Ацтекская пирамида

Темы: [Формула]

Император ацтеков Куитлауак собирается построить пирамиду в свою честь. Эта пирамида должна быть выше, чем все предыдущие.

Ацтекская пирамида состоит из каменных блоков. Каждый блок это куб размерами 1 × 1 × 1. Куитлауак располагает первый блок на земле в процессе церемонии закладки пирамиды. Каждый следующий блок должен иметь общую грань с каким-нибудь из предыдущих блоков.

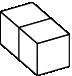
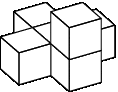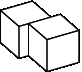
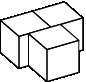
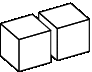
Правильные расположения блоков: $\text{[math]}$ $\text{[math]}$ Неправильные расположения блоков: $\text{[math]}$ $\text{[math]}$ $\text{[math]}$

Блок считается устойчивым, если он стоит на земле или на блоке, каждая грань которого соседствует с другим блоком или с землей. Чтобы пройти испытание временем, пирамида должна быть устойчивой, то есть все её блоки должны быть устойчивыми.

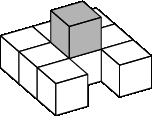
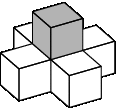
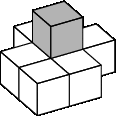
Устойчивые блоки: 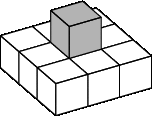$\text{[math]}$ $\text{[math]}$ $\text{[math]}$ Неустойчивые блоки: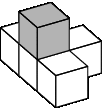 $\text{[math]}$ $\text{[math]}$

Куитлауак просит вас определить высоту самой высокой пирамиды, которую можно построить из имеющихся в наличии блоков.

Входные данные

Единственная строка входного файла содержит одно целое число n — количество имеющихся в наличии блоков, считая заложенный императором (1 ≤ n ≤ 10⁹).

Выходные данные

Выведите одно целое число — высоту самой высокой пирамиды, которую можно построить из имеющихся в наличии блоков.

Примеры тестов

Входные данные

Выходные данные

Входные данные

Выходные данные

Входные данные

Выходные данные

#111406

Морской бой

Темы: [Двумерные массивы] [Конструктив]

Вы занимаетесь компьютерной безопасностью. Недавно один из ваших клиентов разработал новый тест, предназначенных для того, чтобы отличить человека от программы. Ваша задача — протестировать его эффективность.

Тест основан на игре «Морской бой». Эта игра проводится на клетчатом поле размером 10 × 10 клеток. Перед началом игры вы должны разместить десять кораблей на этом поле. Каждый корабль задается числом последовательных клеток, расположенных горизонтально или вертикально. Вы должны разместить один четырехклеточный корабль, два трехклеточных, три двухклеточных и четыре одноклеточных корабля. Никакие два корабля не могут иметь общую или соседние по стороне или углу клетки.

После того, как все корабли расставлены, тест продолжается в течение некоторого количества раундов. В каждом раунде выбирается одна клетка, по которой производится стрельба. Корабль тонет, если по каждой его клетке пришлось не менее одного попадания. Тест заканчивается, когда все корабли утонули.

Назовем сложностью расположения кораблей количество раундов, которое потребуется для того, чтобы завершить тест. Идея теста в том, что люди будут создавать более сложные расположения, чем программы.

Вы же выяснили, что порядок, в котором производится стрельба по клеткам, заранее задан, по каждой клетке стреляют ровно один раз. Теперь вам нужно написать программу, которая создает самое сложное расположение кораблей.

Входные данные

Входной файл состоит из десяти строк, каждая из которых содержит десять чисел. Каждое число обозначает номер раунда, в котором по соответствующей клетке будет вестись стрельба. Все числа различны и лежат в диапазоне 1... 100.

Выходные данные

Выведите какое-нибудь оптимальное расположение кораблей для данного порядка стрельбы. Пустые клетки должны быть обозначены точкой ('.'), занятые клетки должны быть обозначены решёткой ('#').

Примеры тестов

Входные данные

1 2 3 4 5 6 7 8 9 10
36 37 38 39 40 41 42 43 44 11
35 64 65 66 67 68 69 70 45 12
34 63 84 85 86 87 88 71 46 13
33 62 83 96 97 98 89 72 47 14
32 61 82 95 100 99 90 73 48 15
31 60 81 94 93 92 91 74 49 16
30 59 80 79 78 77 76 75 50 17
29 58 57 56 55 54 53 52 51 18
28 27 26 25 24 23 22 21 20 19

Выходные данные

...####...
..........
#....##...
#.#.....#.
........#.
...###....
.#........
........#.
..#.....#.
.....#..#.

#111408

Метрострой

Темы: [Элементарная геометрия]

После постройки станции метро Адмиралтейская, правительство Санкт-Петербурга решило построить по-настоящему глубокую станцию, которая будет самой глубокой в мире. Она будет расположена на глубине d метров под землей! Станция будет построена прямо под Смольным собором и будет предназначена для использования только должностными лицами. Департамент городского развития использует свою систему координат для этого проекта. Центром этой системы координат является Смольный собор и третья координата обозначает глубину. Соответственно, новая станция будет иметь координаты (0, 0, d).

Из-за соображений безопасности вестибюль станции должен быть расположен снаружи Смольного монастыря, в точке (x, y). Ваша задача — помочь правительству с постройкой эскалаторов. Станция будет использовать инновационные эскалаторы, которые идут вниз под углом 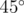$\text{[math]}$ . Возможна постройка промежуточного подземного вестибюля и двух эскалаторов. Вам даны x, y и d, найдите координаты промежуточного вестибюля. Заметьте, что вы не можете ничего строить на глубине, большей чем d, так что промежуточный вестибюль должен быть не глубже, чем основная станция.

Входные данные

Единственная строка входного файла содержит три целых числа: x, y и d — координаты вестибюля станции в системе Департамента городского развития и глубина станции ( - 10 000 ≤ x, y ≤ 10 000; (x, y) ≠ (0, 0); 106 ≤ d ≤ 10 000).

Выходные данные

Выведите три числа с точностью не менее, чем 10 знаков после десятичной точки: координаты промежуточного вестибюля в системе координат Департамента городского развития.

Если невозможно построить эскалаторы, выведите "Impossible". Если промежуточный вестибюль не требуется, выведите "Single staircase".

Примеры тестов

Входные данные

0 100 300

Выходные данные

0.0 200.0 100.0

Входные данные

300 400 500

Выходные данные

Single staircase

Входные данные

400 400 500

Выходные данные

Impossible