В одном курином ресторане можно купить:

1. 1 ножку  + 1 крыло,
2. 1 ножку  + 1 бедро,
3. 1 бедро,
4. 2 крыла,
5. 3 крыла.

Требуется определить, можно ли купить ровно k крыльев, n ножек и b бедер

Одно из известных развлечений со словами — составление палиндромов. Палиндромом называется предложение, которое, после удаления из него всех пробелов и знаков препинания, читается одинаково справа налево и слева направо. Создатели одного известного текстового редактора пишут новую версию модуля для проверки орфографии. Они хотят реализовать возможность вывода подсказки для пользователя на тот случай, если он допустил опечатку при наборе какого-нибудь палиндрома. Конечно же, они решили обратиться именно к вам.

Более точно, по заданной строке нужно определить, может ли она быть результатом замены, удаления или добавления одного символа в некотором палиндроме. При этом строчные и прописные латинские буквы не различаются, а все остальные символы должны игнорироваться.

Большое количество соревнований по разным видам спорта проводится по так называемой "олимпийской системе". В простейшем варианте она состоит в следующем. В турнире участвуют N = 2^k игроков. Они получают номера от 1 до N, и в первом круге игрок 1 играет с игроком 2, игрок 3 с игроком 4 и т. д., игрок (N - 1) — с игроком N. Проигравшие в каждой паре выбывают из соревнований, а победители проходят во второй круг. Там победитель первой пары (т. е. игрок 1 или игрок 2) играет с победителем второй пары и т. д. Таким образом, в первом круге участвуют N = 2^k игроков, во втором круге — 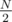= 2^k - 1 и т. д., в финале участвуют два игрока.

Серьезной проблемой является то, что некоторые сильные игроки могут встретиться между собой уже в одном из первых кругов, в результате чего некоторые сильные участники могут рано выбыть из борьбы, в то время как другие, менее сильные участники, могут пройти намного выше, если им повезет с соперниками. Для борьбы с этим эффектом применяется так называемый “рассев” игроков, когда начальная нумерация участников не является полностью случайной, и вероятность “везения”/”невезения” с соперниками резко уменьшается.

В этой задаче вам нужно будет написать программу, находящую в некотором смысле оптимальный “рассев” игроков. Для этого рассмотрим следующую модель. Предположим, что участников можно упорядочить по силе так, что более сильный игрок всегда будет выигрывать у более слабого. В таком случае по изначальному “рассеву” игроков дальнейший ход соревнований будет однозначно определен. Тогда в качестве критерия оптимальности рассева” можно потребовать выполнение следующих условий: в финале играют двое сильнейших игроков, в полуфиналах играют четверо сильнейших игроков, и т. д.: в каждом круге играют только сильнейшие игроки (т. е. если в каком-то круге m мест, то в этом круге должны участвовать m сильнейших игроков). Вам дано N. Найдите любой оптимальный рассев N игроков.

Для заданного натурального N найти последнюю ненулевую цифру числа N!.

Зачет проводится в аудитории, в которой стоит один большой круглый стол, за которым ровно N мест; студентов в группе тоже ровно N. За время семестра преподаватель успел выделить несколько пар студентов, которые, по его мнению, могут списывать друг у друга, при этом каждый студент входит не более чем в одну такую пару. Теперь он хочет придумать такую рассадку для студентов, чтобы они все решали задачи самостоятельно.

Преподаватель считает, что списывать сложнее всего, если тот, у кого списывают, находится на расстоянии ровно L от того, кто списывает. Таким образом, преподаватель хочет рассадить студентов так, чтобы между каждыми двумя студентами, которые могут списывать друг у друга, сидело бы ровно L - 1 других студентов. Помогите преподавателю найти такую рассадку. Примечание. Ясно, что в зависимости от того, с какого именно из двух студентов начинать считать, и в зависимости от того, в какую сторону считать, получится разное количество человек, сидящих между ними. Преподавателю требуется лишь, чтобы для каждой пары, начиная с хотя бы какого-нибудь из этих двух студентов, хотя бы в какую-нибудь сторону до другого насчитывался бы ровно L - 1 студент.