Темы --> Информатика
    Язык программирования(952 задач)
    Алгоритмы(1657 задач)
    Структуры данных(279 задач)
    Интерактивные задачи(17 задач)
    Другое(54 задач)
---> 2656 задач <---
Источники
    Личные олимпиады(938 задач)
    Командные олимпиады(684 задач)
Страница: << 444 445 446 447 448 449 450 >> Отображать по:
#111706
Подстрока
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
128 megabytes

Помимо известной операции сложения двух строк, введем операцию умножения целого неотрицательного числа a на строку s, означающую повторение строки s a раз (при a = 0 мы получаем пустую строку).

Даны строки x и z длиной не более 250 символов. Требуется найти такую минимально возможную по длине строку y, что для некоторого натурального i и целого неотрицательного a, будет выполняться следующее: подстрока(ax + y, i, k) = z, здесь i означает, с какого символа берется подстрока, k — длина подстроки строки ax + y. Нумерация символов в строке начинается с 1.

Входные данные

В первой строке вводится строка x, во второй строке вводится строка z. Каждая строка состоит только из маленьких латинских букв и имеет длину не более 250 символов.

Выходные данные

Выведите минимальную по длине искомую строку y.

Примечание

В первом тесте ответ — пустая строка, a = 2, i = 2.

Во втором тесте a = 1, i = 2.

В третьем тесте a = 0, i = 1.

Примеры
Входные данные
mama
amamam
Выходные данные
Входные данные
mam
amamam

Выходные данные
amam

Входные данные
ura
mura

Выходные данные
mura


                            
                                


                        

                    

                    

                        

                            

                                #111707
                            

                            

                                Художник
                            

                              
                
                            

                                
                                


                                

                            


                        

                        

                                

                                

                                    

                                        
ограничение по времени на тест

                                        1.0 second;
                                    
                                        
ограничение по памяти на тест

                                        128 megabytes
                                    

                                

                            
                            
Известный художник решил написать новый шедевр. После многих дней усердной работы он захотел исследовать свое творение. Художник вспомнил, что картина писалась следующим образом. Сначала был взят белый холст, имеющий форму прямоугольника шириной w и высотой h. Затем художник нарисовал на этом холсте n прямоугольников с координатами углов (x1i;y1i), (x1i;y2i), (x2i;y2i), (x2i;y1i).
Помогите художнику определить площадь незакрашенной части холста.
Входные данные
Первая строка содержит два целых числа w и h (1 ≤ w;h ≤ 100) — ширину и высоту холста соответственно. Вторая строка входного файла содержит целое число n (0 ≤ n ≤ 5000) — количество прямоугольников. Следующие n строк содержат информацию о прямоугольниках. (i + 2)-ая строка содержит четыре целых числа x1i; y1i, x2i; y2i (0 ≤ x1i ≤ x2i ≤ w, 0 ≤ y1i ≤ y2i ≤ h).
Выходные данные
Выведите ответ на задачу.

                            
Примеры
Входные данные
5 5
2
1 1 3 3
2 2 4 4

Выходные данные
18

Входные данные
6 7
3
0 0 5 5
1 1 4 4
2 2 3 3

Выходные данные
17


                            
                                


                        

                    

                    

                        

                            

                                #111708
                            

                            

                                Часы
                            

                              
                
                            

                                
                                


                                

                            


                        

                        

                                

                                

                                    

                                        
ограничение по времени на тест

                                        1.0 second;
                                    
                                        
ограничение по памяти на тест

                                        128 megabytes
                                    

                                

                            
                            
Петя очень любит наблюдать за электронными часами. Он целыми днями смотрел на часы и считал, сколько раз встречается каждая цифра. Через несколько месяцев он научился по любому промежутку времени говорить, сколько раз на часах за это время встретится каждая цифра, и очень гордился этим.
Вася решил проверить Петю, но он не знает как решать эту задачу. Вася попросил вас помочь ему. Напишите программу, решающую эту задачу.
Входные данные
Первая и вторая строки входного файла содержат начало и конец промежутка времени соответственно. Начальное время не превосходит конечное. Время задается в формате hh : mm : ss (0 ≤ hh < 24, 0 ≤ mm < 60, 0 ≤ ss < 60). hh, mm, ss дополнены ведущими нулями до двух символов. Эти нули также учитываются при подсчете числа цифр.
Выходные данные
Выходной файл должен содержать 10 строк. В i-ой строке должно быть написано, сколько раз встречается цифра i - 1.

                            
Примеры
Входные данные
23:59:58
23:59:59

Выходные данные
0
0
2
2
0
4
0
0
1
3


                            
                                


                        

                    

                    

                        

                            

                                #111710
                            

                            

                                Дороги
                            

                              
                
                            

                                
                                


                                

                            


                        

                        

                                

                                

                                    

                                        
ограничение по времени на тест

                                        0.5 second;
                                    
                                        
ограничение по памяти на тест

                                        64 megabytes
                                    

                                

                            
                            
Мэр города Гадюкино решил проверить состояние дорог после только что проведенного капитального ремонта. Для этого он хочет проехать по каждой дороге в обоих направлениях.
Помогите мэру составить кратчайший маршрут, проходящий по каждой дороге в каждом направлении хотя бы один раз.
Входные данные
В городе Гадюкино n перекрестков и m дорог, каждая из которых соединяет два различных перекрестка. Между двумя перекрестками может быть не более одной дороги.
Известно, что по дорогам от каждого перекрестка можно доехать до любого другого.
Входной файл содержит целые числа n и m (1 ≤ n ≤ 104, 1 ≤ m ≤ 105), и далее m пар целых чисел ai и bi — номера перекрестков, которые соединяет i-я дорога.
Выходные данные
Выведите число s — минимальную длину пути и далее s + 1 число — номера перекрестков в том порядке, в котором их нужно проезжать.

                            
Примеры
Входные данные
3 3
1 2
2 3
1 3

Выходные данные
6
1 3 2 1 2 3 1 


                            
                                


                        

                    

                    

                        

                            

                                #111711
                            

                            

                                Dynamic LCA
                            

                              
                
                            

                                
                                


                                

                            


                        

                        

                            
                            
Постановка задачи о {Наименьшем общем предке} такова: дано дерево T с выделенным корнем и две вершины u и v, lca(u, v) - вершина с максимальной глубиной, которая является предком и u, и v. Например, в картинке внизу lca(8, 7) - вершина 3.
  
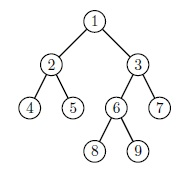
С помощью операции chroot(u) мы можем менять корень дерева, достаточно отметить u, как новый корень, и направить ребра вдоль пути от корня. Наименьшие общие предки вершин поменяются соответствующе. Например, если мы сделаем chroot(6) на картинке сверху, lca(8, 7) станет вершина 6. Получившееся дерево изображено снизу.
  
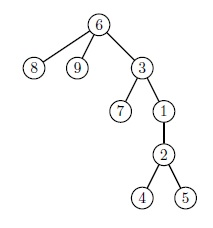
Вам дано дерево T. Изначально корень этого дерева - вершина 1. Напишите программу, которая поддерживает эти две операции: lca(u, v) и chroot(u).
Входные данные
Входной файл состоит из нескольких тестов.
Первая строка каждого теста содержит натуральное число n  — количество вершин в дереве (1 ≤ n ≤ 100 000). Следующие n - 1 строки содержат по 2 натуральных числа и описывают ребра дерева. Далее идет строка с единственным натуральным числом m — число операций —. Следующие m строк содержат операции. Строка "? u v" означает операцию lca(u, v), a строка "! u" - chroot(u). Последняя строка содержит число 0.
Сумма n для всех тестов не превосходит 100 000. Сумма m для всех тестов не превосходит 200 000.
Выходные данные
Для каждой операции "? u v" выведите значение lca(u, v). Числа разделяйте переводами строк.



  
Система оценки:

  
Система тестов состоит из двух групп:

  

  
Первая группа состоит из тестов, для которых выполняется ограничение \(n \le 100\), \(m \le 10000\). За прохождение всех тестов группы ставится 55 баллов. 

  
Вторая группа стоит из тестов, в которых нет дополнительных ограничений. За прохождение тестов этой группы и всех предыдущих тестов ставится дополнительно 45 баллов.



                            
Примеры
Входные данные
9
1 2
1 3
2 4
2 5
3 6
3 7
6 8
6 9
10
? 4 5
? 5 6
? 8 7
! 6
? 8 7
? 4 5
? 4 7
? 5 9
! 2
? 4 3
0

Выходные данные
2
1
3
6
2
3
6
2


                            

                        

                    

                

                
        

            Страница: 
                <<
                    444
                    445
                    446
                    447
                    448
                    449
                    450
                >>
            Отображать по:
            
        

    
            

        

        
    
    

    

        

            
Выбрано
:
            
Отменить
|
            
Добавить в контест