Алгоритмы(1657 задач)
Структуры данных(279 задач)
Интерактивные задачи(17 задач)
Другое(54 задач)
Последовательность ДНК любого живого существа в Берляндии представима в виде непустой строки из маленьких латинских букв. Берляндские ученые выяснили, что эволюции всех существ происходят поэтапно. На одном этапе ровно один некоторый символ последовательности ДНК заменяется ровно на два других. При этом всего бывает n допустимых замен. Замена 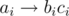 означает, что можно заменить один любой символ ai на пару символов bici. Каждая замена могла произойти неограниченное число раз.
означает, что можно заменить один любой символ ai на пару символов bici. Каждая замена могла произойти неограниченное число раз.
Говорят, что два существа, имеющие последовательности ДНК s1 и s2, могут иметь общего предка, если существует такая последовательноcть ДНК s3, что из нее в процессе эволюции могут быть получены s1 и s2, возможно за разное число этапов. По заданным s1 и s2 требуется определить, могут ли существа, имеющие такие последовательности ДНК, иметь общего предка. В случае положительного ответа требуется найти длину кратчайшей последовательноcти ДНК общего предка.
В первой строке записана непустая последовательность ДНК s1, во второй строке записана непустая последовательность ДНК s2. Длины этих строк не превосходят 50, строки содержат только маленькие латинские буквы. В третьей строке записано целое число n(0 ≤ n ≤ 50) допустимых замен. Далее следует n строк, каждая из которых описывает очередную замену в формате 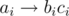 . Символы ai, bi, и ci — маленькие латинские буквы. Строки s1 и s2 могут совпадать, список замен может содержать одинаковые замены.
. Символы ai, bi, и ci — маленькие латинские буквы. Строки s1 и s2 могут совпадать, список замен может содержать одинаковые замены.
Если s1 и s2 не могут иметь общего предка, выведите -1. Иначе выведите длину кратчайшей последовательности s3, из которой могли быть получены s1 и s2.
ababa aba 2 c->ba c->cc
2
ababa aba 7 c->ba c->cc e->ab z->ea b->ba d->dd d->ab
1
Найти количество покрытий прямоугольника 2 * n фигурами в виде дощечек, каждая из которых представляет собой либо квадрат со стороной 1, либо два квадрата (2 * 1), либо “уголок” из трех квадратов:

Фигуры должны заполнять прямоугольник без промежутков.
Вводится число n(1 ≤ n ≤ 1000).
Выведите количество возможных покрытий.
2
11
Дано два списка чисел, числа в первом списке упорядочены по неубыванию. Для каждого числа из второго списка определите номер первого и последнего появления этого числа в первом списке.
В первой строке входных данных записано два числа \(N\) и \(M\) (\(1\le N, M\le 20000\)). Во второй строке записано \(N\) упорядоченных по неубыванию целых чисел — элементы первого списка. В третьей строке записаны \(M\) целых неотрицательных чисел - элементы второго списка. Все числа в списках - целые 32-битные знаковые.
Программа должна вывести \(M\) строчек. Для каждого числа из второго списка нужно вывести номер его первого и последнего вхождения в первый список. Нумерация начинается с единицы. Если число не входит в первый список, нужно вывести одно число \(0\).
10 5 1 1 3 3 5 7 9 18 18 57 57 3 9 1 179
10 10 3 4 7 7 1 2 0
Система телефонных номеров в России устроена следующим образом. Все телефонные номера имеют одну и ту же длину — M цифр. Номер состоит из двух частей: несколько первых цифр номера составляют код города, остальные цифры определяют номер абонента в пределах этого города.
В процессе развития сети коды городов регулярно меняются, при этом, коды различных городов обязательно различны. В остальном коды могут быть совершенно произвольными, в том числе код одного города может быть началом кода другого (например, код Нижнего Новгорода — 831, а код Сарова — 83130) и т. п. Если коды нескольких городов являются началом M-значного номера абонента, кодом города этого номера считается наидлиннейший из таких кодов. Так, если есть всего четыре города: Нижний Новгород, Балахна, Дзержинск и Саров с кодами, соответственно, 831, 83144, 8313 и 83130, и M = 9, то: телефоны 831123456 и 831412345 — телефоны Нижнего Новгорода, 831312345 — телефон Дзержинска, 831301234 — Сарова, а 831441234 — Балахны.
В этой задаче мы не будем учитывать различные другие ограничения на телефонные номера, существующие в реальности (например, в реальности никакой номер абонента в городе не может начинаться на 03, т. к. 03 — это телефон скорой помощи). Мы будем считать, что любой из 10M возможных M-значных номеров является допустимым телефонным номером.
Нетривиальной задачей становится задача определения, сколько всего телефонных номеров может быть выдано в каждом городе. Например, в приведённом выше примере в Балахне и Сарове могут быть выданы 10 000 телефонных номеров (все четырёхзначные номера), в Дзержинске могут быть выданы 90000 телефонных номеров — все пятизначные телефонные номера, кроме начинающихся на ноль, а в Нижнем Новгороде могут быть выданы 890 000 номеров — все шестизначные номера, кроме тех, которые начинаются на цифру 3, а также на последовательность 44.
Напишите программу, которая решит эту задачу для произвольного набора кодов городов.
На первой строке входного файла находятся два числа N и M — количество городов и длина полного телефонного номера (1 ≤ N ≤ 100 000, 1 ≤ M ≤ 9). Далее следуют N строк, в каждой из которых находится код очередного города и название города, между которыми находится ровно один пробел. Название города состоит только из заглавных и маленьких латинских букв и не превышает по длине 20 символов. Гарантируется, что в каждой из этих строк входного файла будет ровно один пробел — между кодом города и его названием.
Города во входном файле отсортированы по алфавитному порядку кодов. Гарантируется, что никакие два кода и никакие два названия города не совпадают.
В выходной файл выведите N строк. В каждой строке выведите название города и количество телефонных номеров, которые можно выдать в этом городе. Отделяйте название города и количество номеров как минимум одним пробелом. Вы также можете выводить лишние пробелы в начало и конец каждой строки; они будут игнорироваться.
Города можете выводить в произвольном порядке.
4 9 831 NizhnyNovgorod 8313 Dzerzhinsk 83130 Sarov 83144 Balakhna
Sarov 10000 Dzerzhinsk 90000 Balakhna 10000 NizhnyNovgorod 890000
Цепочкой слов длины n назовем последовательность слов w1, w2, ..., wn такую, что для 1 ≤ i ≤ n слово wi является собственным префиксом слова wi + 1.
Напомним, что слово u длины k называется собственным префиксом слова v длины l, если l > k и первые k букв слова v совпадают со словом u.
Задано множество слов S = {s1, s2, ..., sm}. Найдите максимальную длину цепочки слов, которую можно построить, используя (возможно, не все) слова этого множества.
Первая строка входного файла содержит целое число m(1 ≤ m ≤ 255). Каждая из последующих m строк содержит по одному слову из множества S.
Все слова не пусты, имеют длину, не превосходящую 255 символов, и состоят только из строчных букв латинского алфавита.
В выходной файл выведите ответ на задачу.
3 a ab abc
3
5 a ab bc bcd add
2