В городе N в ближайшее время состоится этап чемпионата мира по автогонкам среди автомобилей класса Формула-0. Поскольку специальный автодром для этих соревнований организаторы построить не успели, было решено организовать трассу на улицах города.

В городе N есть n перекрестков, некоторые пары которых соединены дорогами, движение по которым возможно в обоих направлениях. При этом любые два перекрестка соединены не более чем одной дорогой.

Трасса, на которой будут проводиться соревнования, должна быть круговой (т.е. должна начинаться и заканчиваться на одном и том же перекрестке), при этом в процессе движения по ней никакой перекресток не должен встречаться более одного раза.

На предварительном этапе подготовки оргкомитетом был создан список всех дорог города. Теперь настало время его использовать. Первый вопрос, который необходимо решить, – вопрос о существовании в городе требуемой круговой трассы (разумеется, если ответ будет отрицательным, организаторам придется в срочном порядке построить еще несколько дорог). Единственная проблема заключается в том, что у организаторов есть подозрение, что, поскольку список составлялся не очень внимательно, в нем некоторые дороги указаны больше одного раза.

Напишите программу, которая по заданному списку дорог города определит, возможна ли организация в городе требуемой круговой трассы.

Женя недавно купил себе новую соковыжималку. Теперь по утрам он и его братья и сестры пьют свежевыжатый фруктовый сок. А это, между прочим, очень полезно!

Недавно они поняли, что можно пить сок, выжатый не только из одного вида фруктов, как, например, апельсиновый, но и различные смеси, например, виноградно-яблочный.

В Жениной семье все очень любят сок, поэтому могут утром выпить не один стакан, причем разных видов сока. Например, его сестра Катя очень любит грейпфрутовый и апельсиновый соки. Женя, как наиболее технически грамотный человек, каждое утро занимается приготовлением соков.

Опишем подробнее, как работает соковыжималка. В нее загружаются фрукты, они проходят отжим в центрифуге, обезвоженная мякоть сбрасывается в отдельный резервуар, а сок попадает в специальную емкость.

Основная проблема состоит в том, что эту емкость иногда приходится мыть. Например, если после приготовления апельсинового сока, необходимо приготовить яблочный, то емкость надо мыть, иначе получится апельсиново-яблочный сок. Более формально, пусть сок A состоит из компонентов a₁, ..., a_n, а сок B – из компонентов b₁, ..., b_m. Сок B можно готовить после сока A, если любой из компонентов a_i является компонентом сока B (т.е. 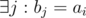). В противном случае емкость для сока надо помыть.

Женя не очень любит мыть посуду, поэтому хочет мыть емкость как можно меньшее число раз. Помогите ему.

N гостей засиделись на даче и боятся опоздать на последнюю электричку. У хозяина дачи, который остается на ночь, есть автомобиль, но в него могут сесть одновременно не более 4 человек, не считая шофера. Скорость движения автомобиля по лесной дороге – V км/ч, скорость движения пешехода – U км/ч, расстояние от дачи до железнодорожной станции – Z км, затратами времени на посадку-высадку пассажиров и разворот автомобиля можно пренебречь. За какое минимальное время все гости доберутся до станции?

Рассмотрим произвольную последовательность целых чисел. Между числами можно расставить знаки арифметических операций + или – , и таким образом получать некоторые выражения, которые принимают различные значения. Например, если взять последовательность: 17, 5,  - 21, 15, то можно получить восемь различных выражений:

Назовем последовательность делящейся на натуральное K, если + и – могут быть расставлены так, что итоговое значение выражения будет делиться на K. В приведенном примере последовательность делится на 7  (17 + 5 +  - 21 - 15 =  - 14), но не делится на 5.

Ваша задача — написать программу, определяющую делимость последовательности на целое число.