Алгоритмы(1657 задач)
Структуры данных(279 задач)
Интерактивные задачи(17 задач)
Другое(54 задач)
Вася работает подмастерьем в известной студии. Недавно ему поручили помогать молодому, но подающему большие надежды художественному декоратору заборов и изгородей Витезславу Смолокурову. Миссия эта очень ответственная, и от ее выполнения зависит Васино будущее.
Стиль Смолокурова очень необычен, а его работы пользуются большим спросом. Процесс работы разделен на два этапа. На первом этапе Вася делает заготовку — длинный забор, который состоит из набора цветных вертикальных планок. На втором этапе Витезслав приступает к работе.
Для того, чтобы придать забору более спокойный и гармоничный вид, он несколько раз производит следующую операцию: выбирает некоторый цвет и отрезок, после чего перекрашивает этот отрезок забора в выбранный цвет. По своей творческой натуре, Смолокуров может в корне менять концепцию узора по нескольку раз за час, поэтому иногда он перекрашивает одну и ту же планку несколько раз. Кроме того, Витезслав не хочет, чтобы какой-то узор повторялся слишком часто. Для того, чтобы избежать этого, он иногда проверяет, не совпадает ли один отрезок забора с другим.
Несложно догадаться, что и перекрашивание, и проверки осуществляет Вася. Работа эта не самая простая, поэтому Вася просит ему помочь хотя бы с проверками на совпадение.
Первая строка входного файла содержит одно целое число n — количество планок в заборе (1 ≤ n ≤ 100 000). Вторая строка содержит n целых чисел, разделенных пробелами — цвета соответствующих планок.
Третья строка входного файла содержит одно целое число m — количество сравнений и перекрашиваний (1 ≤ m ≤ 100 000). Следующие m строк содержат описания заданий, который Вася получает от Витезслава: четыре целых числа q, l, r и k.
В случае перекрашивания q = 0. Эта запись означает перекрашивание всех планок с l по r включительно в цвет k (1 ≤ l ≤ r ≤ n). В запросе на сравнение q = 1. Эта запись означает сравнение кусков забора длины k начиная с позиций l и r соответственно (1 ≤ l, r ≤ n - k + 1, k > 0).
Все числа во входном файле положительные и не превышают 100 000.
Выведите одну строку: для каждого запроса на сравнение выведите ‘+’ в случае совпадения соответствующих кусков забора и ‘-’ в противном случае.
7 1 2 1 3 1 2 1 3 0 4 5 2 1 3 1 2 1 3 1 3
+-
2 1 2 5 1 1 2 1 0 2 2 1 1 1 2 1 0 1 2 3 1 1 1 2
-++
Группа Pink Floyd собирается дать новый концертный тур по всему миру. По предыдущему опыту группа знает, что солист Роджер Уотерс постоянно нервничает при перелетах. На некоторых маршрутах он теряет вес от волнения, а на других - много ест и набирает вес.
Известно, что чем больше весит Роджер, тем лучше выступает группа, поэтому требуется спланировать перелеты так, чтобы вес Роджера на каждом концерте был максимально возможным. Группа должна посещать города в том же порядке, в котором она дает концерты. При этом между концертами группа может посещать промежуточные города.
Первая строка входного файла содержит три натуральных числа n, m и k - количество городов в мире, количество рейсов и количество концертов, которые должна дать группа соответственно (n≤100, m≤104, 2≤k≤104). Города пронумерованы числами от 1 до n. Следующие m строк содержат описание рейсов, по одному на строке. Рейс номер i описывается тремя числами bi, ei и wi - номер начального и конечного города рейса и предполагаемое изменение веса Роджера в миллиграммах (1≤bi,ei≤n, −105≤wi≤105). Последняя строка содержит числа a1, a2, ..., ak - номера городов, в которых проводятся концерты. В начале концертного тура группа находится в городе a1.Гарантируется, что группа может дать все концерты.
Первая строка выходного файла должна содержать число s - количество рейсов, которые должна сделать группа. Вторая строка должна содержать s чисел - номера используемых рейсов. Не существует такой последовательности маршрутов между концертами, что Роджер будет набирать вес неограниченно.
4 8 5 1 2 -2 2 3 3 3 4 -5 4 1 3 1 3 2 3 1 -2 3 2 -3 2 4 -10 1 3 1 2 4
6 5 6 5 7 2 3
После тысячелетнего правления большей частью Млечного Пути начался окончательный распад КОсмического ОБъединения ОЛигархов на несколько независимых монархий. КОБОЛ является высокоорганизованной империей, которая имеет форму огромного прямоугольного параллепипида n * m * k парсеков. Империя КОБОЛ сильно засекречена, поэтому лишь немногие знают точные значения n, m и k. Для облегчения контроля империя разделена на nmk маленьких владений по одному кубическому парсеку каждое. Эти владения занумерованы следующим образом:
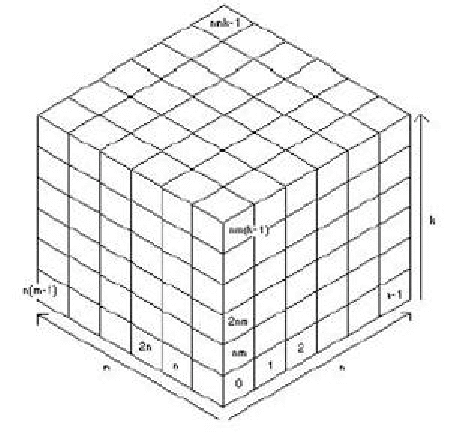
На вход может подаваться сразу несколько тестов. Первая строка содержит положительное целое число - количество тестов. Первая строка каждого отдельного теста содержит четыре целых числа: n m k l, где n, m и k (1 ≤ n, m, k ≤ 30) — размеры империи, а l — количество независимых монархий, на которое должна распасться империя. Далее следуют l строк с описаниями монархий. Каждая из них имеет следующий вид: p d1 d2 ... dp , где p — количество владений, входящих в монархию (1 ≤ p ≤ 20), а d1, ..., dp — номера этих владений. Монархии перечислены в порядке их отделения от империи.
Для каждого теста вы должны на отдельной строке выдать одно целое число — количество месяцев, в течение которых империя будет не связна.
2 2 2 3 9 2 4 5 3 6 8 10 1 7 1 2 1 11 1 9 1 1 1 0 1 3 2 2 3 3 4 0 1 2 3 4 4 5 6 7 4 8 9 10 11
4 0
В плоской стране все было как в настоящей, только плоское, и люди и горы и все, все, все. Жили в этой стране люди хорошие, но иногда попадались преступники и тогда их отвозили на плоский остров и там оставляли поразмыслить о жизни. А чтобы они не сбежали с острова, было решено построить наблюдательную вышку, с которой можно было бы следить за преступниками. Но, так как жители страны были плоскими, то и мозги у них были тоже плоскими и никак они не могли определить, в каком месте построить вышку и какой высоты. Помогите им. Вам предлагается найти самую низкую точку — координаты верхней точки вышки (плоские люди были экономными), из которой видно крайние точки острова, и найти высоту вышки. Как выяснили плоские ученые, профиль острова позволял построить вышку высотой не более 20000 метров. Профиль острова — это ломаная, имеющая примерно такой же вид как на рисунке. На острове нет лагун и с каждой вершины видны оба склона этой вершины. Точки С и Д — это крайние точки острова. 
Файл входных данных в первой строке содержит одно натуральное число N — количество вершин ломаной, не считая концов A и B. (1 ≤ N ≤ 1000) Во второй строке четыре целых числа x1, y1, x2, y2 — координаты точек A и B. ( - 1000 ≤ xi, yi ≤ 1000) В последующих N строках по два целых числа — координаты вершин xi, yi ломаной, данных в порядке обхода от А к В.( - 1000 ≤ xi, yi ≤ 1000)
Выходной файл должен содержать в первой строке два вещественных числа — координаты вершины вышки, во второй строке одно вещественное число — высоту вышки. Все числа с тремя знаками после десятичной точки. Если ответов несколько, то выведите самый левый из них.
3 0 0 100 0 20 20 40 20 70 30
50.000 50.000 26.667
Новый Мытищинский театр «Фэст» украшен гигантской гирляндой, управляемой компьютером, в которой используются тысячи лампочек. Каждый ряд лампочек в гирлянде управляется набором переключателей, которые контролируются с использованием специальной компьютерной программы. К сожалению, электрики установили неверный набор переключателей, а сегодня вечером состоится открытие театра. Ваша задача — написать программу, которая бы заставила переключатели работать корректно. Ряд лампочек в гирлянде состоит из n лампочек и контролируется n переключателями. Лампочки и переключатели занумерованы слева направо от 1 до n. Каждая лампочка может быть либо включена, либо выключена. Каждый тестовый пример в этой задаче будет содержать начальную и желаемую конечную конфигурации лампочек. Исходно предполагалось, что каждый переключатель будет контролировать одну лампочку. Однако ошибка в электронике привела к тому, что каждый переключатель помимо своей лампочки также изменяет состояние двух (или одной, если основная лампочка находится c краю) соседних с ней. Так, самый левый переключатель (i = 1) изменяет состояние двух самых левых лампочек (1 и 2), а самый правый (i = n) — двух самых правых (n - 1 и n). Каждый из оставшихся переключателей (1 ≤ i ≤ n) изменяет состояние трех лампочек с номерами i - 1, i и i + 1. Исключение составляет единственный случай, когда имеется ровно одна лампочка и один переключатель. В этом случае этот переключатель контролирует эту лампочку. Таким образом, если, к примеру, лампочка 1 включена, а лампочка 2 выключена, то при нажатии на переключатель 1 лампочка 1 выключится, а лампочка 2 включится. Определим минимальную стоимость перехода из одной конфигурации к другой как минимальное количество переключателей, которое требуется нажать, чтобы получить из начальной конфигурации конечную.
Можно представить состояние ряда лампочек как двоичное число, где 0 означает, что лампочка выключена, а 1 — что лампочка включена. Так, в частности, двоичное число 01100 представляет собой ряд из пяти лампочек, среди которых вторая и третья включены, а остальные выключены. Можно превратить эту конфигурацию в конфигурацию 10000, нажав последовательно на переключатели 1, 4 и 5, но дешевле сделать это, просто изменив состояние переключателя 2. Напишите программу, которая определит, на какие переключатели следует нажать, чтобы перевести начальную конфигурацию лампочек в конченую за минимальной стоимость. В некоторых случаях подобное может оказаться невозможным. Отметим, что для компактности представления двоичные числа записываются как десятичные, то есть вместо 01100 и 10000 используются числа 12 и 16 соответственно.
Входной файл содержит несколько тестовых примеров. Каждый тестовый пример занимает одну строку. Строка содержит два неотрицательных целых десятичных числа, по крайней мере одно из которых положительно и каждое из которых содержит не более 100 цифр. Двоичная запись первого числа представляет собой начальную конфигурацию, а второго — конечную. Чтобы избежать проблем с ведущими нулями, будем предполагать, что первая лампочка либо в начальной, либо в конченой конфигурации включена. Во входном файле не будет пробелов в начале или конце строки, числа записаны без ведущих нулей и разделены ровно одним пробелом. Последняя строка входного файла содержит два нуля.
Для каждого тестового примера выведите в выходной файл одну строку. Она должна содержать номер тестового примера и десятичное число, двоичное представление которого кодирует набор переключателей, которые требуется нажать, чтобы из начальной конфигурации получить конечную. В двоичном представлении этого числа самый правый (наименее значимый) бит должен соответствовать переключателю с номером n, 1 означает, что переключатель следует нажать, а 0 — что нет. Если решения не существует, то вместо этого числа следует вывести слово “impossible”. Если имеется более одного решения, выведите то, которое представляется меньшим десятичным числом. Разделяйте вывод для тестовых примеров пустой строкой. Используйте формат, приведенный в примере.
12 16 1 1 3 0 30 5 7038312 7427958190 4253404109 657546225 0 0
Case Number 1: 8 Case Number 2: 0 Case Number 3: 1 Case Number 4: 10 Case Number 5: 2805591535 Case Number 6: impossible