Алгоритмы(1657 задач)
Структуры данных(279 задач)
Интерактивные задачи(17 задач)
Другое(54 задач)
Мэр одного большого города решил ввести плату за проезд по шоссе, проходящим в районе города, чтобы снизить объем транзитного транспорта. В районе города проходит n шоссе.
Но руководство области, в которой расположен город, воспротивилось планам мэра. Действительно – дальнобойщики представляют собой неплохой источник доходов для большого количества кафе и гостиниц в небольших городках.
В результате решили, что плата будет введена только на шоссе, которые проходят через город.
В городе используется развитая система метрополитена, всего в городе есть m станций метро. Решено было, что шоссе проходит через город, если либо одна из станций метро расположена непосредственно на шоссе, либо есть хотя бы одна станция с каждой стороны от шоссе.
Помогите теперь мэру определить, какие шоссе проходят через город.
Первая строка входного файла содержит два целых числа: n и m – количество шоссе и количество станций метро, соответственно (1 ≤ n, m ≤ 100 000).
Следующие n строк описывают шоссе. Каждое шоссе описывается тремя целыми числами a, b и c и представляет собой прямую на плоскости, задаваемую уравнением a×x+b×y+c = 0 (|a|, |b|, |c| ≤ 106). Следующие m строк входного файла описывают станции метро. Каждая станция описывается двумя целыми числами x и y и представляет собой точку на плоскости с координатами (x, y) (|x|, |y| ≤ 106).
Первая строка выходного файла должна содержать одно целое число – количество шоссе, которые проходят через город. Вторая строка должна содержать номера этих шоссе в возрастающем порядке. Шоссе нумеруются от 1 до n в порядке, в котором они описаны во входном файле.
Система тестов состоит из двух групп:
В тестах первой группы выполняется ограничение \(n \le 10^4\). За прохождение этой группы ставится 50 баллов.
В тестах второй группы дополнительных ограничений нет. За прохождение этой группы ставится также 50 баллов.
4 2 0 1 0 1 0 1 1 1 0 1 1 -1 0 0 2 0
3 1 3 4
Задана последовательность из n чисел a1, a2, ..., an. Подпоследовательностью длины k этой последовательности называется набор индексов i1, i2, ..., ik, удовлетворяющий неравенствам 1 ≤ i1 < i2 < ... < ik ≤ n. Подпоследовательность называется возрастающей, если выполняются неравенства ai1 < ai2 < ... < aik.
Необходимо найти число возрастающих подпоследовательностей наибольшей длины заданной последовательности a1, ... ,an. Так как это число может быть достаточно большим, необходимо найти остаток от его деления на 109 + 7.
Первая строка входного файла содержит целое число n (1 ≤ n ≤ 105). Вторая строка входного файла содержит n целых чисел: a1, a2, ... ,an. Все ai не превосходят 109 по абсолютной величине.
В выходной файл выведите ответ на задачу.
5 1 2 3 4 5
1
6 1 1 2 2 3 3
8
В области Тампере существуют станции обслуживания мобильных телефонов четвертого поколения, которые работают следующим образом. Вся область разделена на квадраты. Квадраты формируют матрицу S×S, строки и столбы которой нумеруются с 0 до S - 1. Каждый квадрат содержит одну станцию обслуживания. Количество активных мобильных телефонов внутри квадрата может меняться, потому что телефон может перемещаться из одного квадрата в другой или выключаться. Временами каждая станция обслуживания передает сведения об изменении в количестве активных телефонов на главную станцию обслуживания (вместе с номером строки и столбца матрицы).
Напишите программу, которая принимает эти сведения и отвечает на запросы о текущем количестве активных мобильных телефонов в любой прямоугольной области.
Каждый запрос к программе описывается на отдельной строке и состоит из одного целого числа, описывающего команду, а также из дополнительных параметров команды в соответствии со следующей таблицой:
| Команда | Параметры | Значение |
|---|---|---|
| 0 | S | Инициализирует матрицу размером S×S, состоящую только из нулей. Эта команда поступает один раз и является самой первой командой. |
| 1 | X Y A | Добавить число A к количеству активных мобильных телефонов в квадрате (X;Y). Число A может быть как положительным, так и отрицательным. |
| 2 | L B R T | Выдать текущую сумму количеств активных мобильных телефонов во всех квадратах (X;Y), где L ≤ X ≤ R, B ≤ Y ≤ T. |
| 3 | Прервать программу. Эта команда поступает один раз и является самой последней командой. |
Все значения всегда лежат в правильном диапазоне, поэтому нет необходимости их проверять. В частности, если число A отрицательное, то число активных телефонов в каком-либо квадрате все равно не станет меньше нуля. Индексы начинаются с 0, поэтому, например, для таблицы размера 4×4 имеем 0 ≤ X ≤ 3, 0 ≤ Y ≤ 3.
Ваша программа не должна отвечать ни на какую команду, кроме 2. Если команда 2, то ваша программа должна вывести единственную строку, содержащую одно целое число — ответ на этот запрос.
| Размер таблицы | S×S | 1×1 ≤ S×S ≤ 1024×1024 |
| Значение ячейки в любой момент времени | V | 0 ≤ V ≤ 215 - 1 (= 32767) |
| Величина обновления | A | -215 ≤ A ≤ 215 - 1 (= 32767) |
| Количество команд | U | 3 ≤ U ≤ 60002 |
| Максимальное количество активных телефонов во всей таблице | M | M = 230 |
0 4 1 1 2 3 2 0 0 2 2 1 1 1 2 1 1 2 -1 2 1 1 2 3 3
3 4

Многие пользователи мобильных телефонов при наборе sms-сообщений используют режим T9. При этом сообщения, например на английском языке, они набирают следующим образом. Для набора слова по буквам соответствующая букве кнопка нажимается один раз, вне зависимости от того, сколько букв соответствуют этой кнопке, и какой по счету идет нужная буква (см. картинку), а программа в телефоне подбирает из имеющегося словаря подходящее для данной комбинации кнопок слово. Если подходящих слов несколько, то в первую очередь предлагается наиболее часто встречающееся слово (изначально слова одинаковой встречаемости предлагаются по алфавиту). Если слово не подошло, то пользователь нажимает кнопку ‘*’ и программа предлагает второе по встречаемости слово, образуемое той же комбинацией кнопок (в первую очередь следующее слово с той же частотой встречаемости, если такое имеется). Если и оно не подошло, то кнопка ‘*’ нажимается еще раз и т.д. Для простоты будем считать, что современные модели телефонов содержат полный словарь используемых слов, и нужное слово обязательно найдется. Когда предлагаемое слово подошло, пользователь нажимает на кнопку “пробел”, нажимает на кнопку ‘1’ (последняя соответствует набору знака препинания), или заканчивает набирать сообщение. Когда знак препинания не подошёл, опять же нажимается кнопка ‘*’, до тех пор пока не появится требуемый знак. После набора пробела или знака препинания пользователь может ввести ещё один пробел или знак препинания, начать набирать следующее слово или закончить набирать сообщение. Будем считать, что пользователю достаточно трех знаков препинания, и они предлагаются в следующем порядке: точка (‘.’), запятая (‘,’), вопросительный знак (‘?’). После того как пользователь “утвердил” набранное слово (нажав на пробел или ‘1’), частота его встречаемости в словаре увеличивается на 1, и новое значение частоты учитывается, в том числе, и при наборе в режиме T9 остальных слов того же сообщения. При этом данное слово будет предлагаться первым среди слов с такой же частотой встречаемости, порядок предложения остальных слов остается неизменным. Когда появится еще одно слово с той же частотой, то уже оно будет предлагаться первым, не меняя порядка остальных, и т. д. Вам требуется написать программу, которая по имеющемуся словарю, содержащему первоначальные характеристики частоты встречаемости того или иного английского слова, и известной последовательности нажатий кнопок пользователем при наборе sms-сообщения в режиме T9 воспроизведет появившееся на экране сообщение.
В первой строке входного файла находится целое число N (3 ≤ N ≤ 50000) — количество слов в словаре. В каждой из следующих N строк записаны одно слово словаря и через пробел натуральное число F (1 ≤ F ≤ 1000) — первоначальное значение частоты встречаемости этого слова (чем больше значение, тем чаще встречается данное слово). Числовая характеристика частоты встречаемости отделена от слова ровно одним пробелом. Слова в словаре состоят только из строчных английских букв и расположены в алфавитном порядке. Длина слова не превышает 20 символов. Все слова не пустые и различные. Последняя строка файла состоит из цифр от 1 до 9 и символов “пробел” и ‘*’, обозначающих последовательность нажатий кнопок при наборе сообщения. Длина этой строки не превосходит 100000 символов.
Выведите в выходной файл текст sms-сообщения.
5 ad 2 be 1 not 10 or 5 to 50 86 23* 67 668 86 231**
to be or not to be?
3 act 1 bat 1 cat 1 228* 228** 228** 228**1
bat cat act bat.
Лена играет в машинки. Для этого она вырезала из бумаги машинку (являющуюся многоугольником без самопересечений и самокасаний) и стала возить её по столу. К сожалению, во время игры она разлила чай и на столе образовалась река. Для того, чтобы продолжить игру, Лене нужно провезти машинку через реку. Для этого она решила построить мост — длинную ленту, по которой и поедет машинка. На столе машинку можно поворачивать на любой угол, но для того, чтобы проехать через реку, её границы не должны выходить за границы моста. Ниже расположена фотография игрового поля и предполагаемое решение проблемы. Лене стало интересно — какой минимальной ширины может быть мост, чтобы машинка смогла проехать через реку?
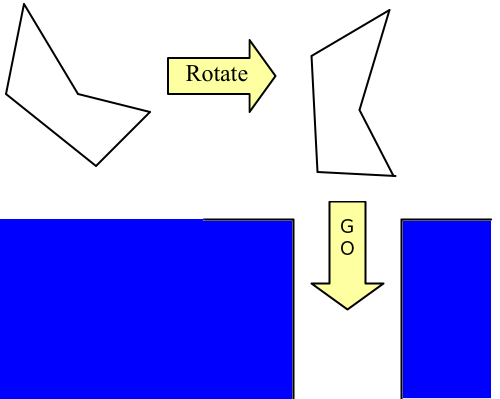
Внезапно Лена задумалась — ведь эта игра может стать прекрасной задачей по информатике, достойной финала международной студенческой олимпиады! Её Вам и предстоит решить.
Первая строка входного файла содержит T (Первая группа тестов: 0 < T < 11, вторая группа тестов: T = 1) -- количество тестов во входном файле. Далее следуют T тестов. Первая строка теста содержит число N (Первая группа тестов: 3 <= N <= 100. Вторая группа: 3 <= N <= 2 * 105) — количество вершин многоугольника.
Следующие N строк содержат по два числа — xi и yi (Первая группа тестов: 0 <= xi, yi <= 1000. Вторая группа: -105 <= xi, yi <= 105), задающие координаты многоугольника в порядке обхода. Гарантируется, что он не имеет самокасаний и самопересечений.
Для каждого теста на новой строке выведите одно число c точностью до двух знаков округляя в большую сторону — минимально требуемую ширину моста, при которой машинка сможет проехать через реку.
2 3 0 0 3 0 0 4 4 0 10 10 0 20 10 10 20
2.4000 14.1422