#111828

Швабра

Темы: [Вычислительная геометрия]

Источники: [ Командные олимпиады, ВКОШП, 2012, Задача J ]

Первокурсник Рома приехал в общежитие и, удивившись беспорядку в комнате и толстому слою пыли на полу, начал наводить порядок. Первым делом он решил вымыть пол. Для этого Рома в магазине приобрел инновационную швабру.

Изначально моющая часть швабры имела идеальную прямоугольную форму, но в процессе перевозки из магазина в общежитие у нее отломился один из углов. Таким образом, теперь она представляет собой многоугольник, граница которого состоит из двух соседних сторон прямоугольника, фрагментов двух оставшихся сторон и ломаной, соединяющей концы этих фрагментов.

$\text{[math]}$

Рома живет в большой прямоугольной комнате. Рома провел сломанной шваброй от одной стороны комнаты до другой, не отрывая ее от стены, так что в результате отломанный угол швабры оказался в углу комнаты. При этом часть соответствующей прямоугольной полосы пола в углу осталась невымытой.

$\text{[math]}$

Рома считает, что все точки, в которых в какой-то момент находилась моющая часть швабры оказались вымыты. Теперь он решил выяснить, какая часть этой полосы осталась грязной.

$\text{[math]}$

Помогите ему вычислить площадь этой части. Можете считать, что размер комнаты, в которой живет Рома, существенно больше размеров моющей части швабры.

Формат входного файла

Первая строка входного файла содержит два целых числа $w$ и $h$ - размеры моющей части швабры до повреждения ($2 \le w, h \le 10^5$).

Вторая строка содержит целое число $n$ - число вершин ломаной, соединяющей соседние стороны швабры ($2 \le n \le 10^5$). В $i$-й из следующих $n$ строк заданы два целых числа $x_i$ и $y_i$ ($1 \le x_i < w$, $1 \le y_i < h$, за исключением $y_1 = h$, $x_n = w$) - координаты $i$-й вершины ломаной. Ломаная не имеет самопересечений и самокасаний.

Координаты введены таким образом, что стена, вдоль которой Рома провел шваброй, соответствует прямой $y=h$.

Формат выходного файла

В выходной файл выведите площадь невымытой части пола с абсолютной или относительной погрешностью не более $10^{-6}$. Это значит, что если правильный ответ $a$, а вы вывели $p$, то ваш ответ будет засчитан как правильный, если $\frac{|a-p|}{\max(|a|, 1)}\le 10^{-6}$.

Примеры

Входные данные

Выходные данные

18.0

#111830

Количество вызовов функции Фибоначчи

Темы: [Рекурсия]

Как известно, очередное число Фибоначчи равно сумме предыдущих двух. Первое и второе число Фибоначчи равны единице.

Программист Вася написал вычисление n-ого числа Фибоначчи с помощью рекурсивной функции. А сколько раз запустится эта функция прежде, чем будет получено значение?

Входные данные

Дано одно число n ( 1 ≤ n ≤ 50 )

Выходные данные

Выведите одно число — количество запусков функции.

Примеры

Входные данные

Выходные данные

Входные данные

Выходные данные

Входные данные

Выходные данные

#111838

Буква и цифра

Темы: [Строки]

Даны два символа, каждый в своей строке. Если это латинская буква (строчная или заглавная) и цифра (неважно, в каком порядке), выведите YES, иначе NO.

Входные данные

Даны два символа, каждый в своей строке.

Выходные данные

Если это латинская буква (строчная или заглавная) и цифра (неважно, в каком порядке), выведите YES, иначе NO.

Примеры

Входные данные

1
a

Выходные данные

YES

Входные данные

1
2

Выходные данные

NO

#111846

Карта метро

Темы: [Обход в глубину]

Источники: [ Командные олимпиады, Московская командная олимпиада, 9-11 классы, 2013, Лига А, Задача E ]

В одном уездном городе Эн было решено построить собственное метро. Все силы города были мобилизованы на выкапывание станций и прокладку подземных путей дедовскими лопатами.

Вся эта история нас бы совершенно не интересовала, если бы однажды в мэрию города не пришло письмо из далёкой страны Емакира. Оказалось, что компания Alpep подозревает администрацию уездного города в нарушении их патента на jMetro и грозится возбудить против города Эн дело. Согласно патенту, jMetro — это метро, в котором:

существует ровно одна узловая станция, в которой начинаются все радиальные линии метро, и это единственная станция, принадлежащая хотя бы двум радиальным линиям;
существует ровно одна кольцевая линия, все станции которой лежат на радиальных линиях, причём на каждой радиальной линии лежит ровно одна станция кольцевой линии;
кольцевая линия не проходит через узловую станцию;
кольцевая линия не проходит через конечные станции радиальных линий.

$\text{[math]}$

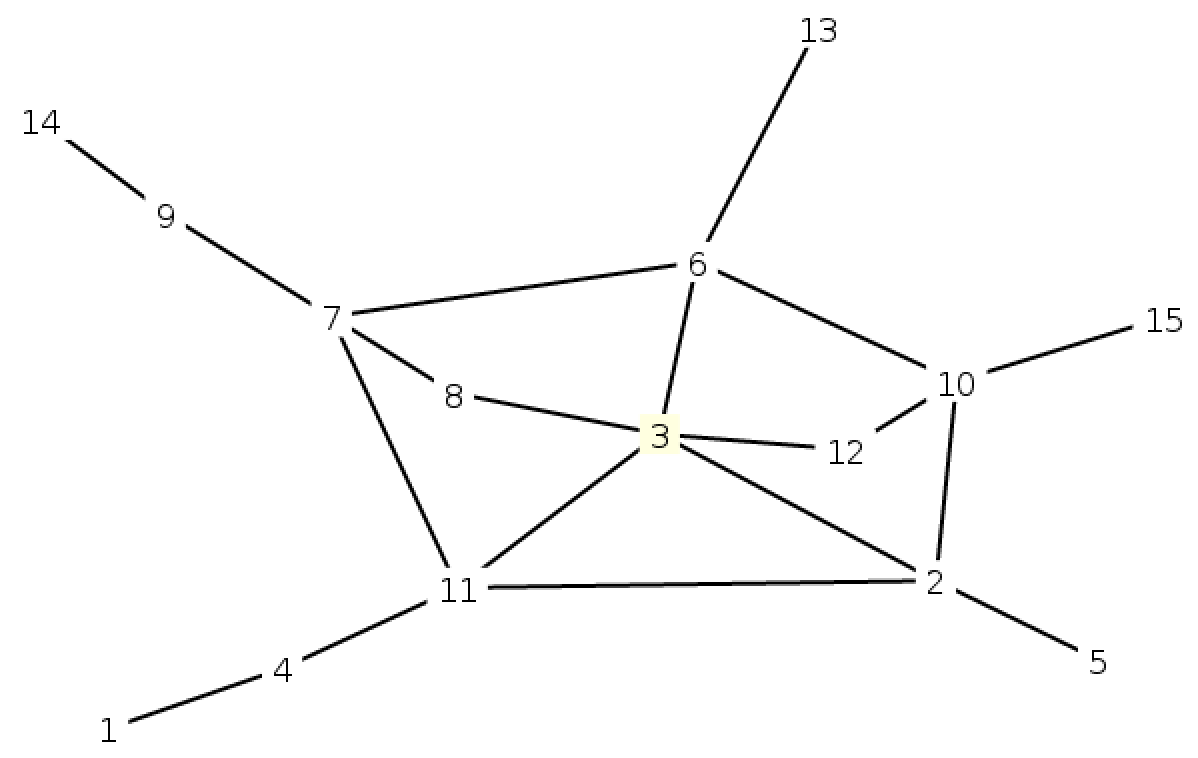
Поскольку компания Alpep известна своими необоснованными обвинениями в нарушениях патентов, мэрия города хочет проверить правомочность заявления компании.

Входные данные

В первой строке заданы два числа N и M ( 1 ≤ N , M ≤ 2·10 ⁵ ) — количество станций метро и перегонов между ними. Следующие M строк содержат описания перегонов: каждая из них содержит по два числа — номера станций, между которыми есть перегон. По каждому перегону составы могут ездить как в одну, так и в другую сторону. Между любыми двумя станциями существует не более одного перегона. Никакой перегон не соединяет станцию саму с собой.

Выходные данные

Выведите « YES », если метро уездного города Эн нарушает патент jMetro, и « NO » в противном случае.

Примечание

Первый пример соответствует рисунку из условия.

Примеры

Входные данные

Выходные данные

YES

Входные данные

Выходные данные

NO

#111854

Пирожные

Темы: [Условный оператор (if)]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Муниципальный этап, Москва, 2012, Задача A ]

Для праздничного чаепития необходимо купить $n$ пирожных. В магазине продается всего два вида пирожных, причем пирожных одного вида осталось $a$ штук, а пирожных другого вида осталось $b$ штук. Пирожные одного вида считаются одинаковыми. Сколькими способами можно купить ровно $n$ пирожных?

Входные данные

В первой строке входных данных записано число $n$ — количество пирожных, которое нужно купить, во второй и третьей строке записаны числа $a$ и $b$ — количество пирожных каждого из двух видов, которые есть в магазине. Все числа — целые, от 1 до 100.

Выходные данные

Программа должна вывести одно целое число — количество различных способов купить $n$ пирожных.

Примечание

В примере из условия купить 5 пирожных можно 4 способами: 0 пирожных первого вида и 5 пирожных второго вида, 1 пирожное первого вида и 4 пирожных второго вида, 2 пирожных первого вида и 3 пирожных второго вида, 3 пирожных первого вида и 2 пирожное второго вида. Больше способов нет, так как в магазине есть только 3 пирожных первого вида.

Примеры

Входные данные

5
3
10

Выходные данные