Алгоритмы(1657 задач)
Структуры данных(279 задач)
Интерактивные задачи(17 задач)
Другое(54 задач)
Черный ящик организован наподобие примитивной базы данных. Он может хранить набор целых чисел и имеет выделенную переменную i . В начальный момент времени черный ящик пуст, а значение переменной i =0. Черный ящик обрабатывает последовательность поступающих команд (запросов). Существуют два типа запросов:
Рассмотрим возможную последовательность из 11 запросов:
|
№ |
Запрос
|
i |
Содержимое черного ящика после запроса (элементы расположены в порядке неубывания) |
Ответ |
|
1 |
ADD (3) |
0 |
3 |
|
|
2 |
GET |
1 |
3 |
3 |
|
3 |
ADD (1) |
1 |
1, 3 |
|
|
4 |
GET |
2 |
1, 3 |
3 |
|
5 |
ADD (-4) |
2 |
-4, 1, 3 |
|
|
6 |
ADD (2) |
2 |
-4, 1, 2, 3 |
|
|
7 |
ADD (8) |
2 |
-4, 1, 2, 3, 8 |
|
|
8 |
ADD (-1000) |
2 |
-1000, -4, 1, 2, 3, 8 |
|
|
9 |
GET |
3 |
-1000, -4, 1, 2, 3, 8 |
1 |
|
10 |
GET |
4 |
-1000, -4, 1, 2, 3, 8 |
2 |
|
11 |
ADD (2) |
4 |
-1000, -4, 1, 2, 2, 3, 8 |
|
Требуется разработать эффективный алгоритм, обрабатывающий заданную последовательность запросов. Максимальное допустимое количество запросов ADD и GET — по 30000 каждого типа. Последовательность запросов будем задавать двумя наборами чисел:
Файл исходных данных содержит (в указанном порядке): M , N , A (1), A (2), ..., A ( M ), u (1), u (2), ..., u ( N ) . Все числа разделяются пробелами и (или) символами перевода строки.
Вывести в выходной файл последовательность ответов черного ящика для заданной последовательности запросов. Числа в выходном файле могут разделяться пробелами и символами перевода строки.
7 4 3 1 -4 2 8 -1000 2 1 2 6 6
3 3 1 2
Как известно, Нью-Йорк большой город. На главной улице находится N небоскребов в ряд, в i - м небоскребе есть A i свободных офисов. Недавно в городе образовались M компаний. Каждой из них конечно нужны офисы, но управляющие i - й компании хотят получить по офису в каждом небоскребе с L i по R i . Напишите программу, которая вычислит, какое максимальное количество компаний может получить офисы на главной улице Нью-Йорка в соответствии с их требованиями.
В первой строке входных данных записаны 2 числа N и M (1 ≤ N , M ≤ 100000) . В следующих N строках записано по одному числу A i (1 ≤ A i ≤ 100000) . В следующих М строках записаны пары чисел L i и R i (1 ≤ L i ≤ R i ≤ N ) .
Выведите одно число — максимальное количество компаний, которые могут получить офисы на главной улице Нью-Йорка.
5 4 1 3 2 1 3 1 3 2 5 2 3 4 5
3
Фирма NNN решила транслировать свой рекламный ролик в супермаркете XXX. Однако денег, запланированных на рекламную кампанию, хватило лишь на две трансляции ролика в течение одного рабочего дня. И при этом обязательно транслировать ровно два рекламных ролика в день.
Фирма собрала информацию о количестве покупателей в каждый момент некоторого дня. Менеджер по рекламе предположил, что и на следующий день покупатели будут приходить и уходить ровно в те же моменты времени.
Помогите ему определить моменты времени, когда нужно включить трансляцию рекламных роликов, чтобы как можно большее количество покупателей прослушало ролик.
Ролик длится ровно одну единицу времени. Для каждого момента времени известно количество покупателей, находящихся в магазине в этот момент. Между концом первой рекламы и началом следующей должна пройти как минимум К - 1 единица времени.
Первая строка содержит два числа N (моментов времени) и K (время совершения покупки одним покупателем). Гарантируется, что N > K. ( N, K ≤ 200 000 ). Во второй строке содержится N чисел a i — количество покупателей в момент времени i . ( 0 ≤ a i ≤ 2 000 000 000 ).
Выведите единственное число — количество просмотревших рекламу покупателей.
5 2 3 5 1 4 2
9
Скоро начнётся сезон роста бамбука. Скупщики бамбука принимают любое количество бамбука каждый день ровно в полдень. Однако цена бамбука каждый день меняется. Нам удалось узнать, по какой цене скупщики будут принимать бамбук. Кроме того, мы точно знаем, на сколько метров вырастает бамбук за каждые сутки (эта величина тоже меняется). В любой день можно либо срезать весь бамбук целиком и продать его, либо оставить бамбук расти дальше. После срезания бамбук продолжает расти. Требуется определить, какую максимальную прибыль от продажи бамбука можно получить. В полдень нулевого дня (начало сезона роста бамбука) длина бамбука равна 0. Сезон роста бамбука длится ровно N суток.
В первой строке входного файла находится натуральное число N , 1 ≤ N ≤ 100000 . В каждой из следующих N строк содержатся два целых положительных числа, разделенных пробелом: цена одного метра бамбука в определенный день и на сколько метров вырос бамбук за последние сутки. В ( i + 1) - й строке файла содержатся данные, относящиеся к полудню i – го дня.
В единственной строке выходного файла следует выводить одно целое неотрицательное число – наибольшая возможная выручка от продажи бамбука. Гарантируется, что результат не превосходит 2 63 - 1 .
8 2 7 4 1 3 3 5 5 2 4 5 2 4 7 1 1
139
Поблизости от столицы Флатландии одна компания решила построить коттеджный поселок. Строительная компания, которая занимается возведением коттеджей, решила раскрасить некоторые коттеджи в розовый цвет, а остальные - в голубой. Но они не могут решить какой коттедж раскрасить в какой цвет.
Директор компании утверждает, что раскраска симпатичная, если есть хотя бы один розовый коттедж, хотя бы один голубой коттедж, и можно провести такую прямую, что все розовые коттеджи окажутся с одной стороны от нее, я голубые - с другой стороны (при этом на самой прямой коттеджей быть не должно). На это главный дизайнер возразил, что есть несколько способов сделать симпатичную раскраску.
Помогите им определить, сколько существует различных симпатичных раскрасок.
Первая строка входного файла input.txt содержит число n - количество коттеджей (1 ≤ n ≤ 300) . Следующие n строк содержат координаты коттеджей, каждая строка содержит два целых числа x i и y i ( - 10 4 ≤ x i , y i ≤ 10 4 ) .
Выведите в файл output.txt одно число - количество симпатичных раскрасок коттеджного поселка.
Возможные раскраски приведены на следующем рисунке.
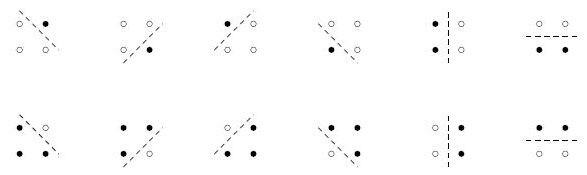
4 0 0 1 0 1 1 0 1
12