Темы --> Информатика
    Язык программирования(952 задач)
    Алгоритмы(1657 задач)
    Структуры данных(279 задач)
    Интерактивные задачи(17 задач)
    Другое(54 задач)
---> 2656 задач <---
Источники
    Личные олимпиады(938 задач)
    Командные олимпиады(684 задач)
Страница: << 476 477 478 479 480 481 482 >> Отображать по:
#112543
Дана строка...
  
Темы: [Строки]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Назовем качеством строки разность между максимальным и минимальным номерами в алфавите букв, входящих в строку. Например, качество строки ab равно 2 – 1 = 1 , а строки abcz равно 26 – 1 = 25 .

Дана строка s . Необходимо найти непустую подстроку этой строки, обладающую максимальным качеством, а из всех таких — минимальную по длине.

Входные данные

Входной файл содержит непустую строку s , состоящую из строчных букв латинского алфавита. Ее длина не превосходит 2 * 10 5 символов.

Выходные данные

В выходной файл выведите искомую подстроку. Если вариантов ответа несколько, выведите любой.

Примеры
Входные данные
aba
Выходные данные
ab
Входные данные
zzz
Выходные данные
z
#112544
Игра на бирже
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes

Петя пишет программы для бирж. Он занимается разработкой различных финансовых инструментов, его последний проект связан с анализом возможности арбитража с использованием исторических данных о котировках существенно волатильной акции.

Идея анализа состоит в следующем: по заданным котировкам акции в течение n последовательных дней, требуется выбрать подпоследовательность котировок, которая удовлетворяет следующему свойству: любые две соседние котировки в выбранной подпоследовательности должны отличаться не менее чем на k . Например, если котировки равны, соответственно, 1014, 1024, 1034, 1045, 1030, 998 и k = 15 , то подпоследовательность котировок 1014, 1034, 998 является допустимой. Выбранная подпоследовательность должны быть как можно длиннее. Так, в приведенном примере выбранная последовательность не является оптимальной, подпоследовательность 1014, 1045, 1030, 998 лучше.

По заданной последовательности котировок, найдите ее длиннейшую допустимую подпоследовательность.

Входные данные

Первая строка входного файла содержит число n ( 1 ≤ n ≤ 100000 ) количество котировок и k ( 1 ≤ k ≤ 10 9 ). Вторая строка содержит n целых чисел последовательность котировок (все котировки находятся в интервале от 1 до 10 9 включительно).

Выходные данные

Первая строка выходного файла должна содержать l — длину оптимальной подпоследовательности. Вторая строка должна содержать l целых чисел элементы любой такой подпоследовательности.

Примеры
Входные данные
6 15
1014 1024 1034 1045 1030 998
Выходные данные
4
1014 1045 1030 998
#112545
Шоу
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Главный режиссер шоу, посвященного открытию ACM Programming Contest, хочет, чтобы участники шоу могли выстраиваться в различное число колонн ровно N способами. Причем при любом перестроении количество людей в каждой из колонн должно быть одинаковым. Требуется сообщить режиссеру, какое минимальное число М человек ему для этого понадобится. Так, при N = 3 потребуется пригласить всего М = 4 человек, которые могут выстроиться в 1, 2 и 4 колонны. Если же при некотором N для шоу потребуется более 10 9 человек, то режиссеру можно сообщить, что подходящее число людей собрать невозможно.

Входные данные

Программа запрашивает натуральное число N ≤ 1000

Выходные данные

Если для введенного N минимальное число людей М для шоу не превосходит 10 9 , то выдать это число М , в противном случае число 0.

Примеры
Входные данные
5
Выходные данные
16
Входные данные
6
Выходные данные
12
Входные данные
24
Выходные данные
360
#112546
Кубок Гагарина
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes

Хоккей с шайбой  — один из самых распространенных в России видов спорта. На днях закончился розыгрыш самого престижного в Европе хоккейного клубного турнира  — Кубка Гагарина.

На первом этапе плей-офф борьбу начинает 16 клубов, разбитые по парам. Далее команды, попавшие в одну пару играют между собой серию из семи матчей до четырех побед. Если одна из команд выигрывает четыре матча, то серия прекращается и она признается победителем. Далее остается восемь команд, которые играют второй раунд по тем же правилам, и так далее, вплоть до победителя.

Первые два матча серии проходят на площадке первой команды, следующие два на площадке второй команды, после этого следующие матчи (если они нужны) проходят поочередно сначала на площадке первой команды, потом второй, то есть по схеме 2-2-1-1-1.

Вам дана вероятность победы каждой из команд на каждой из площадок. Вам нужно определить вероятность, с которой серия завершится именно с данным счетом.

Входные данные

Первая строка входного файла содержит вещественных два числа a и b — вероятность победы каждой из команд на площадке первой команды ( 0 ≤ a , b ≤ 1, a + b = 1 ), вторая строка в аналогичном формате вероятность побед из команд на площадке второй команды. Третья строка содержит счет, вероятность которого Вам нужно определить.

Выходные данные

Выведите одно число  — ответ на задачу. Ответ должен отличаться от правильного не более, чем на 10 - 6 .

Примеры
Входные данные
0.7 0.3
0.54 0.46
4-0
Выходные данные
0.142884
#112547
НЛО2
  
Темы: [Список]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes

Служба безопасности Земли хочет уничтожить корабль враждебно настроенных инопланетян. Служба безопасности уже повредила корабль и заставила его сесть в пустыне. Корабль построен из кубических отсеков единичного размера и нижний слой имеет форму прямоугольника размером N × M . На рисунке показан пример вида сверху на корабль размером N = 4 , M = 8 .

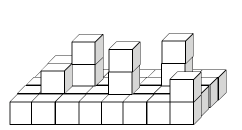
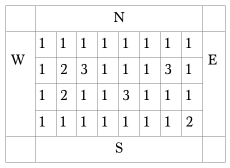
Отсеки корабля сделаны из сверхпрочного металла, поэтому для разрушения корабля используются лазеры. Лазерные установки были развернуты напротив четырех боковых сторон корабля, и они периодически выпускают лучи, перпендикулярные сторонам корабля, в сторону различных отсеков корабля. Каждый луч разрушает R первых отсеков, встретившихся на его пути. Если над уничтоженным отсеком находятся другие отсеки, то они сдвигаются вниз. Так же лазеры могут стрелять только по нижним бокам.

После K выстрелов было решено нанести по кораблю авиаудар. Для удара имеет смысл выбрать такой участок размером P × P , который целиком содержит максимальное количество уцелевших отсеков, чтобы уничтожить их все.

Напишите программу, которая вычислит, какое количество целых блоков сможет уничтожить авиаудар, нанесенный на участке размером P × P .

Входные данные

В первой строке входного файла даны 5 целых чисел: N , M ( 1 ≤ N · M ≤ 1 000 000 ), R ( 0 < R ≤ 10 ), K ( 0 < K ≤ 300 000 ) и P ( 0 < P ≤ min ( N , M , 10) ). В каждой из следующих N строк записаны по M чисел. Число в i -ой строке и j -ом столбце описывает количество единичных блоков в соответствующей части корабля аналогично рисунку. Каждое число находится в диапазоне 1..10 6 .

В следующих K строках описаны выстрелы из лазеров. Каждая из этих строк содержит один символ и через пробел от него число. Символы определяют сторону воздействия: "W" — запад, "E" — восток, "S" — юг, "N" — север. Число определяет номер строки в случае запада и востока или столбца в случае севера и юга. Строки и столбцы соответствуют нумерации из входных данных, слои нумеруются с единицы. Каждое число находится в диапазоне 1..10 6 .

Выходные данные

Выведите максимальное количество уцелевших отсеков после K выстрелов лазерами на участке размером P × P .

Примечание
Примеры
Входные данные
4 8 2 6 2
1 1 1 1 1 1 1 1
1 2 3 1 1 1 3 1
1 2 1 1 3 1 1 1
1 1 1 1 1 1 1 2
N 2
W 2
W 2
E 2
S 4
S 7
Выходные данные
6
Страница: << 476 477 478 479 480 481 482 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест