Темы --> Информатика
    Язык программирования(952 задач)
    Алгоритмы(1657 задач)
    Структуры данных(279 задач)
    Интерактивные задачи(17 задач)
    Другое(54 задач)
---> 2656 задач <---
Источники
    Личные олимпиады(938 задач)
    Командные олимпиады(684 задач)
Страница: << 481 482 483 484 485 486 487 >> Отображать по:
#112581
Футбол
  
ограничение по времени на тест
3.0 second;
ограничение по памяти на тест
256 megabytes

N = 2 K команд играют в турнире по футболу с выбыванием.

В первом раунде играют первая команда со второй, третья с четвёртой, и так далее до последней с предпоследней.

Во втором раунде играют победитель первого матча первого раунда с победителем второго матча второго раунда, победитель третьего матча с победителем четвёртого и так далее до предпоследнего победителя первого матча с победителем последнего матча.

Аналогично играются третий, четвёртый и все раунды до K -ого.

Вам даны вероятности исходов всех возможных встреч в турнире. Определите для каждой команды вероятность того, что она выйдет из турнира - победителем.

Входные данные

Каждый тест состоит из нескольких наборов входных данных (в каждой тесте - не более пяти наборов). Число наборов указано в первой строке входного файла. Каждый набор начинается с числа команд N ( 2 ≤ N ≤ 1024, N - степень двойки). Потом идёт N строк длиной не более 10 - названия команд. Потом идёт матрица NxN , состоящая из целых чисел от 1 до 99 - j -ое число в i -ой строке это вероятность в процентах того, что i -ая команда выиграет j -ую. Вероятности будут дополненные ведущими нулями до двузначных чисел.

Выходные данные

Примеры
Входные данные
2
16
Brazil
Chile
Nigeria
Denmark
Holland
Yugoslavia
Argentina
England
Italy
Norway
France
Paraguay
Germany
Mexico
Romania
Croatia
50 65 50 60 55 50 50 65 45 55 40 55 40 55 50 50
35 50 35 45 40 35 35 50 30 40 25 40 25 40 35 35
50 65 50 60 55 50 50 65 45 55 40 55 40 55 50 50
40 55 40 50 45 40 40 55 35 45 30 45 30 45 40 40
45 60 45 55 50 45 45 60 40 50 35 50 35 50 45 45
50 65 50 60 55 50 50 65 45 55 40 55 40 55 50 50
50 65 50 60 55 50 50 65 45 55 40 55 40 55 50 50
35 50 35 45 40 35 35 50 30 40 25 40 25 40 35 35
55 70 55 65 60 55 55 70 50 60 45 60 45 60 55 55
45 60 45 55 50 45 45 60 40 50 35 50 35 50 45 45
60 75 60 70 65 60 60 75 55 65 50 65 50 65 60 60
45 60 45 55 50 45 45 60 40 50 35 50 35 50 45 45
60 75 60 70 65 60 60 75 55 65 50 65 50 65 60 60
45 60 45 55 50 45 45 60 40 50 35 50 35 50 45 45
50 65 50 60 55 50 50 65 45 55 40 55 40 55 50 50
50 65 50 60 55 50 50 65 45 55 40 55 40 55 50 50
4
Spartak
Lokomotiv
TCSKA
Anzhi
50 42 30 20
58 50 30 10
70 70 50 05
80 90 95 50
Выходные данные
Test 1:
Brazil     8.54%
Chile      1.60%
Nigeria    8.06%
Denmark    2.79%
Holland    4.51%
Yugoslavia 7.50%
Argentina  8.38%
England    1.56%
Italy      9.05%
Norway     3.23%
France     13.72%
Paraguay   3.09%
Germany    13.79%
Mexico     3.11%
Romania    5.53%
Croatia    5.53%
Test 2:
Spartak   8.61%
Lokomotiv 6.38%
TCSKA     3.50%
Anzhi     81.51%
#112589
Министерство
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Однажды в далекой-далекой стране правительство создало Министерство по сокращению бумажной волокиты. Как вы наверное догадались, это было крупнейшее министерство за всю историю страны. Количество сотрудников было поистине огромным. Несмотря на это, структура министерства была очень простой: каждый сотрудник имел не более трёх подчинённых, каждый из которых снова имел не более трех подчиненных и так далее...

В результате последних выборов был избран новый министр. Он был молод, умён и непорочен, и сразу же решил оправдать название своего учреждения. Он заметил, что многие части иерархической структуры совпадают, и решил, что должны совпадать и их обязанности. А если две структуры делают одно и тоже, одна из них является лишней, и ее работники должны быть уволены. Ваша задача найти количество различных департаментов и вывести результат в необходимом формате.

Вам дана структура министерства. Каждый работник имеет одного начальника и не более трёх подчинённых(возможно ноль). Единственным исключением является министр  — у него нет начальника(но так же не более трех подчинённых). Конечно нет определённого порядка, в котором перечисляются подчинённые. Департамент состоит из должностного лица, всех его подчинённых и их подчинённых, и т.д.

Есть два особых случая:

  • Департамент, в котором должностное лицо  — сам министр, тогда этот департамент есть всё министерство.

  • Департамент, в котором у должностного лица нет ни одного подчинённого.

Высотой департамента назовем длину максимальной последовательность сотрудников x 1 , ..., x d такую, что сотрудник x i является начальником сотрудника x i + 1 для всех 1 ≤ i < d . Заметим что высота департамента, состоящего из одного сотрудника равна 1 .

Два департамента A и B совпадают, если существует взаимно-однозначное отображение, сопоставляющее каждому сотруднику x A из департамента A сотрудника x B из департамента B , таким образом, что сотрудник x A является начальником сотрудником y A , тогда и только тогда, когда x B является начальником y B . Заметим, что если два департамента совпадают, то они имеют одинаковую высоту, одинаковое количество сотрудников и начальнику первого департамента соответствует начальник второго.

На приведенных картинках департаменты A и B совпадают, а C не совпадает ни с A , ни c B .

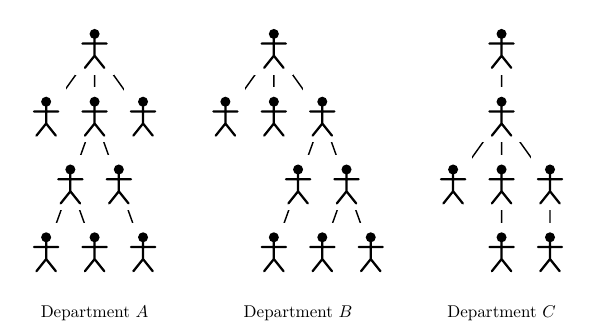
Вам необходимо для каждой высоты вычислить количество различных департаментов имеющих такую глубину. Формально требуется построить последовательность n 1 , ..., n d , где d это высота всего министерства, а n i — количество различных департаментов высоты i .

Входные данные

Входной файл содержит единственную строку, которая описывает иерархическую структуру министерства, используя следующую нотацию. Каждый департамент кодируются строкой "( x 1 ... x k )", где k — количество подчинённых у начальника департамента, а строки x i — коды им подчиняющихся департаментов. Департамент, состоящий из одного человека, кодируется строкой "()". Структура министерства задается кодом всего министерства. Количество сотрудников министерства не превосходит 1 000 000 (включая министра).

Выходные данные

Выходной файл должен содержать d строк, где d это высота министерства. i -ая строка должна содержать количество различных департаментов высоты i .

Примечание

Приведенная картинка иллюстрирует пример из условия.

Примеры
Входные данные
(((())())((()())(()()()))(()(())))
Выходные данные
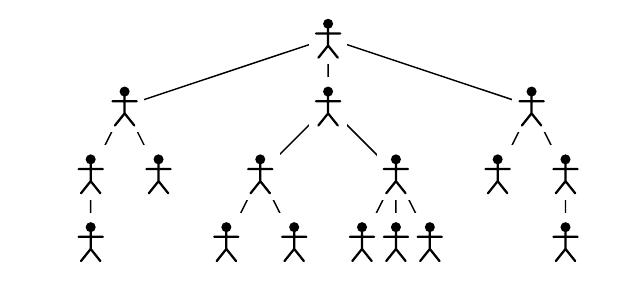
1
3
2
1
#112597
Совершенно секретно (HARD)
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

В секретном 240 отделе ИПФ РАН \(N\) сотрудников и \(N\) компьютеров. В отделе вводятся новые требования к секретности. В соответствии с этими требованиями, для каждого сотрудника будут определены ровно \(K\) компьютеров, к которым этот сотрудник будет иметь допуск (т.е. за которыми этот сотрудник будет иметь право работать), причём так, что к каждому компьютеру будут иметь допуск ровно \(K\) сотрудников.

Информация о том, какой сотрудник к какому компьютеру будет иметь допуск, будет известна лишь непосредственно перед вступлением новых требований в силу. Таким образом, чтобы не прерывать работу отдела, сотрудники должны будут быстро решить, кто за каким компьютером будет работать. Для этого им необходимо заранее написать программу, которая по любому распределению допусков сотрудников найдёт рассадку сотрудников по компьютерам, удовлетворяющую этим допускам.

Обратите внимание, что значение \(K\) тоже будет известно лишь в последний момент. Из общих соображений секретности известно лишь, что \(K\) будет равняться или 1, или 2, или 4; поэтому ваша программа должна уметь работать для любого из этих трех значений \(K\).

Формат входных данных

В первой строке входного файла записаны натуральные числа \(N\) и \(K\) (\(1\leq N \leq 100 000\)). Далее следуют \(KN\) строк, в каждой из которых записаны два натуральных числа — номер сотрудника и номер компьютера, к которому этот сотрудник имеет допуск.

Гарантируется, что каждый сотрудник имеет допуск ровно к \(K\) компьютерам, что к каждому компьютеру ровно \(K\) сотрудников имеют допуск, и что \(K\) равно либо 1, либо 2, либо 4.

Формат выходных данных

В выходной файл выведите \(N\) строк, в каждой по два числа — номер сотрудника и номер компьютера, за которым он должен работать. Строки можно выводить в произвольном порядке.

Если есть несколько решений, выведите любое. Можно доказать, что для любого входного файла, удовлетворяющего указанным ограничениям, всегда имеется как минимум одно решение.

Примеры

Ввод Вывод 
3 1
2 3
3 1
1 2

3 1
1 2
2 3

2 2
1 2
2 1
2 2
1 1

1 2
2 1
#112598
Два пути
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Как вы знаете, Васин брат живет во Флатландии. Во Флатландии n городов, соединенных n - 1 двухсторонней дорогой. Города пронумерованы от 1 до n . Из любого города можно добраться до любого другого.

Компания «Два пути», в которой работает Васин брат, выиграла тендер на ремонт двух путей во Флатландии. Путем называется последовательность различных городов, последовательно соединенных дорогами. Пути, которые надо отремонтировать, компания может выбрать самостоятельно. Единственное условие, накладываемое тендером, они не должны пересекаться (то есть иметь общих городов).

Известно, что прибыль, которую получит компания «Два пути», равна произведению длин выбранных двух путей. Считая длину каждой дороги один, а длину пути равной количеству дорог в ней, найдите максимальную возможную прибыль.

Входные данные

В первой строке записано целое число n (2 ≤ n ≤ 100 000) , где n количество городов в стране. Далее в n - 1 строке записаны сами дороги. Каждая строка содержит пару номеров соединяемых дорогами a i , b i (1 ≤ a i , b i ≤ n )

Выходные данные

Выведите максимально возможную прибыль.

Примеры
Входные данные
4
1 2
2 3
3 4
Выходные данные
1
Входные данные
7
1 2
1 3
1 4
1 5
1 6
1 7
Выходные данные
0
Входные данные
6
1 2
2 3
2 4
5 4
6 4
Выходные данные
4
#112599
Перекраска клеток
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Дано клетчатое поле N x M, все клетки поля изначально белые. Автомат умеет:

  1. Закрасить клетку (i,j) в черный цвет.
  2. Для клетки (i,j) узнать её ближайших белых соседей по вертикали и горизонтали.

Дана последовательность команд для автомата. Требуется выполнить эти команды в указанной последовательности, и для каждой команды запроса ближайших белых соседей указать результат ее выполнения.

Входные данные

начала вводятся размеры поля N и M ( 1 ≤ N ≤ 20 , 1 ≤ M ≤ 50000 ), затем количество команд K ( 1 ≤ K ≤ 10 5 ), а затем сами команды. Команды записаны по одной в строке в следующем формате:

  • Color i j — окраска клетки ( i , j ) в черный цвет;
  • Neighbors i j — нахождение белых соседей для клетки ( i , j ). (Клекта ( i , j ) может быть как белой так и черной.)

Выходные данные

На каждый запрос Neighbors требуется вывести сначала количество ближайших белых соседей (или 0 , если ни с одной из сторон белых клеток не осталось), а затем их координаты (соседей можно перечислять в произвольном порядке). Если запросов Neighbors нет, ничего выводить не надо.

Примеры
Входные данные
5 5 10
Neighbors 3 1
Color 4 1
Color 2 4
Color 4 5
Color 2 2
Neighbors 5 4
Neighbors 5 5
Neighbors 2 4
Color 3 5
Neighbors 3 5
Выходные данные
3
2 1
4 1
3 2
3
4 4
5 3
5 5
2
3 5
5 4
4
1 4
3 4
2 3
2 5
3
2 5
5 5
3 4
Страница: << 481 482 483 484 485 486 487 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест