Алгоритмы(1657 задач)
Структуры данных(279 задач)
Интерактивные задачи(17 задач)
Другое(54 задач)
Алканы (также насыщенные углеводороды, парафины, алифатические соединения) — ациклические углеводороды линейного или разветвленного строения, содержащие только простые связи. Алканы являются насыщенными углеводородами и содержат максимально возможное число атомов водорода. Каждый атом углерода в молекулах алканов находится в состоянии sp3-гибридизации — все четыре гибридные орбитали атома С идентичны по форме и энергии, четыре связи направлены в вершины тетраэдра под углами  . Cвязи C–C представляют собой σ-связи, отличающиеся низкой полярностью и поляризуемостью.
. Cвязи C–C представляют собой σ-связи, отличающиеся низкой полярностью и поляризуемостью.
Ничего не поняв, вы обратились к однокласснику за помощью. Он сказал вам забыть всё, что было написано в учебнике, и объяснил, что алканы — углеводороды. То есть соединения, состоящие из атомов углерода и водорода, не содержащие связей водород–водород, причём каждый углерод соединен ровно с четырьмя другими атомами, а каждый водород соединен ровно с одним другим атомом. При этом алкан является связным соединением, а также молекула алкана не является цикличной (для каждых двух атомов существует единственный способ добраться из одного в другой по связям между атомами). Также он сказал, что связи между атомами всегда соединяют два различных атома.
Запомнив всё это, вы пошли к Александру Евгеньевичу, и он дал вам задание: для данного соединения определить, является ли оно алканом.
В первой строке содержатся два числа N и M (1 ≤ N ≤ 100 000, 0 ≤ M ≤ 100 000) — количество атомов и соединений между атомами соответственно.
Следующая строка состоит из N символов. Если i-й символ — «C», то i-й атом — атом углерода. Если i-й символ — «H», то i-й атом — атом водорода. Гарантируется, что каждой символ этой строки — либо «C», либо «H».
В следующих M строках содержатся описания соединений между атомами. В i-й из них содержатся номера двух атомов, связанных i-м соединением.
Выведите «YES», если соединение является алканом, и «NO», если не является.
8 7
HHHCCHHH
1 4
2 4
3 4
4 5
5 6
5 7
5 8
YES
2 1
CH
1 2
NO
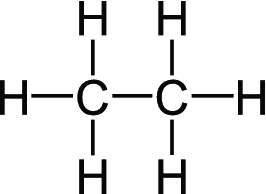
Соединение в первом примере является молекулой этана. Ниже представлена его структурная формула.
Обычно в условии задач вам долго и нудно рассказывают, что нужно сделать. Но нам это показалось скучным. В этой задаче мы сделаем по-другому. Мы скажем вам, что не нужно делать:
Дана последовательность различных целых чисел. Переставьте её как вам угодно. Единственное требование: получившаяся последовательность не должна быть отсортирована — ни по возрастанию, ни по убыванию.
В первой строке содержится единственное число T (T ≤ 1 000) — количество тестов. Каждый тест состоит из двух строк:
В первой строке содержится единственное число N (3 ≤ N ≤ 1 000) — длина последовательности чисел.
В следующей строке содержатся N различных целых чисел — элементы последовательности. Гарантируется, что каждое число не меньше - 231 и не превосходит 231 - 1.
Для каждого теста в отдельной строке выведите новую последовательность.
2
5
1 2 3 4 5
8
3 1 4 47 5 9 2 6
5 1 4 3 2
3 1 4 47 5 9 2 6
Гоблины Мглистых гор очень любях ходить к своим шаманам. Так как гоблинов много, к шаманам часто образуются очень длинные очереди. А поскольку много гоблинов в одном месте быстро образуют шумную толку, которая мешает шаманам проводить сложные медицинские манипуляции, последние решили установить некоторые правила касательно порядка в очереди.
Обычные гоблины при посещении шаманов должны вставать в конец очереди. Привилегированные же гоблины, знающие особый пароль, встают ровно в ее середину, причем при нечетной длине очереди они встают сразу за центром.
Так как гоблины также широко известны своим непочтительным отношением ко всяческим правилам и законам, шаманы попросили вас написать программу, которая бы отслеживала порядок гоблинов в очереди.
В первой строке входных данный записано число \(N\) (\(1\le N\le 10^5\)) - количество запросов к программе. Следующие \(N\) строк содержат описание запросов в формате:
Для каждого запроса типа "-" программа должна вывести номер гоблина, который должен зайти к шаманам.
7 + 1 + 2 - + 3 + 4 - -
1 2 3
Дана лекционная аудитория, в которой несколько профессоров хотят прочесть свои лекции. Для составления расписания профессора подали заявки, вида [\(s_i, f_i\)) – время начала и конца лекции. Лекция считается открытым полуинтервалом, то есть какая-то лекция может начаться в момент окончания другой, без перерыва. Составьте расписание занятий так, чтобы выполнить максимальное количество заявок.
В первой строке вводится натуральное число \(N\), не более 1000 – общее количество заявок. Затем вводится \(N\) строк с описаниями заявок - по два числа в каждом \(s_i\) и \(f_i\).
Гарантируется, что \(s_i < f_i\). Время начала и окончания лекции – натуральное число, не превышает 1440 (в минутах с начала суток :) )
Выведите одно число – максимальное количество заявок, которые можно выполнить.
Во втором примере можно выполнить вторую и третью заявки.
1 5 10
1
3 1 5 2 3 3 4
2
В некоей воинской части есть сапожник. Рабочий день сапожника длится \(N\) минут. Заведующий складом оценивает работу сапожника по количеству починенной обуви, независимо от того, насколько сложный ремонт требовался в каждом случае. Дано \(k\) сапог, нуждающихся в починке. Определите какое максимальное количество из них сапожник сможет починить за один рабочий день.
В первой строке вводятся число \(N\) (натуральное, не превышает 1000), и число \(k\) (натуральное, не превышает 500). Затем идет \(k\) чисел – количество минут, которые требуются чтобы починить \(i\)-й сапог (времена – натуральные числа, не превосходят 100).
Выведите единственное число – максимальное количество сапог, которые можно починить за один рабочий день.
В первом примере можно починить либо первый и второй, либо второй и третий сапоги.
10 3 6 2 8
2
3 2 10 20
0
100 4 2 6 7 8
4