Темы --> Информатика --> Алгоритмы --> Алгоритмы на графах
    Кратчайшие пути в графе(116 задач)
    Обход в глубину(100 задач)
    Способы задания графа(54 задач)
    Минимальный каркас(12 задач)
    Потоки(21 задач)
    Паросочетания(17 задач)
    Эйлеров цикл(9 задач)
    Деревья(16 задач)
---> 319 задач <---
Источники
    Личные олимпиады(938 задач)
    Командные олимпиады(684 задач)
Страница: << 17 18 19 20 21 22 23 >> Отображать по:
#724
Берляндия атакует
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

В этой задаче Вам вновь придется помочь Берляндии. Эта страна состоит из \(n\) городов, некоторые пары из которых соединены двусторонними дорогами, каждая дорога характеризуется своей длиной. Все города пронумерованы числами от 1 до \(n\), столица имеет номер 1. Время от време ни Президент объезжает страну, посещая города страны. Целью каждой поездки является один из городов, к которому он едет из столицы вдоль дорог одним из кратчайших путей.

В далекие времена (когда задачи на алгоритм Дейкстры вызывали сложность) специальное ведомство составила такой набор дорог \(T\), вдоль которого можно было проехать из столицы в любой город, причем единственным образом. Разумеется, путь по дорогам из набора \(T\) из столицы в каждый город являлся кратчайшим. Особо умные жители страны попросту называли этот набор дорог "деревом кратчайших путей". Известно, что Президент пользовался дорогами из \(T\) во время своих поездок. За прошедшие годы этот набор перестал быть секретным, и, поэтому, стал объектом повышенного внимания берляндских экстремистов. У специального ведомства новое задание. Для каждого города кроме столицы необходимо вычислить кратчайшее расстояние до него, при условии, что та дорога по которой Президент должен был закончить свой путь в этот город является атакованной и проезжать по ней нельзя.

Входные данные

В первой строке входного файла записана пара целых чисел \(n\) и \(m\) (\(2 \leq n \leq 4\,000\); \( n - 1 \leq m \leq 100\,000\)), где \(n\) — количество городов в стране, а \(m\)— количество дорог в этой стране. Далее в \(m\) строках содержатся описания дорог, по одной дороге в строке. Каждая дорога задается четверкой целых чисел \(a_j\), \(b_j\), \(l_j\), \(t_j\) , где \(a_j\), \(b_j\) это номера городов, соединяемых дорогой (\(1 \leq a_j, b_j \leq n\); \(a_j \neq b_j\)), \(l_j\) — ее длина (\(1 \leq l_j \leq 10^5\)), а \(t_j\) равно 1 если дорога принадлежит дереву кратчайших путей и 0 в противном случае.

Гарантируется, что набор \(T\) удовлетворяет описанным выше свойствам. Между парой городов может быть более одной дороги. Все дороги двусторонние.

Выходные данные

Выведите \(n - 1\) число в строку через пробелы. \(i\)-ое число должно быть равно либо длине кратчайшго пути из столицы в город \(i + 1\), при условии, что по той дороге из \(T\), которой Президент заканчивал свой путь в этот город, передвигаться нельзя, либо -1, если добраться до города \(i + 1\) вообще невозможно.

Примеры
Входные данные
5 9
3 1 3 1
1 4 2 1
2 1 6 0
2 3 4 0
5 2 3 0
3 2 2 1
5 3 1 1
3 5 2 0
4 5 4 0
Выходные данные
6 7 8 5
#727
Квас
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

На тропическом острове в разгар туристического сезона особой популярностью пользуется квас. Раньше весь квас импортировался из России, но с увеличением популярности этого напитка встал вопрос о производстве кваса прямо на месте. На острове расположено N курортных городов, все города расположены на побережье. Вдоль побережья проходит единственная на острове кольцевая дорога, соединяющая все города. Движение по дороге возможно в любом направлении. Для каждого города известно, сколько бочек кваса требуется ему ежедневно.

Планируется построить всего один завод в каком-нибудь городе, и развозить продукцию по остальным городам. Перевозка одной бочки в соседний город стоит один тугрик (местная валюта).

Ваша задача состоит в том, чтобы определить, в каком из городов следует построить завод, чтобы минимизировать транспортные расходы.

Входные данные

Первая строка входных данных содержит число N – количество городов ( N ≤ 10) и еще N чисел – количество кваса, требуемое ежедневно 1-м, 2-м, …, N -м городом (города нумеруются подряд вдоль кольцевой дороги).

Выходные данные

Выведите одно число – номер города, в котором следует построить завод. Если подходящих городов окажется несколько – выведите номер любого из них.

Задача Е, рис. 4Примеры

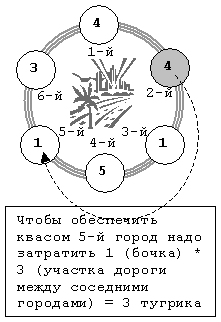
Пояснение для второго примера(см. рисунок):

На острове 6 городов, потребность каждого города указана в кружочках, номер города рядом с кружочком.

Если построить завод во 2-м городе (он выделен серым), то потребуется заплатить 4 + 1 (стоимость перевозки в 1-й и 3-й города) + 5*2 + 3*2 (в 4-й и 6-й) + 1*3 (в 5-й см. рисунок).
Во 2-й вообще ничего не везем. Это будет 24 тугрика. Легко проверить, что если построить завод в других городах, сумма будет больше. Например, если построить в 4-м городе, то сумма составит 1 + 1 + 3*2 + 4*2 + 4*3 = 28 тугриков.

Примеры
Входные данные
3 5 3 10
Выходные данные
3
Входные данные
6 4 4 1 5 1 3
Выходные данные
2
#858
Свинки-копилки
  
Подсчет количества циклов в графе, где у каждой вершины ровно одно исходящее ребро.

У Васи есть N свинок-копилок, свинки занумерованы числами от 1 до N. Каждая копилка может быть открыта единственным соответствующим ей ключом или разбита.

Вася положил ключи в некоторые из копилок (он помнит, какой ключ лежит в какой из копилок). Теперь Вася собрался купить машину, а для этого ему нужно достать деньги из всех копилок. При этом он хочет разбить как можно меньшее количество копилок (ведь ему еще нужно копить деньги на квартиру, дачу, вертолет…). Помогите Васе определить, какое минимальное количество копилок нужно разбить.

Входные данные

В первой строке содержится число N — количество свинок-копилок (1≤N≤100000). Далее идет N строк с описанием того, где лежит ключ от какой копилки: в i-ой из этих строк записан номер копилки, в которой находится ключ от i-ой копилки.

Выходные данные

Выведите единственное число: минимальное количество копилок, которые необходимо разбить.

Пример

Входные данные

Выходные данные

Комментарий

4

2

1

2

4

2

Ключи от первой и третьей копилки лежат в копилке 2, ключ от второй — в первой, а от четвертой — в ней самой.

Чтобы открыть все копилки, достаточно разбить, например, копилки с номерами 1 и 4.
#859
Трехцветные таблицы
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Прямоугольную таблицу, состоящую из N строк и M столбцов, раскрашивают следующим образом. Каждый столбец таблицы и каждую строку красят либо в синий, либо в желтый цвет. В итоге клетки, оказавшиеся на пересечении синего столбца и синей строки оказываются синими, желтого столбца и желтой строки — желтыми, а клетки на пересечении синего столбца и желтой строки, или, наоборот, желтого столбца и синей строки — зелеными.

Раскраска всех клеток таблицы (или просто сама таблица) называется правильной, если она может быть получена описанным выше способом.

Вам дана прямоугольная таблица, которую нужно раскрасить таким образом. Про некоторые клетки известно, какого цвета они должны быть, а остальные клетки могут в итоге быть любого цвета. Определите, сколько существует различных правильных таблиц, в которых нужные клетки покрашены в нужный цвет.

Входные данные

Вводятся числа N и M — количество строк и столбцов таблицы (1≤N≤30, 1≤M≤30). Далее записано N строк по M чисел в каждой, задающие цвета, в которые должны быть окрашены клетки:

0 — клетка может в итоге быть любого цвета

1 — клетка должна быть синей

2 — клетка должна быть желтой

3 — клетка должна быть зеленой

Выходные данные

Выведите одно число — количество различных правильных таблиц, в которых нужные клетки покрашены в нужный цвет. Обратите внимание, что если два или более способов раскраски столбцов и строк таблицы приводят к одинаковой раскраске самой таблицы, то это нужно считать как один вариант раскраски таблицы (см. пример 2).

Примеры

Входные данные

Выходные данные

3 4

1 0 0 0

3 0 0 0

0 0 0 0

16

2 2

3 3

3 3

1

2 2

2 2

2 3

0
#865
Свинки-копилки
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
Задан ориентированный граф, в котором у каждой вершины существует ровно одно исходящее ребро. Требуется найти количество циклов в нем.

У Васи есть N свинок-копилок, свинки занумерованы числами от 1 до N. Каждая копилка может быть открыта единственным соответствующим ей ключом или разбита.

Вася положил ключи в некоторые из копилок (он помнит, какой ключ лежит в какой из копилок). Теперь Вася собрался купить машину, а для этого ему нужно достать деньги из всех копилок. При этом он хочет разбить как можно меньшее количество копилок (ведь ему еще нужно копить деньги на квартиру, дачу, вертолет…). Помогите Васе определить, какое минимальное количество копилок нужно разбить.

Входные данные

В первой строке содержится число N — количество свинок-копилок (1≤N≤100). Далее идет N строк с описанием того, где лежит ключ от какой копилки: в i-ой из этих строк записан номер копилки, в которой находится ключ от i-ой копилки.

Выходные данные

Выведите единственное число: минимальное количество копилок, которые необходимо разбить.

Пример

Входные данные

Выходные данные

Комментарий

4

2

1

2

4

2

Ключи от первой и третьей копилки лежат в копилке 2, ключ от второй — в первой, а от четвертой — в ней самой.

Чтобы открыть все копилки, достаточно разбить, например, копилки с номерами 1 и 4.
Страница: << 17 18 19 20 21 22 23 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест