Темы --> Информатика --> Алгоритмы --> Алгоритмы на графах
    Кратчайшие пути в графе(116 задач)
    Обход в глубину(100 задач)
    Способы задания графа(54 задач)
    Минимальный каркас(12 задач)
    Потоки(21 задач)
    Паросочетания(17 задач)
    Эйлеров цикл(9 задач)
    Деревья(16 задач)
---> 319 задач <---
Источники
    Личные олимпиады(938 задач)
    Командные олимпиады(684 задач)
Страница: << 24 25 26 27 28 29 30 >> Отображать по:
#1335
Столовая
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Сегодня у студентов праздник! В одном из новых зданий университета решили открыть столовую. Для этих целей требуется выбрать одно из зданий, в котором и будет располагаться столовая. Чтобы студенты как можно меньше отвлекались от учёбы, было решено выбрать такое здание, чтобы максимальное расстояние от него до всех остальных зданий было как можно меньше.

Помогите найти такое здание!

Входные данные

В первой строке находятся два числе \(N\) и \(M\) - количество зданий и количество дорог, соединяющих здания (\(1 \le N \le 100, 0 \le M \le \frac{N \cdot (N-1)}{2}\)). Далее в \(M\) строках расположены описания дорог: 3 целых числа \(s_i\), \(e_i\), \(l_i\) - здания, в которых начинается и заканчивается дорога и длина дороги соответственно (\(1 \le s_i, e_i \le N, 0 \le l_i \le 100\), дороги двунаправленные).

Выходные данные

Необходимо вывести одно число - номер искомого здания. Если есть несколько зданий удовлетворяющих поставленным критериям, выберите среди них здание с наименьшим номером.

Примеры
Входные данные
3 2
1 2 1
2 3 2
Выходные данные
2
Входные данные
3 1
1 2 10
Выходные данные
1
#1336
Опасный маршрут
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Профессор Флойд живёт в очень опасном районе города. Ежедневно бандиты грабят на улицах прохожих. Читая криминальную хронику, профессор Флойд вычислил вероятность быть ограбленным при проходе по каждой улице города.

Теперь он хочет найти наиболее безопасный путь от дома до университета, в котором он преподаёт. Иными словами, он хочет найти путь от дома до университета, для которого вероятность быть ограбленным минимальна.

Входные данные

В первой строке находятся два числа \(N\) и \(M\) - количество зданий и количество улиц, соединяющих здания (\(1 \le N \le 100, 1 \le M \le \frac{N \cdot (N-1)}{2}\)). В следующей строке находятся числа \(S\) и \(E\) -- номер дома, в котором живёт профессор и номер дома, в котором находится университет соответственно. Далее в \(M\) строках расположены описания дорог: 3 целых числа \(s_i, e_i, p_i\) - здания, в которых начинается и заканчивается дорога и вероятность в процентах быть ограбленным, пройдя по дороге соответственно (\(1 \le s_i, e_i \le N, 0 \le p_i \le 100\), дороги двунаправленные). Гарантируется, что существует хотя бы один путь от дома профессора до университета.

Выходные данные

Необходимо вывести одно число - минимальную возможную вероятность быть ограбленным. Выведите ответ с максимально возможной точностью.

Примеры
Входные данные
3 3
1 3
1 2 20
1 3 50
2 3 20
Выходные данные
0.36
#1337
Компьютерная сеть
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes

Для проведения олимпиады школьников по информатике требуется соединить компьютеры в сеть. Организаторы олимпиады разработали схему соединения компьютеров. В соответствии с этой схемой некоторые пары компьютеров должны быть соединены кабелем, и сигнал сможет дойти по кабелям от любого компьютера до любого другого, возможно, через другие компьютеры.

Некоторые компьютеры могут быть соединены циклически. Цикл называется простым, если каждый компьютер из этого цикла соединён ровно с двумя другими компьютерами этого цикла, и в этот цикл никакой кабель не входит более одного раза. Некоторые кабели могут не входить ни в какой цикл.

Известно, что в разработанной схеме никакой кабель не принадлежит двум простым циклам одновременно.

Организаторам олимпиады поручено разместить компьютеры в зале соревнований. При размещении должны выполняться следующие условия:

1.Компьютеры размещаются на плоскости в точках с целочисленными координатами.

2.Координаты компьютеров x и y лежат в диапазоне 0 ≤ x, y ≤ 106.

3.Никакие два компьютера не располагаются в одной точке.

4.Кабели являются отрезками прямых.

5.Кабели не пересекаются между собой и не проходят через точки размещения компьютеров, к которым они не подключены.

Требуется написать программу, выполняющую размещение компьютеров по заданному описанию схемы.

Входные данные

В первой строке входного файла содержатся числа N и M — количество компьютеров и количество кабелей в схеме (1 ≤ N ≤ 100 000, 0 ≤ M ≤ 200 000). В последующих M строках содержатся пары чисел, разделенных пробелами. Каждая такая пара описывает один кабель, числа представляют собой номера соединенных компьютеров. Компьютеры пронумерованы от 1 до N. Никакая пара не встречается дважды, и никакой кабель не соединяет компьютер с самим собой.

Выходные данные

Выходной файл должен содержать N строк. Строка с номером i должна содержать координаты i-го компьютера, разделенные пробелом. Сначала выводится координата x, затем y. Разрешается вывести любой вариант размещения компьютеров, при котором выполняются условия 1–5.

Примечания

Решения, корректно работающие при отсутствии циклов, будут оцениваться из 40 баллов.

Решения, корректно работающие при наличии только одного цикла, будут оцениваться из 60 баллов.

Пример входных и выходных данных

Ввод

 Вывод

13 14

11 12

11 13

1 3

3 5

5 8

8 9

8 6

6 3

4 6

4 2

6 10

10 11

10 7

7 4

1 0

3 0

1 1

3 1

0 2

2 2

4 2

1 3

1 4

3 3

3 4

2 5

4 5


#1355
Векторы
  

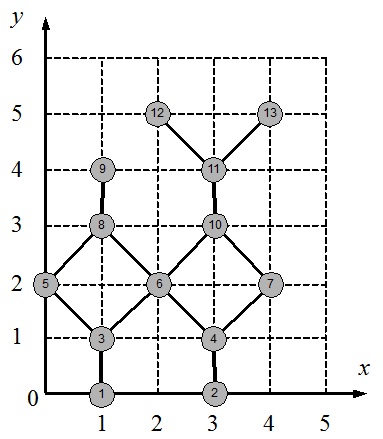
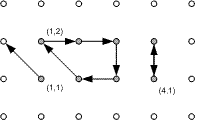На плоскости задано множество точек (x, y), где x, y – целые числа, 1≤x≤M, 1≤y≤N. Из каждой точки выходит ровно один из следующих векторов: (-1,-1), (-1,0), (-1,1), (0,1), (1,1), (1,0), (1,-1), (0,-1). Каждый вектор соединяет одну целочисленную точку плоскости с другой. Например, если из точке (2, 5) выходит вектор (1, 1), то он соединяет эту точку с (3, 6), но не наоборот.

Последовательность из двух и более точек плоскости a1, a2,…, ak назовем циклом, если каждая точка ai соединена вектором с ai+1 (1≤i≤k-1), и ak соединена вектором с a1. Циклы считаются разными если они отличаются хотя бы одной вершиной.

Напишите программу, которая по информации о векторах, выходящих из точек плоскости, находит количество различных циклов.

Входные данные

Первая строка входного файла содержит два целых числа N (1≤N≤100) и M (1≤M≤100). Каждая из последующих N строк, содержит M пар чисел (т.е. 2≤M чисел). Пара x, которая находится в строке y, задает вектор в точке (x, y).

Выходные данные

Единственная строка выходного файла должна содержать целое число – количество циклов, образованных векторами.

Примеры
Входные данные
2 4 
-1 1 -1 1 -1 0 0 1
1 0 1 0 0 -1 0 -1
Выходные данные
2
#1377
Остовное дерево
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Требуется найти в связном графе остовное дерево минимально веса.

Входные данные

Первая строка входного файла содержит два натуральных числа n и m - количество вершин и ребер графа соответственно (1≤n≤20000, 0≤m≤100000). Следующие m строк содержат описание ребер по одному на строке. Ребро номер i описывается тремя натуральными числами bi, ei и wi - номера концов ребра и его вес соответственно (1≤bi,ei≤n, 0≤wi≤100000).

Граф является связным.

Выходные данные

Выведите единственное целое число - вес минимального остовного дерева.

Примеры
Входные данные
4 4
1 2 1
2 3 2
3 4 5
4 1 4
Выходные данные
7
Страница: << 24 25 26 27 28 29 30 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест