Темы --> Информатика --> Алгоритмы --> Алгоритмы на графах
    Кратчайшие пути в графе(116 задач)
    Обход в глубину(100 задач)
    Способы задания графа(54 задач)
    Минимальный каркас(12 задач)
    Потоки(21 задач)
    Паросочетания(17 задач)
    Эйлеров цикл(9 задач)
    Деревья(16 задач)
---> 319 задач <---
Источники
    Личные олимпиады(938 задач)
    Командные олимпиады(684 задач)
Страница: << 40 41 42 43 44 45 46 >> Отображать по:
#3366
Дятлы
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
Необходимо проверить отсутствие циклов

В парке растут два очень высоких дерева, на стволе каждого из которых расположены дупла одно под другим на равном расстоянии друг от друга. Однажды N дятлов решили заселить эти дупла. Некоторые из них знакомы и поэтому хотели бы иметь возможность летать друг к другу в гости. Дятлы летают прямолинейно и очень быстро. Чтобы уменьшить вероятность столкновения, они решили селиться по следующему принципу:

Каждые две дятла, которые хотят летать друг к другу в гости, должны жить на разных деревьях Отрезки, соединяющие дупла знакомых между собой дятлов не пересекаются (однако их концы могут совпадать).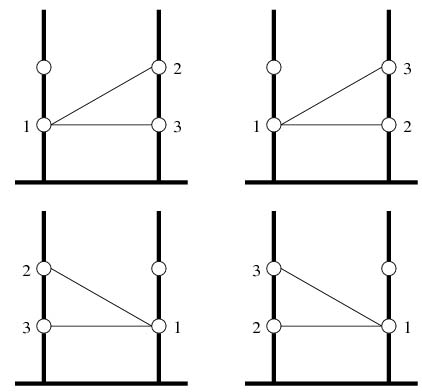

Кроме того, дятлы хотят жить как можно ниже, т.е. на каждом из деревьев они занимают дупла подряд, начина снизу. На каждом из деревьев больше дупел, чем общее количество дятлов.
Как известно, у дятлов очень маленький мозг. Поэтому вам следует подумать за них и сообщить, сколькими способами они могут разместиться в дуплах. Т.к. дятлы также плохо воспринимают большие числа, ответ следует вывести по модулю K.

Входные данные

В первой строке содержатся три числа: \(N\) – количество дятлов (\(1 \leq N \leq 10^6\)), \(M\) – количество пар знакомых дятлов (\(1 \leq M \leq 10^7\)) и число \(K\) (\(1 \leq K \leq 2\times 10^6\)). Дятлы занумерованы от \(1\) до \(N\). В следующих \(M\) строках заданы два числа \(a_i\) и \(b_i\) (\(1 \leq a_i, b_i \leq N\)), задающие пару знакомых дятлов.

Выходные данные

Вывод должен содержать одно число: количество вариантов размещения по модулю K.

Примеры тестов

Примеры
Входные данные
3 2 10
1 2
1 3
Выходные данные
4
Входные данные
4 4 17
1 2
1 3
4 2
3 4
Выходные данные
0
#3373
Печатная схема
  
ограничение по времени на тест
0.1 second;
ограничение по памяти на тест
64 megabytes

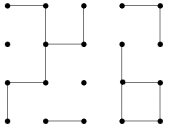Печатной схемой называется плоская поверхность содержащей узлы и перемычки, соединяющие пары узлов. Мы будем рассматривать печатные схемы специального вида, где все узлы расположены в узлах прямоугольной сетки, а перемычки (вертикальные или горизонтальные) соединяют пары соседних узлов. Печатная схема называется связной, если любые два узла соединены друг с другом последовательностью перемычек. На вход дается печатная схема, где некоторые соседние узлы уже соединены перемычками. К ней необходимо добавить некоторое количество перемычек таким образом, чтобы схема стала связной. Стоимость вертикальной перемычки – 1, а горизонтальной – 2.
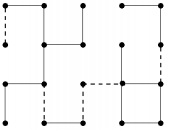Ваша программа должна по начальной печатной схеме определить количество добавляемых перемычек, минимальную стоимость такого добавления, а также вывести сами добавляемые перемычки.

Входные данные

Первая строка входного файла содержит два натуральных числа \(N\) и \(M\) – количество строк (\(1 \leq N \leq 100\)) и количество столбцов (\(1 \leq M \leq 100\)) соответственно. Каждый узел определяется своими координатами, нумерация начинается с верхнего левого угла (координаты (\(1\), \(1\))). Далее дается описание решетки в виде \(N\) строк по \(M\) чисел. Каждое число обозначает связь узла (\(i\), \(j\)) с узлами (\(i+1\), \(j\)) и (\(i\), \(j+1\)) в следующем формате: \(0\) – узел (\(i\), \(j\)) не соединен ни с одним из узлов (\(i+1\), \(j\)) и (\(i\), \(j+1\)). \(1\) – узел (\(i\), \(j\)) соединен только с узлом (\(i+1\), \(j\)) \(2\) – узел (\(i\), \(j\)) соединен только с узлом (\(i\), \(j+1\)) \(3\) – узел (\(i\), \(j\)) соединен и с узлом (\(i+1\), \(j\)), и с узлом (\(i\), \(j+1\)).

Выходные данные

Первая строка должна содержать два числа \(K\) и \(V\) – количество добавленных перемычек и стоимость добавления соответственно. Каждая из следующих \(K\) строк должна содержать описание добавленной перемычки в формате \(i\), \(j\), \(d\), где (\(i\), \(j\)) – координаты начального узла, а \(d\) может принимать значения \(1\) или \(2\). \(d = 1\) обозначает, что соединены узлы (\(i\), \(j\)) и (\(i+1\), \(j\)), \(d = 2\) – узлы (\(i\), \(j\)) и (\(i\), \(j+1\)). Если решений несколько – выведите любое из них.

Примеры
Входные данные
4 5
2 1 1 2 1
0 3 0 1 0
3 0 0 3 1
0 2 0 2 0
Выходные данные
5 6
1 1 1
2 3 1
3 3 1
4 3 2
2 5 1
#3376
Кратчайший путь
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Дан ориентированный взвешенный граф.
Найдите кратчайшее расстояние от одной заданной вершины до другой.

Входные данные

В первой строке входного файла два числа: N и M (1 ≤ N ≤ 100, 1 ≤ M ≤ 10000), где N - количество вершин графа, а M - количество ребер.
В следующей строке заданы числа S и F - начальная и конечная вершины.

Далее следует \(M\) троек чисел Ai, Bi, Ti (1 ≤ Ti ≤ 10) - номера вершин соединенных ребром и вес данного ребра.

Выходные данные

Вывести искомое расстояние или -1, если пути между указанными вершинами не существует.

Примеры
Входные данные
3 6
2 1
1 2 1
1 3 1
2 1 4
2 3 1
3 1 2
3 2 1
Выходные данные
3
#3377
Лесопосадки
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Дан неориентированный невзвешенный граф. Необходимо определить, является ли он деревом.

Входные данные

В первой строке входного файла содержится одно натуральное число N (N ≤ 100) -- количество вершин в графе. Далее в N строках по N чисел -- матрица смежности графа: в i-ой строке на j-ом месте стоит 1, если вершины i и j соединены ребром, и 0, если ребра между ними нет. На главной диагонали матрицы стоят нули. Матрица симметрична относительно главной диагонали.

Выходные данные

Вывести YES, если граф является деревом, NO иначе.

Примеры
Входные данные
2
0 1
1 0
Выходные данные
YES
Входные данные
5
0 1 0 0 0
1 0 0 0 1
0 0 0 0 1
0 0 0 0 0
0 1 1 0 0
Выходные данные
NO
#3381
Коровники
  

В селе Максоярославке коровы обычно пасутся на лужайках, соединенных дорожками, на каждой лужайке пасется хотя бы одна корова. При этом для каждой пары лужаек есть ровно один способ пройти от одной лужайки до другой. По каждой дорожке можно двигаться в обоих направлениях. Считается, что все дорожки имеют одинаковую длину.
Главный фермер села хочет построить на лужайках \(k\) коровников для своих коров. Ясно, что каждая корова вечером будет возвращаться именно в тот коровник, который ближе к ее лужайке (если расстояние до коровников одинаково, то в любой из них). Поэтому возникает задача определения такого расположения коровников, при котором наибольшее из расстояний, проходимых коровами, было бы минимально.

Входные данные

В первой строке входного файла содержатся два числа \(n\) и \(k\) (\(2 \le n \le 50\;000\), \(1 \le k \le n\)) --- количество лужаек и планируемое число коровников, соответственно. Следующие \(n - 1\) строк содержат описания дорожек. Каждая дорожка задается парой целых положительных чисел (\(a, \, b\)), где \(a\) и \(b\) --- номера лужаек, которые соединяет данная дорожка. Лужайки нумеруются с единицы.

Выходные данные

В первой строке входного файла выведите \(l\) --- максимальное количество дорожек, по которым придется пройти корове, чтобы попасть в коровник. Во второй строке выведите \(k\) различных целых чисел --- номера лужаек, на которых следует построить коровники. Если оптимальных решений несколько, разрешается вывести любое из них.

Примеры
Входные данные
7 2
5 4
4 3
1 3
2 3
4 6
6 7
Выходные данные
2
1 4
Страница: << 40 41 42 43 44 45 46 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест