Темы --> Информатика --> Алгоритмы --> Алгоритмы на графах
    Кратчайшие пути в графе(116 задач)
    Обход в глубину(100 задач)
    Способы задания графа(54 задач)
    Минимальный каркас(12 задач)
    Потоки(21 задач)
    Паросочетания(17 задач)
    Эйлеров цикл(9 задач)
    Деревья(16 задач)
---> 319 задач <---
Источники
    Личные олимпиады(938 задач)
    Командные олимпиады(684 задач)
Страница: << 47 48 49 50 51 52 53 >> Отображать по:
#111663
Доминошахматы
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Вася очень любит различные игры: шашки, шахматы, домино, крестики-нолики и т. д. Поскольку он играет в них уже достаточно давно, он успел изучить эти игры достаточно хорошо, и они стали скучными. Поэтому он теперь изобретает новые игры на основе тех, в которые уже наигрался. Недавно он изобрел игру «Доминошахматы».

Она состоит в следующем: Вася берет у дедушки большой кусок фанеры и раскрашивает его так, что у него получается шахматная доска размера N × M клеточек. Потом он берет кости домино и пытается покрыть ими полученную доску так, чтобы все клеточки были закрыты, не было наложений и никакие доминошки не торчали за края доски (каждая доминошка покрывает две соседние клетки).

Поскольку Вася не спрашивает разрешения у дедушки прежде, чем взять доску, он иногда берет ненужные доски, а иногда и те, которые дедушка хотел использовать в строительстве новой дачи. Как раз сегодня Вася взял «нужную» доску, поэтому дедушка был вынужден вырезать из Васиной доски два квадрата по одной клеточке.

Вася сначала огорчился, что не сможет поиграть в свою игру. А потом решил попробовать замостить доску с уже вырезанными клетками, причем так, чтобы вырезанные клетки не были накрыты доминошками.

Помогите Васе понять, можно ли это сделать.

Входные данные

В первой строке входных данных записаны числа N и M — размеры доски (1 ≤ N ≤ 200, 1 ≤ M ≤ 200, N·M > 2).

Во второй строке вводятся через пробел два целых числа — координаты x1 и y1 первой вырезанной клетки (1 ≤ x1 ≤ N, 1 ≤ y1 ≤ M).

В третьей строке вводятся через пробел два целых числа — координаты x2 и y2 второй вырезанной клетки (1 ≤ x2 ≤ N, 1 ≤ y2 ≤ M).

Первая и вторая клетки не совпадают.

Выходные данные

Выведите «YES», если доску с вырезанными клеточками можно покрыть доминошками, и «NO» в противном случае. (Запас доминошек у Васи бесконечный.)

Примеры
Входные данные
2 2
1 1
2 2
Выходные данные
NO
Входные данные
2 2
1 1
1 2
Выходные данные
YES
#111701
Секрет
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
128 megabytes

В городском управлении милиции одного прибрежного города ведется расследование крупного дела, в котором могут быть замешаны сотрудники милиции. Было принято решение о тайной установке оборудования для просмотра информации, поступающей через Интернет. Под подозрение попадают два отдела, но добиться выделения денег на покупку двух комплектов оборудования не удалось. К счастью, внутренняя сеть управления имеет древовидную структуру, то есть каждый отдел имеет выход в Интернет через какой-либо другой отдел. Исключение составляет отдел по борьбе с компьютерными преступлениями, который имеет непосредственный доступ в Интернет по модемной линии.

Можно было бы установить оборудование для слежения прямо в этом отделе, но лучше найти такое расположение, чтобы нарушалась секретность как можно меньшего количества лишних отделов. Решение этой задачи поручили вам.

Подчиненные уже пронумеровали все отделы числами натуральными числами, начиная с 1, первый номер присвоен отделу по борьбе с компьютерными преступлениями.

Входные данные

Первая строка входного файла содержит натуральное число n (n ≤ 30000) — количество отделов. Во второй строке записаны номера отделов, за которыми необходимо установить слежение. На третьей строке находятся n - 1 натуральных чисел, i-е из них не больше i и задает номер отдела, к которому подсоединен отдел i + 1.

Выходные данные

В выходной файл выведите одно число — номер отдела, в котором следует установить следящее оборудование.

Примеры
Входные данные
4
3 4
1 1 3
Выходные данные
3
Входные данные
8
3 6
1 1 2 4 5 1 1
Выходные данные
1
#111710
Дороги
  
ограничение по времени на тест
0.5 second;
ограничение по памяти на тест
64 megabytes

Мэр города Гадюкино решил проверить состояние дорог после только что проведенного капитального ремонта. Для этого он хочет проехать по каждой дороге в обоих направлениях.

Помогите мэру составить кратчайший маршрут, проходящий по каждой дороге в каждом направлении хотя бы один раз.

Входные данные

В городе Гадюкино n перекрестков и m дорог, каждая из которых соединяет два различных перекрестка. Между двумя перекрестками может быть не более одной дороги.

Известно, что по дорогам от каждого перекрестка можно доехать до любого другого.

Входной файл содержит целые числа n и m (1 ≤ n ≤ 104, 1 ≤ m ≤ 105), и далее m пар целых чисел ai и bi — номера перекрестков, которые соединяет i-я дорога.

Выходные данные

Выведите число s — минимальную длину пути и далее s + 1 число — номера перекрестков в том порядке, в котором их нужно проезжать.

Примеры
Входные данные
3 3
1 2
2 3
1 3
Выходные данные
6
1 3 2 1 2 3 1
#111711
Dynamic LCA
  

Постановка задачи о {Наименьшем общем предке} такова: дано дерево T с выделенным корнем и две вершины u и v, lca(u, v) - вершина с максимальной глубиной, которая является предком и u, и v. Например, в картинке внизу lca(8, 7) - вершина 3.

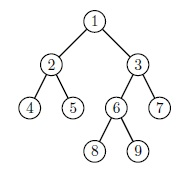
С помощью операции chroot(u) мы можем менять корень дерева, достаточно отметить u, как новый корень, и направить ребра вдоль пути от корня. Наименьшие общие предки вершин поменяются соответствующе. Например, если мы сделаем chroot(6) на картинке сверху, lca(8, 7) станет вершина 6. Получившееся дерево изображено снизу.

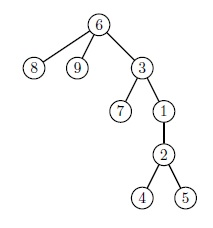
Вам дано дерево T. Изначально корень этого дерева - вершина 1. Напишите программу, которая поддерживает эти две операции: lca(u, v) и chroot(u).

Входные данные

Входной файл состоит из нескольких тестов.

Первая строка каждого теста содержит натуральное число n  — количество вершин в дереве (1 ≤ n ≤ 100 000). Следующие n - 1 строки содержат по 2 натуральных числа и описывают ребра дерева. Далее идет строка с единственным натуральным числом m — число операций —. Следующие m строк содержат операции. Строка "? u v" означает операцию lca(u, v), a строка "! u" - chroot(u). Последняя строка содержит число 0.

Сумма n для всех тестов не превосходит 100 000. Сумма m для всех тестов не превосходит 200 000.

Выходные данные

Для каждой операции "? u v" выведите значение lca(u, v). Числа разделяйте переводами строк.

Система оценки:

Система тестов состоит из двух групп:

Первая группа состоит из тестов, для которых выполняется ограничение \(n \le 100\), \(m \le 10000\). За прохождение всех тестов группы ставится 55 баллов.

Вторая группа стоит из тестов, в которых нет дополнительных ограничений. За прохождение тестов этой группы и всех предыдущих тестов ставится дополнительно 45 баллов.

Примеры
Входные данные
9
1 2
1 3
2 4
2 5
3 6
3 7
6 8
6 9
10
? 4 5
? 5 6
? 8 7
! 6
? 8 7
? 4 5
? 4 7
? 5 9
! 2
? 4 3
0
Выходные данные
2
1
3
6
2
3
6
2
#111723
Network Instability
  

Вася устроился сисадмином в крупную и известную компанию Проблемсофт. В сети компании n компьютеров, некоторые пары которых соединены кабелем напрямую. Всего таких соединений m, причем Вася весьма неплохой администратор, так что никакой кабель не соединяет компьютер с самим собой и каждая пара компьютеров соединена не более чем одним кабелем.

На каждом компьютере в фирме Проблемсофт установлена специальная программа разработанная и поддерживаемая инженерами Проблемсофта, под названием ЗлойЖук. Инженеры этой компании отличаются крайним трудолюбием и высокой производительностью, в связи с чем новые версии программы ЗлойЖук выходят почти ежедневно. Однако, не все сотрудники компании разделяют трудолюбие инженеров, поэтому обновляют программу ЗлойЖук неохотно, и всякий раз до какой-то случайной версии (вполне могут "обновить" до такой же или даже более старой).

После нескольких ужасных месяцев, в течение которых исправлять различные ошибки приходилось днями и ночами, без обедов и выходных, Вася понял в чем причина подавляющего большинства всех сбоев! Причина в том, что компьютеры пересылающие данные по соединяющему их кабелю могут иметь различные версии программы ЗлойЖук. Прямое соединение кабелем двух компьютеров с различными версиями программы ЗлойЖук Вася называет нестабильным.

На последнем корпоративе компании Проблемсофт Вася вместо развлечений ходил с листочком и узнавал у каждого сотрудника когда он планирует обновить программу ЗлойЖук и до какой версии. Нельзя сказать, чтобы коллеги охотно отвечали на эти вопросы, вместо того что купаться в джакузи и пить Кока-Колу, но все-таки Вася смог составить график планируемых изменений версий программы ЗлойЖук на всех компьютерах сети Проблемсофта. Теперь его интересует количество нестабильных соединений в сети после выполнения каждого изменения.

Входные данные

Первая строка входного файла содержит два целых числа n и m (1 ≤ n, m ≤ 105).

Вторая строка содержит n целых чисел v1, v2, ..., vn: версии программы ЗлойЖук изначально установленные на компьютерах Проблемсофта (1 ≤ vi ≤ 105).

Следующие m строк содержат числа ai и bi: описание соединений (1 ≤ ai, bi ≤ n, ai ≠ bi). Гарантируется что сеть хорошая, то есть никакая пара компьютеров не соединена более чем одним кабелем и никакой компьютер не соединен кабелем с самим собой.

Следующая строка содержит целое число q: количество запланированных изменений версий программы ЗлойЖук (1 ≤ q ≤ 105).

Далее следуют q строк; i-ая содержит числа ci и v'i: номер компьютера на котором происходит изменение, и номер новой версии программы ЗлойЖук. Изменения даны в хронологическом порядке, никакия два изменения не происходят одновременно.

Выходные данные

Выведите q строк; i-ая строка должна содержать одно целое число: количество нестабильных соединений сразу после выполнения i-го обновления.

Примеры
Входные данные
4 5
1 2 3 4
1 2
2 3
3 4
4 1
1 3
5
1 5
3 2
4 4
1 4
2 3
Выходные данные
5
4
4
3
4
Страница: << 47 48 49 50 51 52 53 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест