Обход в глубину(100 задач)
Способы задания графа(54 задач)
Минимальный каркас(12 задач)
Потоки(21 задач)
Паросочетания(17 задач)
Эйлеров цикл(9 задач)
Деревья(16 задач)
Задано подвешенное дерево, содержащее n (1 ≤ n ≤ 100 000) вершин, пронумерованных от 0 до n - 1. Требуется ответить на m (1 ≤ m ≤ 10 000 000) запросов о наименьшем общем предке для пары вершин. Запросы генерируются следующим образом. Заданы числа a1, a2 и числа x, y и z. Числа a3, ..., a2m генерируются следующим образом: ai = 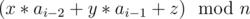 . Первый запрос имеет вид {a1, a2}. Если ответ на (i - 1)-й запрос равен v, то i-й запрос имеет вид {
. Первый запрос имеет вид {a1, a2}. Если ответ на (i - 1)-й запрос равен v, то i-й запрос имеет вид {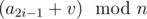 , a2i}.
, a2i}.
Первая строка содержит два числа: n и m. Корень дерева имеет номер 0. Вторая строка содержит n - 1 целых чисел, i-е из этих чисел равно номеру родителя вершины i. Третья строка содержит число содержит два целых числа в диапазоне от 0 до n - 1: a1 и a2. Четвертая строка содержит три целых числа: x, y и z, эти числа неотрицательны и не превосходят 109.
Выведите в выходной файл сумму номеров вершин — ответов на все запросы.
3 2 0 1 2 1 1 1 0
2
В городе N в ближайшее время состоится этап чемпионата мира по автогонкам среди автомобилей класса Формула-0. Поскольку специальный автодром для этих соревнований организаторы построить не успели, было решено организовать трассу на улицах города.
В городе N есть n перекрестков, некоторые пары которых соединены дорогами, движение по которым возможно в обоих направлениях. При этом любые два перекрестка соединены не более чем одной дорогой.
Трасса, на которой будут проводиться соревнования, должна быть круговой (т.е. должна начинаться и заканчиваться на одном и том же перекрестке), при этом в процессе движения по ней никакой перекресток не должен встречаться более одного раза.
На предварительном этапе подготовки оргкомитетом был создан список всех дорог города. Теперь настало время его использовать. Первый вопрос, который необходимо решить, – вопрос о существовании в городе требуемой круговой трассы (разумеется, если ответ будет отрицательным, организаторам придется в срочном порядке построить еще несколько дорог). Единственная проблема заключается в том, что у организаторов есть подозрение, что, поскольку список составлялся не очень внимательно, в нем некоторые дороги указаны больше одного раза.
Напишите программу, которая по заданному списку дорог города определит, возможна ли организация в городе требуемой круговой трассы.
Первая строка входного файла содержит два целых числа: n(1 ≤ n ≤ 1000) – количество перекрестков в городе N и m(0 ≤ m ≤ 100000) – количество дорог в составленном списке.
Последующие m строк описывают дороги. Каждая дорога описывается двумя числами: u и v (1 ≤ u, v ≤ n, u ≠ v) – номерами перекрестков, которые она соединяет. Так как дороги двусторонние, то пара чисел (u;v) и пара чисел (v;u) описывают одну и ту же дорогу.
В выходной файл выведите слово YES, если в городе возможно организовать крговую трассу для соревнований, и слово NO – в противном случае.
3 4 1 2 2 3 3 1 3 2
YES
2 3 1 2 2 1 2 1
NO
Женя недавно купил себе новую соковыжималку. Теперь по утрам он и его братья и сестры пьют свежевыжатый фруктовый сок. А это, между прочим, очень полезно!
Недавно они поняли, что можно пить сок, выжатый не только из одного вида фруктов, как, например, апельсиновый, но и различные смеси, например, виноградно-яблочный.
В Жениной семье все очень любят сок, поэтому могут утром выпить не один стакан, причем разных видов сока. Например, его сестра Катя очень любит грейпфрутовый и апельсиновый соки. Женя, как наиболее технически грамотный человек, каждое утро занимается приготовлением соков.
Опишем подробнее, как работает соковыжималка. В нее загружаются фрукты, они проходят отжим в центрифуге, обезвоженная мякоть сбрасывается в отдельный резервуар, а сок попадает в специальную емкость.
Основная проблема состоит в том, что эту емкость иногда приходится мыть. Например, если после приготовления апельсинового сока, необходимо приготовить яблочный, то емкость надо мыть, иначе получится апельсиново-яблочный сок. Более формально, пусть сок A состоит из компонентов a1, ..., an, а сок B из компонентов b1, ..., bm. Сок B можно готовить после сока A, если любой из компонентов ai является компонентом сока B (т.е. 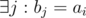 ). В противном случае емкость для сока надо помыть.
). В противном случае емкость для сока надо помыть.
Женя не очень любит мыть посуду, поэтому хочет мыть емкость как можно меньшее число раз. Помогите ему.
Первая строка входного файла содержит количество N различных соков, которые требуется приготовить (1 ≤ N ≤ 300). Каждая из последующих N строк описывает один из соков. Описание сока состоит из числа k его компонентов (1 ≤ k ≤ 300) и списка этих компонентов. Каждый из компонентов сока описывается словом длиной до 30 символов из строчных и прописных букв латинского алфавита. Прописные и строчные буквы различаются. Различные компоненты имеют различные названия.
В выходной файл выведите минимальное количество раз, которое Жене придется помыть емкость для сока. Учитывайте при этом, что емкость для сока надо помыть и после приготовления последней порции сока.
4 1 Apple 2 Apple Orange 1 Orange 2 Orange Pineapple
2
3 1 Apple 1 Orange 1 Mango
3
Группа Pink Floyd собирается дать новый концертный тур по всему миру. По предыдущему опыту группа знает, что солист Роджер Уотерс постоянно нервничает при перелетах. На некоторых маршрутах он теряет вес от волнения, а на других - много ест и набирает вес.
Известно, что чем больше весит Роджер, тем лучше выступает группа, поэтому требуется спланировать перелеты так, чтобы вес Роджера на каждом концерте был максимально возможным. Группа должна посещать города в том же порядке, в котором она дает концерты. При этом между концертами группа может посещать промежуточные города.
Первая строка входного файла содержит три натуральных числа n, m и k - количество городов в мире, количество рейсов и количество концертов, которые должна дать группа соответственно (n≤100, m≤104, 2≤k≤104). Города пронумерованы числами от 1 до n. Следующие m строк содержат описание рейсов, по одному на строке. Рейс номер i описывается тремя числами bi, ei и wi - номер начального и конечного города рейса и предполагаемое изменение веса Роджера в миллиграммах (1≤bi,ei≤n, −105≤wi≤105). Последняя строка содержит числа a1, a2, ..., ak - номера городов, в которых проводятся концерты. В начале концертного тура группа находится в городе a1.Гарантируется, что группа может дать все концерты.
Первая строка выходного файла должна содержать число s - количество рейсов, которые должна сделать группа. Вторая строка должна содержать s чисел - номера используемых рейсов. Не существует такой последовательности маршрутов между концертами, что Роджер будет набирать вес неограниченно.
4 8 5 1 2 -2 2 3 3 3 4 -5 4 1 3 1 3 2 3 1 -2 3 2 -3 2 4 -10 1 3 1 2 4
6 5 6 5 7 2 3
После тысячелетнего правления большей частью Млечного Пути начался окончательный распад КОсмического ОБъединения ОЛигархов на несколько независимых монархий. КОБОЛ является высокоорганизованной империей, которая имеет форму огромного прямоугольного параллепипида n * m * k парсеков. Империя КОБОЛ сильно засекречена, поэтому лишь немногие знают точные значения n, m и k. Для облегчения контроля империя разделена на nmk маленьких владений по одному кубическому парсеку каждое. Эти владения занумерованы следующим образом:
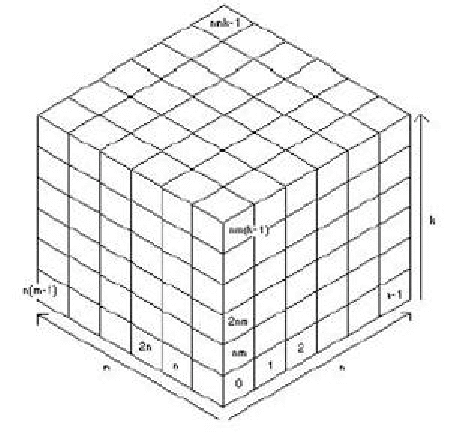
На вход может подаваться сразу несколько тестов. Первая строка содержит положительное целое число - количество тестов. Первая строка каждого отдельного теста содержит четыре целых числа: n m k l, где n, m и k (1 ≤ n, m, k ≤ 30) — размеры империи, а l — количество независимых монархий, на которое должна распасться империя. Далее следуют l строк с описаниями монархий. Каждая из них имеет следующий вид: p d1 d2 ... dp , где p — количество владений, входящих в монархию (1 ≤ p ≤ 20), а d1, ..., dp — номера этих владений. Монархии перечислены в порядке их отделения от империи.
Для каждого теста вы должны на отдельной строке выдать одно целое число — количество месяцев, в течение которых империя будет не связна.
2 2 2 3 9 2 4 5 3 6 8 10 1 7 1 2 1 11 1 9 1 1 1 0 1 3 2 2 3 3 4 0 1 2 3 4 4 5 6 7 4 8 9 10 11
4 0