Обход в глубину(100 задач)
Способы задания графа(54 задач)
Минимальный каркас(12 задач)
Потоки(21 задач)
Паросочетания(17 задач)
Эйлеров цикл(9 задач)
Деревья(16 задач)
Охотник Боб часто гуляет со своей собакой Ральфом. Боб гуляет с постоянной скоростью и его путь ломаная (возможно, самопересекающаяся), каждая вершина которой задается двумя целыми числами (Xi, Yi) декартовыми координатами.
Ральф бегает сам по себе, но обязательно должен встречаться с хозяином в указанных N точках. Собака начинает свой путь одновременно с хозяином в точке (X1, Y1) и завешает его вместе с хозяином в точке (XN, YN).
Ральф может бегать с любой скоростью, не превышающей в два раза скорость Боба. Пока Боб идет по прямой из точки в точку, собака ищет деревья, кусты, холмики и прочие интересные места, которые заданы парами целых чисел (X'j, Y'j). Всего таких мест M. Тем не менее, покидая своего хозяина в точке (Xi, Yi) (где 1 ≤ i ≤ N), Ральф посещает не более одного интересного места перед тем, как опять встретить хозяина в точке (Xi + 1, Yi + 1).
Ваша задача найти маршрут, удовлетворяющий указанным выше условиям, с максимальным количеством посещаемых интересных мест. Он представляется ломаной, по которой бегает Ральф. Ее вершинами должны быть все точки (Xi, Yi) и посещенные интересные места (X'j, Y'j). Последние должны быть посещены (то есть встречаться в описании пути) не более одного раза.
Пример пути Боба (сплошная линия), набора интересных мест (точки) и одного из лучших путей Ральфа представлены на рисунке:
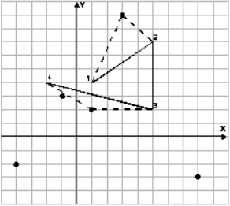
На первой строке через пробел записаны два числа N и M (2 ≤ N ≤ 100, 0 ≤ M ≤ 100). Вторая строка содержит N пар целых чисел X1, Y1, ..., XN, YN, разделенных пробелом, описывающих путь Боба. В третьей строке записано M пар целых чисел, (X'1, Y'1), ... (X'M, Y'M), разделенных пробелом, описывающих интересные места.
Все точки в условии различны и координаты по модулю не превосходят 1000.
В выходном файле должно быть единственное число K количество вершин в оптимальном маршруте Ральфа.
4 5 1 4 5 7 5 2 -2 4 -4 -2 3 9 1 2 -1 3 8 -3
6
Недавно королева страны AlgoLand придумала новый способ отмывания денег для своего королевского двора. Она решила, что всякий житель, желающий совершить путешествие из одного города страны в другой, должен расплатиться за это желание своими деньгами.
В стране AlgoLand есть N городов, пронумерованных от 1 до N. Некоторые города соединены дорогами, движение по которым разрешено в двух направлениях. Начиная движение по какой-нибудь дороге, путешественник обязательно должен доехать до ее конца.
Предположим теперь, что житель страны хочет совершить путешествие из города A в город B. Новый указ королевы гласит, что при проезде по любой дороге страны во время этого путешествия, полицейские могут взять с этого жителя таможенную пошлину в пользу королевского двора (а могут и не взять). Если при этом у жителя недостаточно денег для уплаты пошлины, то он автоматически попадает в тюрьму. Указ также устанавливает величину пошлины для каждой дороги страны. Так как королева заботится о жителях своей страны, то она запретила полицейским брать с жителя пошлину более чем два раза во время одного путешествия.
Отметим, что если существует несколько способов попасть из города A в город B, то житель может выбрать для путешествия любой из них по собственному желанию.
Напишите программу, которая определяет, какую минимальную сумму денег должен взять с собой житель, чтобы гарантированно не попасть в тюрьму во время путешествия.
Первая строка входного файла содержит числа N и M (2 ≤ N ≤ 10000, 1 ≤ M ≤ 100000), разделенные пробелом — количества городов и дорог. Следующие M строк описывают дороги. Каждая из этих строк описывает одну дорогу и содержит три числа X, Y, Z (1 ≤ X, Y ≤ N; X ≠ Y; 1 ≤ Z ≤ 100000000) разделенных пробелами, означающие, что дорога соединяет города X и Y и пошлина за ее проезд равна Z денежных единиц. Последняя строка содержит числа A и B (1 ≤ A, B ≤ N; A ≠ B) - номера начального и конечного городов путешествия. Гарантируется, что существует хотя бы один способ проезда из A в B.
Единственная строка выходного файла должна содержать одно число, равное минимальной сумме денег, которую должен взять с собой житель, чтобы иметь возможность совершить путешествие из города A в город B и при этом гарантированно не попасть в тюрьму независимо от действий полицейских.
5 6 1 5 1 5 4 1 5 2 2 4 2 1 3 2 1000000000 3 1 1000000000 1 3
1000000000
В одной из звездных систем Галактической Республики произошло дерзкое ограбление банка "13-е Общество межгалактического кредита", из которого было похищено несколько миллиардов буказоидов. Оказалось, что Армия Республики в данном секторе имеет ограниченные силы и не в состоянии блокировать все возможные пути бегства грабителей, поэтому встала задача о минимизации числа кордонов.
Звездные системы соединяются с помощью транспортных коридоров. Один армейский кордон может надежно блокировать только один транспортный коридор. Известно, что грабители еще не успели покинуть ограбленную звездную систему. Кроме этого известно множество систем, в которых грабители могут укрыться. Задача армии состоит в том, чтобы разместить минимальное количество кордонов таким образом, чтобы грабители не могли попасть ни в одну из этих систем.
Первым числорм в потоке входных данных задается общее число N всех звездных систем в галактике (2 ≤ N ≤ 1000). Мы будем предполагать, что все звездные системы пронумерованы от 1 до N. Система, в которой произошло ограбление, имеет номер 1. Далее вводится целое число H, обозначающее количество систем, в которых грабители могут укрыться. Затем перечисляются H целых чисел si (1 ≤ i ≤ H), задающее неповторяющиеся номера звездных систем (2 ≤ si ≤ N) укрытия. После этого вводится число T транспортных коридоров в галактике. Каждый транспортный коридор j (1 ≤ j ≤ T) задается парой целых чисел fj, tj (fj ≠ tj) – номеров звёздных систем, которые он соединяет. Транспортный коридор работает только в одном направлении от системы fj к системе tj. Любая пара звёздных систем может быть соединена максимум одним транспортным коридором. Транспортная сеть такова, что от системы 1 ко всем система sj существует путь, проходящий по транспортным коридорам.
Напечатайте сначала целое число M – минимальное количество необходимых кордонов. Затем напечатайте M транспортных коридоров, которые должны быть заблокированы. Каждый транспортный коридор должен быть выведен как пара целых чисел fk, tk.
5 1 5 6 1 2 1 3 2 3 2 4 3 4 4 5
1 4 5
До наступления летнего сезона ремонта теплотрасс по улицам города можно было проехать от любой площади до любой другой. При ремонте теплотрассы под какой-либо площадью движение по ней полностью перекрывается. Требуется определить, под какими из площадей ремонт теплотрассы нарушает возможность проезда из любого конца города, не затронутого ремонтом, в любой другой. Учесть, что в один и тот же момент времени ремонтная бригада работает только на одной из площадей.
В первой строке входного файла находятся числа N — количество площадей в городе и М — количество улиц их соединяющих (1 ≤ N ≤ 2000, 1 ≤ M ≤ 200000). Площади имеют номера от 1 до N. В каждой из следующих M строк находится пара натуральных чисел, описывающая между какими двумя площадями проходит соответствующая улица (две площади соединяются не более чем одной улицей).
На первой строке выведите число C — количество площадей, ремонт на которых недопустим. На следующей строке выведите C целых чисел — номера этих площадей в возрастающем порядке.
5 6 1 2 2 3 1 3 3 4 3 5 4 5
1 3
Задано подвешенное дерево, содержащее n (1 ≤ n ≤ 100000) вершин, пронумерованных от 0 до n - 1. Требуется ответить на m (1 ≤ m ≤ 100000) запросов о наименьшем общем предке для пары вершин.
Запросы генерируются следующим образом. Заданы числа a1, a2 и числа x, y и z. Числа a3, ..., a2m генерируются следующим образом: ai = (x·ai - 2 + y·ai - 1 + z)mod: n. Первый запрос имеет вид (a1, a2). Если ответ на (i - 1)-й запрос равен v, то i-й запрос имеет вид ((a2i - 1 + v)mod: n, a2i).
Первая строка содержит два числа: n и m. Корень дерева имеет номер 0. Вторая строка содержит n - 1 целых чисел, i-е из этих чисел равно номеру родителя вершины i. Третья строка содержит число содержит два целых числа в диапазоне от 0 до n - 1: a1 и a2. Четвертая строка содержит три целых числа: x, y и z, эти числа неотрицательны и не превосходят 109.
Выведите в выходной файл сумму номеров вершин — ответов на все запросы.
3 2 0 1 2 1 1 1 0
2