Обход в глубину(100 задач)
Способы задания графа(54 задач)
Минимальный каркас(12 задач)
Потоки(21 задач)
Паросочетания(17 задач)
Эйлеров цикл(9 задач)
Деревья(16 задач)
Охотник Боб часто гуляет со своей собакой Ральфом. Боб гуляет с постоянной скоростью и его путь – ломаная (возможно, самопересекающаяся), каждая вершина которой задается двумя целыми числами ( X i , Y i ) – декартовыми координатами.
Ральф бегает сам по себе, но обязательно должен встречаться с хозяином в указанных N точках. Собака начинает свой путь одновременно с хозяином в точке ( X 1 , Y 1 ) и завешает его вместе с хозяином в точке ( X N , Y N ) .
Ральф может бегать с любой скоростью, не превышающей в два раза скорость Боба. Пока Боб идет по прямой из точки в точку, собака ищет деревья, кусты, холмики и прочие интересные места, которые заданы парами целых чисел ( X ' j , Y ' j ) . Всего таких мест M. Тем не менее, покидая своего хозяина в точке ( X i , Y i ) (где 1 ≤ i ≤ N ), Ральф посещает не более одного интересного места перед тем, как опять встретить хозяина в точке ( X i + 1 , Y i + 1 ) .
Ваша задача – найти маршрут, удовлетворяющий указанным выше условиям, с максимальным количеством посещаемых интересных мест. Он представляется ломаной, по которой бегает Ральф. Ее вершинами должны быть все точки ( X i , Y i ) и посещенные интересные места ( X ' j , Y ' j ) . Последние должны быть посещены (то есть встречаться в описании пути) не более одного раза.
Пример пути Боба (сплошная линия), набора интересных мест (точки) и одного из лучших путей Ральфа представлены на рисунке:
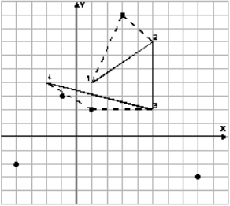
На первой строке через пробел записаны два числа N и M (2 ≤ N ≤ 100, 0 ≤ M ≤ 100) . Вторая строка содержит N пар целых чисел X 1 , Y 1 , ..., X N , Y N , разделенных пробелом, описывающих путь Боба. В третьей строке записано M пар целых чисел, ( X ' 1 , Y ' 1 ) , ... ( X ' M , Y ' M ) , разделенных пробелом, описывающих интересные места.
Все точки в условии различны и координаты по модулю не превосходят 1000 .
В выходном файле должно быть единственное число K – количество вершин в оптимальном маршруте Ральфа.
4 5 1 4 5 7 5 2 -2 4 -4 -2 3 9 1 2 -1 3 8 -3
6
Гора состоит из площадок, соединенных между собой узкими проходами. На каждой площадке лежит какое-то количество камней. У разных площадок разный рейтинг, зависящий от высоты площадки — чем выше площадка, тем больше ее рейтинг среди камней. Очевидно, что на площадках с более высоким рейтингом лежит большее количество камней.
В один солнечный день главный камень одной из площадок обратил внимание, что вокруг стало очень тесно. Но камни не могут катиться вверх, а на нижние площадки они катиться не хотят из-за плохого рейтинга. Поэтому главный камень пошел на хитрость. Он выбрал M камней и сказал каждому из них, что где-то внизу появилась замечательная площадка с самым высоким рейтингом на горе. Для полной правдоподобности он составил карту площадок, на которые можно скатиться с его площадки. Всего (включая переполненную площадку) оказалось N площадок. Поскольку главный камень ленивый, он не стал рисовать все пути между площадками, а просто нарисовал минимальное количество проходов между площадками, чтобы из его площадки можно было добраться в любую, находящуюся ниже. Он показал каждому из M камней эту карту и объяснил, где находится замечательная площадка (чтобы камень запомнил путь). Причем, чтобы главные камни нижних площадок не имели к нему претензий из-за такого нашествия, некоторым камням он показал на другие площадки, чем остальным. Чтобы не создать лавину, он сказал камням катиться с небольшим интервалом между собой. Немного подумав, он решил, что можно пускать камни парами, чтобы пространство быстрее освободилось. Камни ему поверили и стали собираться в дорогу.
Камни не любят скучать, поэтому каждая пара решила посчитать, сколько времени они будут катиться вместе, и, может быть, перестроить пары, чтобы увеличить это время. На то, чтобы скатиться по проходу с одной площадки в следующую, не заходя по пути на другие площадки, камень тратит одну минуту. Но складывать числа камни не умеют, в этом им требуется ваша помощь.
В первой строке входного файла записаны два целых числа - N и K , где 1 ≤ N ≤25000, K = M / 2, 0 ≤ M ≤ 2000 . В следующих ( N –1) строках находятся пары чисел i и j , означающие, что из i -й площадки можно напрямую скатиться на j -ю. Площадки занумерованы числами от 1 до N , верхняя площадка, откуда катятся камни, может иметь любой номер. Записанных пар номеров площадок достаточно, чтобы определить путь из самой верхней площадки до любой другой. Дальше идут K строк, на каждой строке через пробел записана пара чисел a и b (1 ≤ a , b ≤ N ) , обозначающая пункты назначения для очередной пары камней: первый камень катится на площадку a , а второй — на площадку b .
В выходной файл нужно вывести K строк, на каждой строке должно находиться по три целых числа a , b и c , записанных через пробел. Эти числа означают, что пара камней, направляющихся на площадки a и b , будет катиться вместе c минут. Тройки чисел нужно выдавать в том же порядке, в котором перечислены соответствующие им пары во входном файле.
6 2 1 2 1 3 1 4 3 5 3 6 2 4 5 6
2 4 0 5 6 1
Гора состоит из площадок, соединенных между собой узкими проходами. На каждой площадке лежит какое-то количество камней. У разных площадок разный рейтинг, зависящий от высоты площадки — чем выше площадка, тем больше ее рейтинг среди камней. Очевидно, что на площадках с более высоким рейтингом лежит большее количество камней.
В один солнечный день главный камень одной из площадок обратил внимание, что вокруг стало очень тесно. Но камни не могут катиться вверх, а на нижние площадки они катиться не хотят из-за плохого рейтинга. Поэтому главный камень пошел на хитрость. Он выбрал M камней и сказал каждому из них, что где-то внизу появилась замечательная площадка с самым высоким рейтингом на горе. Для полной правдоподобности он составил карту площадок, на которые можно скатиться с его площадки. Всего (включая переполненную площадку) оказалось N площадок. Поскольку главный камень ленивый, он не стал рисовать все пути между площадками, а просто нарисовал минимальное количество проходов между площадками, чтобы из его площадки можно было добраться в любую, находящуюся ниже. Он показал каждому из M камней эту карту и объяснил, где находится замечательная площадка (чтобы камень запомнил путь). Причем, чтобы главные камни нижних площадок не имели к нему претензий из-за такого нашествия, некоторым камням он показал на другие площадки, чем остальным. Чтобы не создать лавину, он сказал камням катиться с небольшим интервалом между собой. Немного подумав, он решил, что можно пускать камни парами, чтобы пространство быстрее освободилось. Камни ему поверили и стали собираться в дорогу.
Камни не любят скучать, поэтому каждая пара решила посчитать, сколько времени они будут катиться вместе, и, может быть, перестроить пары, чтобы увеличить это время. На то, чтобы скатиться по проходу с одной площадки в следующую, не заходя по пути на другие площадки, камень тратит одну минуту. Но складывать числа камни не умеют, в этом им требуется ваша помощь.
В первой строке входного файла записаны два целых числа — N и K , где 1 ≤ N ≤ 500000 , K = M / 2 , 0 ≤ M ≤ 1000000 . В следующих ( N –1) строках находятся пары чисел i и j , означающие, что из i -й площадки можно напрямую скатиться на j -ю. Площадки занумерованы числами от 1 до N , верхняя площадка, откуда катятся камни, может иметь любой номер. Записанных пар номеров площадок достаточно, чтобы определить путь из самой верхней площадки до любой другой. Дальше идут K строк, на каждой строке через пробел записана пара чисел a и b (1 ≤ a , b ≤ N ) , обозначающая пункты назначения для очередной пары камней: первый камень катится на площадку a , а второй — на площадку b .
В выходной файл нужно вывести K строк, на каждой строке должно находиться по три целых числа a , b и c , записанных через пробел. Эти числа означают, что пара камней, направляющихся на площадки a и b , будет катиться вместе c минут. Тройки чисел нужно выдавать в том же порядке, в котором перечислены соответствующие им пары во входном файле.
1 ≤ N ≤ 25 000, 1 ≤ M ≤ 2 000. Решение оценивается в 55 баллов.
Дополнительные ограничения отсутствуют. Решение оценивается в 45 баллов.
6 2 1 2 1 3 1 4 3 5 3 6 2 4 5 6
2 4 0 5 6 1
В маленьком городке М начала действовать служба контроля за незаконными полетами НЛО. Первая задача службы — выяснить, сколько НЛО действует в окрестности города. Агенты службы опросили множество свидетелей и составили список случаев встречи с НЛО, произошедших за одни сутки, с указанием места и времени наблюдения. Теперь аналитики хотят понять, сколько же на самом деле было НЛО. Из данных разведки известна максимальная скорость, с которой может лететь НЛО. Аналитики просят вас узнать, какое минимальное количество НЛО могли наблюдать свидетели.
На первой строке входного файла содержатся целые числа n и v — количество случаев наблюдения и максимальная скорость НЛО ( 1 ≤ n ≤ 100 , 1 ≤ v ≤ 10000 ). Следующие n строк содержат описания случаев встречи с НЛО в формате «ЧЧ:ММ x y», где ЧЧ:ММ — время встречи, x и y — координаты места, в котором наблюдался НЛО (для простоты будем считать, что все встречи происходили на плоскости). Координаты по модулю не превышают 1000 . Скорость выражена в км/ч, координаты — в км.
Выведите в выходной файл одно число — минимальное возможное количество НЛО.
4 1 12:00 0 0 13:10 0 1 14:00 1 0 15:00 1 1
2
На одной из планет, под названием TheBestWorld, живут много умных людей. Эта планета также известна своими двумя конкурирующими школами супергероев. Каждый малыш, живущий на этой планете, мечтает стать супергероем, но не у всех это получается.
Ученики разных школ всегда недолюбливали друг друга. И иногда дело даже доходило до того, как супергерои начали применять свои геройские силы для выяснения отношений.
В этом мире случилось несчастье. На TheBestWorld нападают темные силы. У генерала главнокомандующего армией супергероев есть в распоряжении n + m супергероев, из них n — выпускники первой школы, m — второй. Главнокомандующий подсчитал количество супергероев k , которые смогут спасти лучшее, что у них есть, — планету.
На первый взгляд кажется, что главнокомандующему не понадобится помощь в выборе супергероев, но он вспомнил, что супергерои из разных школ раздражают друг друга. Но это происходит только тогда, когда два супергероя из разных школ находятся на расстоянии меньше d . Если такую пару героев позвать спасать мир, они не смогут продуктивно делать свою работу.
Проблема в том, что генерал забыл искомое d . Вам известны координаты каждого из супергероев. Генерал просит вас вычислить максимальное d , при котором он все еще может спасти мир. И выдать список супергероев, которые спасут мир при данном d .
В первой строке входного файла заданы три числа n , m и k ( 1 ≤ k , n , m ≤ n + m ≤ 200 ) — количество супергероев, выпустившихся из первой и второй школы, и количество супергероев, которое необходимо, чтобы спасти мир, соответственно. Следующие n + m строк описывают супергероев: в каждой строке заданы два целых числа — текущие координаты супергероя. Первые n строк содержат информацию о выпускниках первой школы, следующие m — о выпускниках второй школы. Все координаты не превышает по модулю 10000 . Известно, что никакие два супергероя не стоят в одной точке.
В первую строку выходного файла выведите одно вещественное число: максимальное значение d , которое позволяет спасти мир, либо -1, если при любом значении d мир можно спасти. Относительная или абсолютная погрешность вашего ответа не должна превышать 10 −6 . В следующих k строках выведите список номеров супергероев по одному числу в строке, которых можно взять при данном d , либо, если спасти мир можно при любом d , выведите список героев, которые позволяет спасти мир вне зависимости от d . Супергерои нумеруются числами от 1 до n + m в том порядке, в котором они идут во входном файле.
2 3 4 1 1 1 2 1 3 1 4 1 5
2.000000000000000000 1 3 4 5
1 1 2 1 1 1 10
9.000000000000000000 1 2