#112817

Вышивка жемчугом

Темы: [Сканирующая прямая] [Алгоритмы на графах]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Заключительный этап, 2015, 1 тур, Задача C ]

Дано изображение дерева из $n$ вершин на прямоугольной сетке. Каждое ребро — либо вертикальный, либо горизонтальный отрезок длины $1$ Дано $q$ запросов, каждый имеет вид "сколько компонент связности образуется при вырезании данного прямоугольного фрагмента"

Со стародавних времён в поморских деревнях рукодельницы вышивали жемчугом на прямоугольных полотенцах, состоящих из одинаковых клеток. Вышивка начиналась с пришивания жемчужины к полотенцу в центре одной из клеток. Чтобы пришить новую жемчужину, рукодельница делала стежок из клетки, уже содержащей жемчужину, в соседнюю с ней по горизонтали или вертикали свободную клетку. Новая жемчужина пришивалась в центре клетки на конце стежка. Этот процесс повторялся, пока не заканчивались жемчужины.

Одно из таких праздничных полотенец находится в музее. К сожалению, некоторые части узора были утеряны, но описание полотенца сохранилось. Дирекция музея планирует восстановить один из прямоугольных фрагментов полотенца, но не ещё не решила какой именно. Затраты на восстановление фрагмента зависят от количества связных частей узора, попавших на этот фрагмент. Часть узора считается связной, если от любой её жемчужины можно по стежкам перейти к любой другой её жемчужине, не выходя за границы фрагмента. Дирекция всегда относит любые две жемчужины, между которыми можно перейти по стежкам, к одной и той же связной части узора.

Требуется написать программу, вычисляющую количество связных частей узора для каждого из заданных фрагментов.

Входные данные

Первая строка входных данных содержит два целых числа a и b — размеры полотенца в клетках по горизонтали и вертикали.

Вторая строка содержит два числа $n$ и $q$ — количество жемчужин в узоре и количество фрагментов соответственно.

Следующие ($n − 1$) строк содержат описания стежков. Каждый стежок имеет один из следующих видов:

• $h \times y$ означает, что клетки с координатами $(x, y)$ и $(x + 1, y)$ содержат жемчужины, соединённые горизонтальным стежком ($1 \le x \le a − 1; 1 \le y \le b$);

• $v \times y$ означает, что клетки с координатами $(x, y)$ и $(x, y + 1)$ содержат жемчужины, соединённые вертикальным стежком ($1 \le x \le a; 1 \le y \le b − 1$).

Так как неизвестно в каком порядке рукодельница наносила стежки, их описания следуют в произвольном порядке. При этом гарантируется, что узор был получен в результате процесса, описанного в условии задачи.

Следующие $q$ строк описывают фрагменты. Каждое описание содержит четыре целых числа $x_1$, $y_1$, $x_2$ и $y_2$ — координаты левой нижней и правой верхней клетки фрагмента ($1 \le x_1 \le x_2 \le a; 1 \le y_1 \le y_2 \le b$).

Выходные данные

Выходные данные должны содержать $q$ строк, где $i$-я строка содержит количество связных частей узора в $i$-м фрагменте.

Таблица системы оценивания

Замечание

Пояснение к тесту из условия

Примеры

Входные данные

Выходные данные

#112902

Transformation Sequence

Темы: [Паросочетания]

Для каждой пары чисел $x$ и $y$ из диапазона $0,1,2,\ldots,N-1$ определим расстояние $D(x,y)$ как $min(|x-y|,N-|x-y|)$. Для перестановки $T$ можно построить набор чисел $D_i=D(i,T_i)$. Ваша задача состоит в обратном: по заданному набору чисел восстановить корректную перестановку, а среди таких требуется выбрать лексикографически минимальную.

Формат входных данных

В первой строке входных данных содержится число $N$ - размер перестановки. В следующей строке содержатся числа $D_0,D_1,\ldots,D_{N-1}$.

Формат выходных данных

В случае, если такой перестановки не существует, выведите «No Answer». В противном случае выведите искомую оптимальную перестановку.

Система оценки

В 30% тестовых примеров выполнено $N \le 50$
В 60% тестовых примеров выполнено $N \le 500$
В 100% тестовых примеров выполнено $N \le 10\,000$

#112922

Алканы

Темы: [Обход в глубину]

Алканы (также насыщенные углеводороды, парафины, алифатические соединения) — ациклические углеводороды линейного или разветвленного строения, содержащие только простые связи. Алканы являются насыщенными углеводородами и содержат максимально возможное число атомов водорода. Каждый атом углерода в молекулах алканов находится в состоянии sp³-гибридизации — все четыре гибридные орбитали атома С идентичны по форме и энергии, четыре связи направлены в вершины тетраэдра под углами $\text{[math]}$ . Cвязи C–C представляют собой σ-связи, отличающиеся низкой полярностью и поляризуемостью.

Ничего не поняв, вы обратились к однокласснику за помощью. Он сказал вам забыть всё, что было написано в учебнике, и объяснил, что алканы — углеводороды. То есть соединения, состоящие из атомов углерода и водорода, не содержащие связей водород–водород, причём каждый углерод соединен ровно с четырьмя другими атомами, а каждый водород соединен ровно с одним другим атомом. При этом алкан является связным соединением, а также молекула алкана не является цикличной (для каждых двух атомов существует единственный способ добраться из одного в другой по связям между атомами). Также он сказал, что связи между атомами всегда соединяют два различных атома.

Запомнив всё это, вы пошли к Александру Евгеньевичу, и он дал вам задание: для данного соединения определить, является ли оно алканом.

Входные данные

В первой строке содержатся два числа N и M (1 ≤ N ≤ 100 000, 0 ≤ M ≤ 100 000) — количество атомов и соединений между атомами соответственно.

Следующая строка состоит из N символов. Если i-й символ — «C», то i-й атом — атом углерода. Если i-й символ — «H», то i-й атом — атом водорода. Гарантируется, что каждой символ этой строки — либо «C», либо «H».

В следующих M строках содержатся описания соединений между атомами. В i-й из них содержатся номера двух атомов, связанных i-м соединением.

Выходные данные

Выведите «YES», если соединение является алканом, и «NO», если не является.

Примеры тестов

Входные данные

Выходные данные

YES

Входные данные

2 1
CH
1 2

Выходные данные

NO

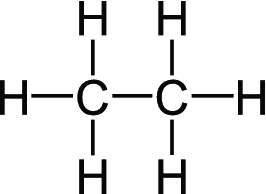
Соединение в первом примере является молекулой этана. Ниже представлена его структурная формула.

$\text{[math]}$

#113441

Размещение данных

Темы: [Мосты] [Алгоритмы на графах] [Обход в глубину]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Региональный этап, 2017, 1 день, Задача C ]

Телекоммуникационная сеть крупной IT-компании содержит n серверов, пронумерованных от 1 до $n$. Некоторые пары серверов соединены двусторонними каналами связи, всего в сети m каналов. Гарантируется, что сеть серверов устроена таким образом, что по каналам связи можно передавать данные с любого сервера на любой другой сервер, возможно с использованием одного или нескольких промежуточных серверов.

Множество серверов $A$ называется отказоустойчивым, если при недоступности любого канала связи выполнено следующее условие. Для любого не входящего в это множество сервера $X$ существует способ передать данные по остальным каналам на сервер $X$ хотя бы от одного сервера из множества $A$.

На рис. 1 показан пример сети и отказоустойчивого множества из серверов с номерами 1 и 4. Данные на сервер 2 можно передать следующим образом. При недоступности канала между серверами 1 и 2 — с сервера 4, при недоступности канала между серверами 2 и 3 — с сервера 1. На серверы 3 и 5 при недоступности любого канала связи можно по другим каналам передать данные с сервера 4.

В рамках проекта группе разработчиков компании необходимо разместить свои данные в сети. Для повышения доступности данных и устойчивости к авариям разработчики хотят продублировать свои данные, разместив их одновременно на нескольких серверах, образующих отказоустойчивое множество. Чтобы минимизировать издержки, необходимо выбрать минимальное по количеству серверов отказоустойчивое множество. Кроме того, чтобы узнать, насколько гибко устроена сеть, необходимо подсчитать количество способов выбора такого множества, и поскольку это количество способов может быть большим, необходимо найти остаток от деления этого количества способов на число $10^9 + 7$.

Требуется написать программу, которая по заданному описанию сети определяет следующие числа: $k$ — минимальное количество серверов в отказоустойчивом множестве серверов, $c$ — остаток от деления количества способов выбора отказоустойчивого множества из $k$ серверов на число $10^9 + 7$

Входные данные

Первая строка входного файла содержит целые числа $n$ и $m$ — количество серверов и количество каналов связи соответственно ($2 \le n \le 200000$, $1 \le m \le 200000$). Следующие $m$ строк содержат по два целых числа и описывают каналы связи между серверами. Каждый канал связи задается двумя целыми числами: номерами серверов, которые он соединяет.

Гарантируется, что любые два сервера соединены напрямую не более чем одним каналом связи, никакой канал не соединяет сервер сам с собой, и для любой пары серверов существует способ передачи данных с одного из них на другой, возможно с использованием одного или нескольких промежуточных серверов.

Выходные данные

Выведите два целых числа, разделенных пробелом: $k$ — минимальное число серверов в отказоустойчивом множестве серверов, $c$ — количество способов выбора отказоустойчивого множества из $k$ серверов, взятое по модулю $10^9 + 7$

Пояснения к примеру

В приведенном примере отказоустойчивыми являются следующие множества из двух серверов: {1, 3}, {1, 4}, {1, 5}.

Описание подзадач и системы оценивания

Баллы за каждую подзадачу начисляются только, если все тесты для этой подзадачи и всех необходимых подзадач успешно пройдены.

Примеры

Входные данные

Выходные данные

2 3

#113466

Центроиды дерева

Темы: [Центроиды]

Дано дерево из n вершин. У каждой вершины есть цвет. Нужно обработать q запросов ( v _i , c _i ): найти расстояние от v _i до ближайшей к v _i вершины цвета c _i . Расстоянием между вершинами называется минимальное количество рёбер в пути между ними.

Входные данные

На первой строке число n ( 1 ≤ n ≤ 10 ⁵ ), следующая строка содержит числа p ₁ , p ₂ , ..., p _{n

- 1} . 0 ≤ p _i < i . p _i – отец вершины i в дереве. Далее строка с числами a ₀ , a ₁ , ..., a _{n

- 1} . 0 ≤ a _i < n . a _i – цвет вершины i . Далее строка с числом q ( 1 ≤ q ≤ 10 ⁵ ). Следующие q строк содержат запросы v _iq _i ( 0 ≤ v _i < n , 0 ≤ c _i < n ).

Выходные данные

Для каждого запроса выведите одно число – расстояние до ближайшей вершины нужного цвета, или - 1 , если в дереве нет вершин такого цвета.

Решения, работающие при $1 \leq n \leq 200$, будут набирать не менее 30 баллов

Примеры

Входные данные

Выходные данные

0 1 2 -1 2 1 2 1 1