Страница: << 58 59 60 61 62 63 64 >> Отображать по:

#114092

Необычная яблоня

Темы: [Обход в глубину] [Деревья]

У Аркадия в саду есть одна необычная яблоня, с которой иногда необходимо собирать яблоки. Так как яблоня необычная, на ней есть $n$ соцветий, они пронумерованы от 1 до $n$. Соцветие номер 1 находится около корня дерева, любое другое соцветие с номером $i(i>1)$ расположено на верхнем конце ветки, нижний конец которой расположен в соцветии $p_i$.

Когда яблоки созревают, одновременно появляется ровно по одному яблоку в каждом соцветии. В тот же момент все яблоки начинают скатываться вниз по веткам к корню дерева. Каждую секунду все яблоки, кроме находящегося в первом соцветии, одновременно скатываются на одну ветку ближе к корню, то есть, например, из соцветия a яблоко попадет в соцветие $p_a$. Яблоки, находившиеся в первом соцветии, забирает Аркадий. Яблоня необычная, поэтому, если в какой-то момент в одном соцветии оказываются два яблока, они аннигилируют. Так происходит с каждой парой, например, если в соцветие попадет одновременно 5 яблок, то останется только одно яблоко, а если в соцветие попадет одновременно 8 яблок, то не останется ни одного яблока. Таким образом, в каждом соцветии в любой момент времени находится не более одного яблока.

Помогите Аркадию, подсчитайте, сколько яблок он сможет забрать из первого соцветия за один урожай.

Входные данные

В первой строке следует целое число $n(2 \le n \le 100000)$ — количество соцветий.

Во второй строке следует последовательность целых чисел $p_2, p_3, ..., p_n$, состоящая из $n−1$ числа, где $p_i$ равно номеру соцветия, в которое скатывается яблоко из соцветия $i$.

Выходные данные

Выведите количество яблок, которые Аркадий сможет забрать из первого соцветия за один урожай.

Примеры

Входные данные

3
1 2

Выходные данные

Входные данные

5
4 2 5 1

Выходные данные

#114305

Телепортация_0

Темы: [Алгоритмы на графах] [Обход в ширину]

На дворе $3020$ год. Король Байтазар правит огромной планетарной системой, в которой насчитывается целых $n$ планет. В $3020$ году люди отказались от традиции давать планетам имена и вместо этого используют номера. Дворец Байтазара находится на планете под номером $1$, в то время как его военная база находится на планете под номером $2$. Давным давно для Байтазара был построен портал, соединяющий планеты $1$ и $2$, который позволяет добираться с планеты номер $1$ на планету номер $2$ или обратно за $250$ минут (немногим больше четырёх часов).

С тех пор технологии шагнули далеко вперёд, и современные порталы позволяют добиратся между планетам всего за $1$ час (в $3020$ году в часе всё ещё $60$ минут). Порталы, разумеется, остались двухсторонними. Некоторые из планет уже соединены современными версиями порталов (но не планеты $1$ и $2$ - король Байтазар крайне консервативен). Вообще, уже сейчас возможно добраться от планеты $1$ до планеты $2$ используя имеющиеся новые порталы, но личный портал Байтазара остаётся самым быстрым способом добраться между планетами $1$ и $2$.

Технология быстрой телепортации продолжает своё распространение и Байтазар хочет это поддержать, не желая между тем менять свой личный портал старого типа на новый. При этом, из соображений безопасности Байтазар не хочет, чтобы был способ добраться с планеты $1$ на планету $2$ быстрее, чем его личный портал. Помогите Байтазару. Найдите максимальное число новых порталов, которые можно построить так, чтобы личный портал Байтазара оставался самым быстрым путем перемещения между резиденцией и военной базой.

Входные данные

В первой строке даны два числа $n$ и $m$ ($ 2 \le n \le 40000, 1 \le m \le 1000000$) - количество планет в планетарной системе Байтазара и количество двусторонних порталов нового типа соответственно.

В последующих $m$ строках дано описания порталов. Каждая строка содержит два целых числа $v$ и $u$, ($1 \le v, u \le n$, $v \ne u$), что означает что планеты $v$ и $u$ соединены порталом нового типа.

Гарантируется, что существует способ добраться с планеты $1$ на планету $2$ используя имеющиеся порталы и что такое путешествие займёт строго больше $250$ минут.

Выходные данные

Выведете единственное число $ans$ - наибольшее количество порталов которое можно построить в планетарной системы Байтазара, так чтобы личный портал Байтазара оставался самым быстрым путем перемещения между резиденцией и военной базой.

Система оценки

В тестах суммарной стоимостью не менее $20$ баллов дополнительно гарантируется что $n \le 8$, $m \le 9$.

В тестах суммарной стоимостью не менее $30$ баллов дополнительно гарантируется что $n \le 12$, $m \le 20$.

В тестах суммарной стоимостью не менее $60$ баллов дополнительно гарантируется что $n \le 150$, $m \le 4000$.

Примечание

Иллюстрация к первому примеру:

$\text{[math]}$

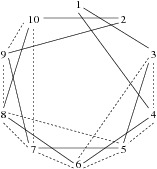
Жирными линиями показаны имеющиеся скоростные порталы, в то время как пунктирными линиями показаны те порталы, которые Байтазар может построить, не подвергнув государство опасности и построив при этом максимально возможное количество скоростных порталов.

Примеры

Входные данные

Выходные данные

#114307

Клуб

Темы: [Паросочетания] [Применение обхода в глубину] [Эйлеров цикл]

Бойцовский клуб дебатов - необычный клуб во всех отношениях. Каждый из $2^{n}$ его членов заполнил специальную анкету, содержащую $n$ вопросов с бинарным ответом (да/нет) о своих взглядах. Ответы каждого человека могут быть представлены в виде последовательности из $n$ бит, иначе говоря в виде числа от $0$ до $2^{n} - 1$.

Перечислим ещё несколько инетерсных фактов о бойцовском клубе дебатов.

взгляды никаких двух членов клуба не совпадают, т. е. каждое из чисел от от $0$ до $2^{n} - 1$ встречается в числовых представлениях анкеты клуба
ровно половина членов клуба мужчины, остальные - женщины (т. е. и мужчин, и женщин по $2^{n - 1}$) и они формируют $2^{n - 1}$ разнополых пар
два члена клуба считаются близкими по взглядам тогда, и только тогда когда у них в анкете отличается ответы ровно на один вопрос (иначе говоря, $a_i \oplus b_i = 2^k$ для некоторого $k$, где $a_i$ и $b_i$ - числа, кодирующие взгляды первого и второго человека соответственно)
во время дебатов члены клуба сидят за круглым столом
члены клуба хотят сидеть так, чтобы соеседями с одной стороны была его пара, с другой стороны, человек, близкий ему по взглядам

Входные данные

В первой строке вводится число $n$ ($2 \le n \le 18$) - количество вопросов в анкете.

В последующих $2^{n - 1}$ строках даны пары людей. В $i$ строке даны целые числа $a_i$ и $b_i$, разделённые одним пробелом - что означает, что люди, чьи анкеты закодированы числами $a_i$ и $b_i$ являются парой. Гарантируется, что каждое целое число от $0$ до $2^{n} - 1$ встретится во вводе ровно один раз.

Выходные данные

Выведете строку со единственным словом 'NO' , если не существует рассадки членов клуба по местам удоволетворяющей условию.

Иначе, выведете в первой строке слово 'YES'. Во второй строке выведите $2 ^ n$ чисел, разделённые пробелами, кодирующие ответы последовательных людей вокруг стола - корректную рассадку (стол круглый, поэтому можно начинать вывод с любого человека).

Если существует несколько решений, выведите любое.

Система оценки

В задаче оценка по подгруппам. Подгруппы отличаются значением $n$. Для для $n = 2$ - $4$ балла за подгруппу, для каждого значения $n$ от $3$ до $18$ по $6$ баллов за подгруппу.

Примеры

Входные данные

Выходные данные

YES
0 5 7 2 6 3 1 4

#114309

Убежище

Темы: [Паросочетания] [Лемма Холла] [Динамика по подмножествам]

В полутемной комнате Милан сел за стол и начал думать о возможных последствиях ядерной катастрофы в своем городе. Поскольку Милан - мэр города, он очень хорошо знаком с такими событиями.

А именно, он знает, что в его городе живет ровно $N$ человек и каждый житель живет в своем собственном доме. Между $M$ парами домов есть дороги, и для каждой дороги известно, сколько времени потребуется для ее прохождения. Наконец, Милан знает, в каких $K$ домах есть атомные укрытия и сколько людей помещается в каждое укрытие. Учитывая все это, у Милана возникает следующий вопрос: «Сколько времени нужно, чтобы эвакуировать всех жителей города?»

Помогите Милану ответить на этот вопрос.

Конечно, эвакуация означает, что каждый житель попадает в какое-то атомное убежище. Можно предположить, что жители двигаются оптимально (по кратчайшему пути) и что несколько человек могут двигаться по одной дороге одновременно, возможно в разных направлениях. Также можно считать, что между любыми двумя домами есть хотя бы один путь, проходящий по дорогам.

Входные данные

Первая строка содержит натуральные числа N $(1 \le N \le 100000)$, $M$ $(1 \le M \le 300000)$ и $K$ $(1 \le K \le 17)$, которые обозначают количество жителей, количество дорог и количество атомных укрытий. Дома пронумерованы числами от $1$ до $N$.

В каждой из следующих $M$ строк даны три натуральных числа $A$, $B$ $(1 \le A, B \le N, A \neq B)$ и $C$ $(1 \le C \le 10^9)$, которые обозначают, что между домами с номерами $A$ и $B$ есть дорога, для прохождения которой требуется $C$ единиц времени.

В каждой из следующих $K$ строк даны два натуральных числа $X$ $(1 \le X \le N)$ и $Y$ $(1 \le Y \le 10^9)$, которые обозначают, что в доме с номером $X$ есть атомное убежище, где может быть укрыто максимум $Y$ людей.

Общая вместимость всех укрытий больше или равна $N$.

Выходные данные

В единственной строке выведите минимальное время, необходимое для эвакуации всех жителей города.

Система оценки

В задаче 3 подгруппы:

(30 баллов) Ограничения: $N \le 100, M \le 500, K \le 5$
(30 баллов) Ограничения: $K \le 10$
(40 баллов) Без дополнительных ограничений.

Примеры

Входные данные

Выходные данные

Входные данные

Выходные данные

#114311

Везувий

Темы: [Бор] [Топологическая сортировка]

Члены комиссии соревнования ICPC не смогли придумать задачи, поэтому они решили ранжировать команды лексикографически. Таким образом, победителем станет команда, название которой лексикографически самое маленькое. Героиня этой задачи, Этна, является лидером команды, личность которой мы будем скрывать. Название её команды начинается с буквы «Z», что ставит её в довольно плохое положение. После долгих разговоров с комитетом Этна смогла добиться более справедливого способа ранжирования команд. К сожалению, команды будут продолжать сортировать лексикографически, но определение лексикографического порядка изменится. А именно, комитет случайным образом выберет перестановку букв английского алфавита и определит лексикографический порядок, используя эту перестановку. Этна сразу же достала свой ноутбук и написала программу, которая находит перестановку букв для каждой команды, согласно которой эта команда выиграет соревнование. К сожалению, программа еще не закончена. Помогите Этне и напишите более эффективную программу с той же функциональностью.

Входные данные

На первной строке дано натуральное число $N$, которое обозначает количество команд, участвующих в соревновании.

В следующих $N$ строках даны названия команд, участвующих в соревновании. Название каждой команды состоит из одного слова, которое в свою очередь состоит из строчных букв английского алфавита. Конечно, названия команд отличаются друг от друга.

Выходные данные

Для каждой команды в исходном порядке необходимо вывести перестановку букв английского алфавита, в соответствии с которой эта команда выиграет соревнование. Если такой перестановки нет, необходимо вывести слово «nemoguce», а если таких перестановок несколько, достаточно вывести любую.

Система оценки

В этой задаче 3 подгруппы. Обозначим $L$ - суммарную длину строк, $K$ - количество различных букв.

(13 баллов) $1 \le N \le 100, 1 \le L \le 10000, 1 \le K \le 6$

(32 балла) $1 \le N \le 350, 1 \le L \le 10000, 1 \le K \le 26$

(55 баллов) $1 \le N \le 25000, 1 \le L \le 1000000, 1 \le K \le 26$

Примеры

Входные данные

3
war
zag
wro

Выходные данные

yxwzvutsqponmlkjihgfedcbar
zyxwvutsrqponmlkjihgfedcba
yxwzvutsrqponmlkjihgfedcba

Входные данные

3
b
ab
aa

Выходные данные

zyxwvutsrqponmlkjihgfedcba
nemoguce
zyxwvutsrqponmlkjihgfedcab

Входные данные

7
bcada
dbaab
bbabc
ababb
aacdf
bcdff
baddb

Выходные данные

zyxwvutsrqponmlkjihgfecbad
zyxwvutsrqponmlkjihgfedcba
zyxwvutsrqponmlkjihgfebdca
nemoguce
zyxwvutsrqponmlkjihgfecadb
zyxwvutsrqponmlkjihgfecbda
nemoguce

Страница: << 58 59 60 61 62 63 64 >> Отображать по:

Выбрано

Отменить

Добавить в контест