Темы --> Информатика --> Алгоритмы --> Алгоритмы поиска
    Линейный поиск(29 задач)
    Бинарный поиск(101 задач)
    Порядковые статистики(3 задач)
    Поиск подстроки в строке(1 задач)
    Тернарный поиск(8 задач)
    "Два указателя"(18 задач)
---> 155 задач <---
Источники
    Личные олимпиады(938 задач)
    Командные олимпиады(684 задач)
Страница: << 25 26 27 28 29 30 31 Отображать по:
#113937
Гномы, шляпы и экстрасенсорные способности
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes

Это интерактивная задача.

В былые времена гномы пытались развить у себя экстрасенсорные способности:

  • В абсолютно тёмную пещеру заводили n гномов.
  • На каждого гнома надевали шляпу — белую или чёрную. Гномы в пещере не видели цветов своих шляп и шляп других гномов.
  • Гномы по очереди выходили из пещеры на поляну и садились на произвольное места. При этом, выходя из пещеры, каждый гном видел цвета шляп всех гномов, вышедших ранее. Тем не менее, он не видит цвет собственной шляпы и никто из других гномов ему этот цвет не сообщает.
  • Задача состояла в том, чтобы все гномы разошлись в две стороны — в одну те, кто носят белые шляпы и в другую — чёрные.

За многие века гномы научились безошибочно выбирать для себя место на поляне. Получится ли подобное у вас?

Вас просят по очереди назвать n различных точек на плоскости с целочисленными координатами. После указания очередной точки вам будет сообщён её цвет — чёрный или белый. Ваша задача — добиться того, чтобы названные точки можно было разбить прямой так, чтобы точки одного цвета лежали по одну сторону от прямой, точки разного цвета — по разные стороны и никакие точки не лежали на прямой. Также вы должны предъявить такую прямую.

В данной задаче интерактор является адаптивным — цвета точек в тесте заранее не зафиксированы и программа жюри может выбирать их произвольным образом, в том числе учитывая вывод вашей программы.

Протокол взаимодействия

В первой строке стандартного потока ввода дано целое число n ( 1 ≤ n ≤ 30 ) — количество точек, которое должна назвать ваша программа.

Затем n раз ваша программа должна вывести по два целых числа x и y ( 0 ≤ x ≤ 10 9 , 0 ≤ y ≤ 10 9 ) — координаты очередной точки. Все выведенные вами точки должны быть различными.

В ответ на каждую пару координат ваша программа получит на вход строку « black », если точка имеет чёрный цвет, или « white », если точка имеет белый цвет.

После того, как все n точек будут обработаны, вы должны вывести четыре целых числа x 1 , y 1 , x 2 и y 2 ( 0 ≤ x 1 , y 1 ≤ 10 9 , 0 ≤ x 2 , y 2 ≤ 10 9 ) — координаты точек ( x 1 , y 1 ) и ( x 2 , y 2 ) , через которые проходит прямая, разделяющая n точек на белые и чёрные. Точки ( x 1 , y 1 ) и ( x 2 , y 2 ) не должны совпадать.

Примечание

В условии в примере взаимодействия вводимые и выводимые данные расположены для удобства восприятия в хронологическом порядке, при реальном взаимодействии никакие «лишние» переводы строк возникать не должны.

Иллюстрация к первому примеру.

Примеры
Входные данные
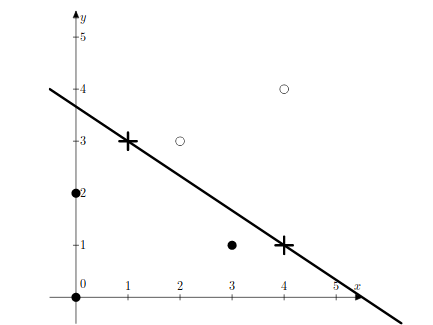
5

black

black

white

white

black
Выходные данные
0 0

3 1

2 3

4 4

0 2

1 3 4 1
#113945
Индра и mex
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
512 megabytes

Индра — большой любитель математики. Читая книгу по теории игр, он наткнулся на интересную функцию \(mex\). Она определяется следующим образом: \(mex(A)\) — это минимальное положительное целое число, которое отсутствует в множестве \(A\). Например, \(mex\) множества \(\{1, 2, 3, 5, 100\}\) равен \(4\), а \(mex\) множества \(\{2, 3, 4, 5\}\) равен \(1\).

Чтобы поупражняться с применением функции \(mex\), Индра взял множество чисел \(A\), состоящее из \(n\) целых положительных чисел, и положительное число \(k\). Затем Индра \(k\) раз произвёл следующую операцию: он добавил в множество \(A\) ещё одно число, равное \(mex(A)\), тем самым, каждый раз увеличивая размер множества \(A\) на один.

По заданному множеству \(A\) и числу \(k\) определите последнее число, которое Индра добавит в множество.

Входные данные

В первой строке заданы два целых числа \(n\) и \(k\) (\(1 \leq n \leq 100\,000\), \(1 \leq k \leq 10^9\)) — количество чисел в множестве и количество операций добавления числа, произведённых Индрой.

Вторая строка содержит \(n\) различных целых чисел \(a_1, a_2, \ldots, a_n\) (\(1 \leq a_i \leq 100\,000\)) — элементы множества \(A\).

Выходные данные

Выведите одно целое число — последнее число, которое Индра добавит в множество.

Примечание

В первом примере \(mex\) множества \(\{1, 2, 4, 5\}\) равен \(3\), после добавления \(mex\) в множество, оно станет равным \(\{1, 2, 3, 4, 5\}\).

Примеры
Входные данные
4 1
4 2 1 5
Выходные данные
3
Входные данные
7 10
1 3 20 2 7 45 5
Выходные данные
15
#114001
Интерактивные смайлики
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
256 megabytes
Это интерактивная задача. Но что самое главное -- это задача про смайлики :) 
 Как известно, смайлики бывают двух типов: веселые и грустные. Каждый день суперкомпьютер Lesli загадывает новый смайлик. Программисты пытаются угадать, какой смайлик загадала Lesli, веселый или грустный. Помогите программистам научиться безошибочно угадывать тип смайлика, который загадала Lesli. Lesli загадывает смайлик на доске размера \(10^9 \times 10^9\). Вся доска заполнена ноликами, кроме тех клеток, в которых расположен загаданный смайлик. Сам смайлик состоит из основы размера \(41 \times 41\), которая приведена ниже. Координаты клеток доски по каждому измерению нумеруются от \(1\) до \(10^9\). Ось \(x\) направлена слева-направо, а ось \(y\) снизу-вверх, как принято в Декартовой системе координат. Так как Lesli не просто компьютер, а суперкомпьютер, она может основу смайлика увеличивать в \(k\) раз, где \(k\) - целое положительное нечетное число. После увеличения в \(k\) раз основа смайлика имеет размер \(41 \cdot k \times 41 \cdot k\). Каждому квадрату \(1 \times 1\) исходной основы соответствует квадрат \(k \times k\) увеличенной основы, если в исходном квадрате стояло число \(0\), то в соответствующем квадрате \(k \times k\) увеличенной основы все числа будут равны \(0\), если в исходном квадрате стояло число \(1\), то в соответствующем квадрате \(k \times k\) увеличенной основы все числа будут равны \(1\). 
После того, как Lesli увеличивает основу смайлика в \(k\) раз, она рисует его в каком то месте доски размера \(10^9 \times 10^9\). Гарантируется, что увеличенный смайлик целиком помещается на доске. Отметим, что у основы смайлика всегда есть центральный квадрат, так как длина стороны основы смайлика всегда нечетна, в том числе после увеличения в нечетное число раз \(k\). 
 После того, как основа смайлика нарисована Lesli рисует ему веселую или грустную улыбку. Форма каждой из улыбок показана под изображением основы смайлика. Слева изображена веселая улыбка, а справа - грустная. В отличие от основы размер исходной улыбки не фиксирован. Улыбку Lesli может увеличить в \(m\) раз, где \(m\) - целое положительное число любой четности. После того, как Lesli увеличивает улыбку смайлика в \(m\) раз, она рисует ее на основе смайлика. Место для улыбки выбирается таким образом, чтобы все квадраты, которые накрыла улыбка, содержали число \(1\). Когда улыбка нарисована, во всех накрытых ею квадратах число \(1\) заменяется на \(0\). Улыбку Lesli рисует таким образом, чтобы все ее квадраты находились ниже, чем центральный квадрат основы смайлика. Кроме того, улыбка рисуется таким образом, чтобы не задеть крайние квадраты основы. Крайние квадраты основы, это такие квадраты, в которых написано число \(1\) и это либо самая нижняя, либо самая верхняя единица в столбце, либо самая правая, либо самая левая единица в строке. Чтобы угадать тип смайлика разрешается сделать не более 500 запросов. Каждый запрос должен задавать некоторый прямоугольник, содержащийся целиком на доске размера \(10^9 \times 10^9\). Ответ на запрос - это количество единичек внутри заданного прямоугольника.

Входные данные
После каждого запроса требуется считать одно число из входных данных (стандартный ввод). Эта число равно количеству единичек в запрашиваемом прямоугольнике.

Выходные данные

Не более 500 раз вы можете сделать запрос - вывести через пробел в одной строке четыре целых числа \(x_1, y_1, x_2, y_2\), \(1 \leq x_1 \leq x_2 \leq 10^9\), \(1 \leq y_1 \leq y_2 \leq 10^9\), -- координаты задающие расположение прямоугольника. После вывода координат необходимо вывести перевод строки и сделать операцию “flush”. После сброса буфера необходимо считать ответ на запрос из входных данных. В любой момент можно перестать делать запросы и вывести число -1, а затем в новой строке вывести “HAPPY” без кавычек, если нарисованный смайлик веселый, или “SAD” без кавычек, если нарисованный смайлик грустный. После этого требуется сделать “flush” и завершить программу. Для сброса буфера вывода (то есть для операции “flush”) сразу после вывода нужно сделать: 
fflush(stdout) в языке C++ 

System.out.flush() в языке Java 

stdout.flush() в языке Python 

flush(output) в языке Pascal
Ваша программа Проверяющая система
1 1 1 1
1 1 1 2
1 2 5 5
-1
HAPPY		 0
0
3


 

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0
0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0
0 0 0 0 0 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 0 0 0 0 0
0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0
0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0
0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0
0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0
0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0
0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0
0 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 0
0 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 0
0 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 0
0 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 0
0 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 0
1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0
0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0
0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0
0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0
0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0
0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0
0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0
0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0
0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0
0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0
0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0
0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0
0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0
0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0                  
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0                         0 0 0 0
  0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0                 0 0 0 0 0 0 0 0 0 0 0 0 0 0
    0 0 0 0 0 0 0 0 0 0 0 0 0 0 	        0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
              0 0 0 0                         0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
                                              0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

Пояснение 
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0
0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0
0 0 0 0 0 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 0 0 0 0 0
0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0
0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0
0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0
0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0
0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0
0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0
0 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 0
0 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 0
0 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 0
0 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 0
0 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 0
1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0
0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0
0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0
0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0
0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0
0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0
0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0
0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0
0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0
0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0
0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0
0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0
0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0
0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0



0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0
0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0
0 0 0 0 0 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 0 0 0 0 0
0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0
0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0
0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0
0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0
0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0
0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0
0 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 0
0 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 0
0 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 0
0 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 0
0 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 0
1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0
0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0
0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0
0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0
0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0
0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0
0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0
0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0
0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0
0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0
0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0
0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0
0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0
0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
Группы тестов

20 баллов. Основа не смещается, улыбка и основа не растягиваются.
10 баллов. Улыбка и основа не растягиваются.
70 баллов. Нет доп. ограничений
#114089
Шарики
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes

Рассмотрим полоску из \(n\) клеточек. На каждой клетке написана какая-то буква латинского языка.

Также каждая клетка изначально содержит \(1\) шарик. Вы последовательно проделываете \(q\) операций следующего вида:

  • "\(c_i\) \(d_i\)" — сдвинуть все шарики, находящиеся в клетке с буквой \(c_i\) в сторону \(d_i\) (\(d_i\) равно или "R" или "L")

Все шарики сдвигаются одновременно. Если какой-то шарик пытается сдвинутся налево из клетки номер \(1\) или направо из клетки \(n\), то он исчезает. Выясните сколько всего останется шариков после выполнения всех операций.

Входные данные

Первая строка содержит целые числа \(n\) и \(q\) (\(1 \le n, q \le 200\,000\)) — длину полоски и количество операций. Следующая строка содержит строку \(s\) длины \(n\), состоящую только из заглавных букв латинского алфавита и задающую буквы в каждой клетке полоски. Оставшиеся \(q\) строк задают операции в виде

  • "\(c_i\) \(d_i\)" — где \(c_i\) является заглавной буквой латинского алфавита, а \(d_i\) или "L", или "R"

Выходные данные

Выведите одно число — количество оставшихся шариков.

Примеры
Входные данные
4 3
BADB
B R
A L
B L
Выходные данные
1
#114114
Вложенные коробки с конфетами
  
ограничение по времени на тест
3.0 second;
ограничение по памяти на тест
512 megabytes

В качестве новогоднего подарка Андрей получил коробку с конфетами. Или не совсем коробку. На самом деле он быстро обнаружил, что внутри коробки находятся ещё несколько одинаковых коробок меньшего размера, внутри которых содержатся ещё меньшие коробки и так далее... Формально, скажем что конфета является коробкой уровня 0 , а коробка уровня i содержит в себе a i коробок уровня i - 1 . Коробка, подаренная Андрею, имеет уровень n .

Сегодня к Андрею в гости придут друзья и он хочет поделиться с ними некоторым количеством конфет, для чего ему придётся открыть некоторое количество коробок. Разумеется, Андрей не может открыть коробку, если она находится внутри ещё не открытой коробки. Ему хотелось бы знать, какое минимальное количество коробок ему потребуется открыть, чтобы достать x конфет. Поскольку Андрей ещё не уверен, сколько друзей к нему сегодня придут, он просит вас решить задачу для нескольких значений x .

Входные данные

В первой строке входных данных записаны числа n и m ( 1 ≤ n , m ≤ 300 000 ) — количество коробок и количество вопросов Андрея соответственно.

Во второй строке записаны n целых чисел a 1 , a 2 , ..., a n ( 1 ≤ a i ≤ 10 9 ).

В третьей строке записаны m чисел x 1 , x 2 ..., x m ( 1 ≤ x i ≤ 10 12 ) — значения количества конфет, для которых Андрей хочет знать ответ. Гарантируется, что каждое значение x i не превосходит общего число конфет в коробке уровня n .

Выходные данные

Выведите m целых чисел, i -е из них должно равняться минимальному количеству коробок, которое потребуется открыть Андрею, чтобы получить хотя бы x i конфет.

Система оценки

Тесты к этой задаче состоят из четырёх групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов некоторых предыдущих групп, указанных в таблице ниже.

Примечание

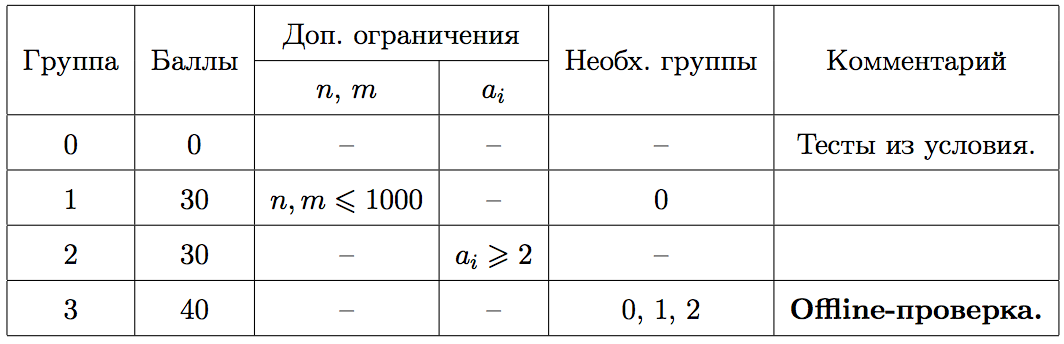
В первом примере единственная конфета спрятана в пяти уровнях коробок.

Во втором примере, чтобы получить 13 конфет, Андрей должен открыть самую большую коробку, затем две коробки уровня 2 , и, наконец, пять из шести имеющихся коробок уровня 1 .

Примеры
Входные данные
5 1
1 1 1 1 1
1
Выходные данные
5
Входные данные
3 3
3 3 3
2 8 13
Выходные данные
3
5
8
Страница: << 25 26 27 28 29 30 31 Отображать по:
Выбрано
:
Отменить
|
Добавить в контест