#111155

Темы: [Линейный поиск] [Алгоритмы сортировки]

Дан список чисел. Определите, есть ли в нем два противоположных(то есть дающих в сумме 0) числа. Если такие числа есть в массиве, выведите их индексы в порядке возрастания. Если таких чисел в массиве нет, ничего не выводите. Гарантируется, что таких пар не больше одной.

Примеры

Входные данные

1 2 3 -2 -4

Выходные данные

1 3

#113096

Призы(2016)

Темы: [Линейный поиск]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Региональный этап, 2016, 1 день, Призы ] [ Личные олимпиады, Всероссийская олимпиада школьников, Региональный этап, 2016, 1 день, Задача A ]

Петя участвует в конкурсе, в котором разыгрывается $n$ призов. Призы пронумерованы от 1 до $n$.

По итогам конкурса участник может набрать от 2 до $n$ баллов. Если участник наберет $k$ баллов, то он получит один из призов с номером от 1 до $k$. Перед тем, как участник выберет свой приз, ведущий конкурса удаляет один из призов из списка. Затем участник может выбрать любой приз из оставшихся $k$ – 1.

Список призов стал известен Пете. Петя определил для каждого приза его ценность, для $i$-го приза она задается целым числом $a_i$ .

Требуется написать программу, которая по заданным ценностям призов определяет для каждого $k$ от 2 до $n$, приз с какой максимальной ценностью гарантированно достанется Пете, если он наберет в конкурсе $k$ баллов.

Входные данные

Первая строка входного файла содержит число $n$ ($2 \le n \le 100 000$). Вторая строка этого файла содержит n целых чисел: $a_1, a_2, …, a_n$ ($1 \le a_i ≤ 10^9$ ).

Выходные данные

Выходной файл должен содержать одну строку, содержащую $n$ – 1 целых чисел: для каждого $k$ от 2 до $n$ должна быть выведена ценность приза, который достанется Пете, если он наберет $k$ баллов.

Описание подзадач и системы оценивания

Баллы за каждую подзадачу начисляются только в случае, если все тесты этой подзадачи успешно пройдены.

Подзадача 1 (24 балла)

$n \le 100$

Подзадача 2 (24 балла)

$n \le 5000$

Подзадача 3 (52 балла)

$n \le 100000$

Примеры

Входные данные

5
1 3 4 2 5

Выходные данные

1 3 3 4

#113887

Чемпионат Юпитера

Темы: [Конструктив] [Линейный поиск]

Как известно, в июне во Флатландии будет проходить чемпионат Юпитера по футболу. В турнире примут участие n команд, а сам турнир будет разыгран в один круг, в ходе которого каждая команда сыграет с каждой другой командой.

На Юпитере выпускают футбольную форму m цветов. Каждая команда привезёт с собой два комплекта формы различных цветов. Разумеется, во время матча все игроки одной команды должны быть одеты в форму одного цвета, отличного от цвета формы другой команды.

Для судейства всех матчей этого чемпионата был приглашён глава Фантастической Инопланетной Футбольной Ассоциации Йозеф. Перед началом матча Йозеф назначает каждой из команд цвет футболок, в которых игроки выйдут на поле. Разумеется, выбирать можно только из тех двух цветов футболок, которые привезла с собой команда. После этого Йозеф выбирает себе футболку какого-то цвета, отличного от обоих цветов, в которых будут играть команды. Таким образом, обе команды и судья будут находиться на поле в футболках разного цвета. Любую футболку и команды, и Йозеф могут использовать в неограниченном количестве игр чемпионата.

Футболки для судейства Йозеф закупает непосредственно перед чемпионатом, опираясь на знание о цветах футболок, привезённых командами на турнир. Поскольку Йозеф экономит деньги своей федерации, он хочет купить себе минимальное количество футболок, такое что их хватит для обслуживания всех матчей. Данная задача слишком сложна для обычного футбольного судьи, поэтому он обратился за помощью к вам.

Входные данные

В первой строке входных данных записаны два числа n и m ( 2 ≤ n ≤ 100 000, 2 ≤ m ≤ 10 ⁹ ) — количество команд, участвующих в чемпионате, и количество возможных цветов футболок.

В i -й из следующих n строк записаны два различных целых числа от 1 до m — цвета футболок, которые привезла с собой команда с номером i .

Выходные данные

В первой строке выведите минимальное количество футболок, которого хватит Йозефу, чтобы обслужить встречи всех пар команд. Если решения не существует, то выведите одну строку содержащую -1 .

В следующей строке выведите цвета этих футболок.

Если оптимальных решений несколько, разрешается вывести любое из них.

Система оценки

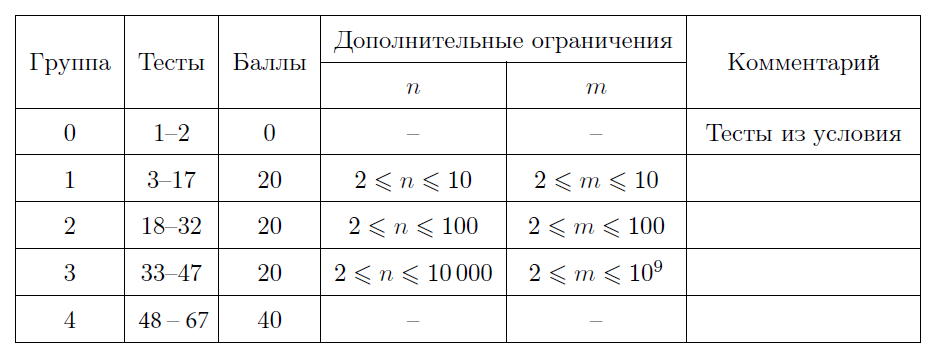
Тесты к этой задаче состоят из пяти групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов предыдущих групп.

$\text{[math]}$

Примеры

Входные данные

Выходные данные

1
1

Входные данные

Выходные данные

2
3 1

#113945

Индра и mex

Темы: [Линейный поиск] [Бинарный поиск по ответу]

Индра — большой любитель математики. Читая книгу по теории игр, он наткнулся на интересную функцию $mex$. Она определяется следующим образом: $mex(A)$ — это минимальное положительное целое число, которое отсутствует в множестве $A$. Например, $mex$ множества $\{1, 2, 3, 5, 100\}$ равен $4$, а $mex$ множества $\{2, 3, 4, 5\}$ равен $1$.

Чтобы поупражняться с применением функции $mex$, Индра взял множество чисел $A$, состоящее из $n$ целых положительных чисел, и положительное число $k$. Затем Индра $k$ раз произвёл следующую операцию: он добавил в множество $A$ ещё одно число, равное $mex(A)$, тем самым, каждый раз увеличивая размер множества $A$ на один.

По заданному множеству $A$ и числу $k$ определите последнее число, которое Индра добавит в множество.

Входные данные

В первой строке заданы два целых числа $n$ и $k$ ($1 \leq n \leq 100\,000$, $1 \leq k \leq 10^9$) — количество чисел в множестве и количество операций добавления числа, произведённых Индрой.

Вторая строка содержит $n$ различных целых чисел $a_1, a_2, \ldots, a_n$ ($1 \leq a_i \leq 100\,000$) — элементы множества $A$.

Выходные данные

Выведите одно целое число — последнее число, которое Индра добавит в множество.

Примечание

В первом примере $mex$ множества $\{1, 2, 4, 5\}$ равен $3$, после добавления $mex$ в множество, оно станет равным $\{1, 2, 3, 4, 5\}$.

Примеры

Входные данные

4 1
4 2 1 5

Выходные данные

Входные данные

7 10
1 3 20 2 7 45 5

Выходные данные