Бинарный поиск по ответу(56 задач)
Бинарный поиск значения функции(5 задач)
С утра шел дождь, и ничего не предвещало беды. Но к обеду выглянуло солнце, и в лагерь заглянула СЭС. Пройдя по всем домикам и корпусам, СЭС вынесла следующий вердикт: бельевые веревки в жилых домиках не удовлетворяют нормам СЭС. Как выяснилось, в каждом домике должно быть ровно по одной бельевой веревке, и все веревки должны иметь одинаковую длину. В лагере имеется \(N\) бельевых веревок и \(K\) домиков. Чтобы лагерь не закрыли, требуется так нарезать данные веревки, чтобы среди получившихся веревочек было \(K\) одинаковой длины. Размер штрафа обратно пропорционален длине бельевых веревок, которые будут развешены в домиках. Поэтому начальство лагеря стремиться максимизировать длину этих веревочек.
В первой строке заданы два числа — \(N\) (\(1 \le N \le 10001\)) и \(K\) (\(1 \le K \le 10001\)). Далее в каждой из последующих \(N\) строк записано по одному числу — длине очередной бельевой веревки. Длина веревки задана в сантиметрах. Все длины лежат в интервале от \(1\) сантиметра до \(100\) километров включительно.
В выходной файл следует вывести одно целое число — максимальную длину веревочек, удовлетворяющую условию, в сантиметрах. В случае, если лагерь закроют, выведите \(0\).
4 11 802 743 457 539
200
Найдите такое число \(x\), что \(x^2 + \sqrt{x} = C\), с точностью не менее \(6\) знаков после точки.
В единственной строке содержится вещественное число \(1.0 \le C \le 10^{10}\).
Выведите одно число — искомый \(x\).
2.0000000000
1.000000000
18.0000000000
4.000000000
Уже долгое время в Институте Искусств, Мутантов и Информационных Технологий разводят милых разноцветных зверюшек. Для удобства каждый цвет обозначен своим номером, всего цветов не более \(10^9\). В один из прекрасных дней в питомнике случилось чудо: все зверюшки выстроились в ряд в порядке возрастания цветов. Пользуясь случаем, лаборанты решили посчитать, сколько зверюшек каждого из запрошенных цветов живет в питомнике, и, по закону жанра, попросили вас написать программу, которая поможет им в решении этой нелегкой задачи.
В первой строке входного файла содержится единственное число \(N\) (\(0 \le N \le 10^5\)) — количество зверюшек в Институте. В следующей строке находятся \(N\) упорядоченных по неубыванию неотрицательных целых чисел, не превосходящих \(10^9\) и разделенных пробелами — их цвета. В третьей строке файла записано число \(M\) (\(1 \le M \le 100\,000\)) — количество запросов вашей программе, в следующей строке через пробел записаны \(M\) целых неотрицательных чисел (не превышающих \(10^9+1\)).
Выходной файл должен содержать \(M\) строчек. Для каждого запроса выведите число зверюшек заданного цвета в питомнике.
10 1 1 3 3 5 7 9 18 18 57 5 57 3 9 1 179
1 2 1 2 0
На краю деревни растет старая березовая аллея. Аллея имеет форму прямой полосы шириной \(W\) метров. Вдоль левой стороны аллеи растет \(N\) берез, а вдоль правой — \(M\) берез, при этом \(i\)-я береза с левой стороны аллеи находится на расстоянии \(a_i\) метров от начала аллеи, а \(j\)-я береза с правой стороны — на расстоянии \(b_j\) метров от начала аллеи.
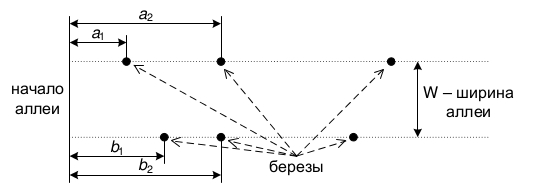
Отдыхая в деревне прошедшим летом, один юный информатик обнаружил, что кору берез стали грызть зайцы. Чтобы защитить деревья от зайцев, мальчик решил окружить березы красной лентой (зайцы не любят красный цвет и не станут заходить на огражденную лентой территорию. К сожалению, в его распоряжении оказалась только лента длиной \(L\) метров, которую, к тому же, нельзя было разрезать. Единственное, что можно было делать в этом случае — окружить этой лентой как можно больше берез. При этом, чтобы сохранить аллею, необходимо окружить на каждой стороне аллеи хотя бы одну березу.
Требуется написать программу, которая по заданной длине ленты, ширине аллеи и положению берез на ней определяет максимальное число берез, которое можно окружить этой лентой. Считается, что березы представляются точками, толщиной берез и шириной ленты следует пренебречь.
Первая строка входного файла содержит два разделенных пробелом целых числа: длину ленты \(L\) и ширину аллеи \(W\) (\(1 \leq L \leq 2 \times 10^5\), \(1 \leq W \leq 10^4\)).
Вторая и третья строки описывают березы вдоль левой стороны аллеи. Вторая строка содержит число \(N\) — количество берез (\(1 \leq N \leq 2000\)), а третья строка содержит \(N\) различных целых чисел \(a_1\), \(a_2\), …, \(a_N\) (\(0 \leq a_i \leq 10^5\)), заданных по возрастанию.
Четвертая и пятая строки описывают березы вдоль правой стороны аллеи. Четвертая строка содержит число \(M\) — количество берез (\(1 \leq M \leq 2000\)), а пятая строка содержит \(M\) различных целых чисел \(b_1\), \(b_2\), …, \(b_M\) (\(0 \leq b_i ≤ 10^5\)), заданных по возрастанию.
Выходной файл должен содержать одно целое число: максимальное количество берез, которое можно оградить заданной лентой.
Гарантируется, что если максимальное число берез, которое можно оградить лентой длины L, равно X, то нет способа оградить (X + 1) березу лентой длины (L + \(10^{-5}\)).
Правильные решения для тестов, в которых 1 ≤ N + M ≤ 50, будут оцениваться из 30 баллов.
Правильные решения для тестов, в которых 1 ≤ N + M ≤ 500, будут оцениваться из 60 баллов.
18 4 3 0 3 6 4 0 3 6 10
5
5 3 1 0 1 0
0
| Ограничение по времени, сек | 0.75 |
| Ограничение по памяти, мегабайт | 256 |
Министерство обороны Флатландии планирует построить новый военный полигон. Полигон должен иметь форму круга.
Поскольку генералы в министерстве волнуются о секретности проводимых на полигоне испытаний, он должен быть надежно защищен. Флатландия защищена сверху несколькими специальными силовыми щитами, каждый из них имеет форму прямоугольника со сторонами, параллельными осям координат. Генералы хотят выбрать такое место для полигона, где он был бы полностью защищен хотя бы двумя конкретными силовыми щитами (недостаточно, чтобы каждая точка просто была защищена хотя бы двумя щитами, должно быть два щита, каждый из которых защищает полигон полностью).
Конечно, генералы хотят построить полигон максимального возможного размера. Помогите им выбрать такое место для полигона, чтобы он имел максимальный возможный радиус.
Первая строка входного файла содержит число \(N\) — количество силовых щитов. Каждая из следующих N строк описывает силовой щит (\(1 \leq N \leq 200000\)). Описание представляет собой четверку координат: \(x_{min}\), \(y_{min}\), \(x_{max}\), \(y_{max}\). Все координаты целые и не превышают 100000 по абсолютной величине.
Выведите три вещественных числа — координаты центра полигона и его радиус. Все числа следует выводить ровно с одним знаком после десятичной точки.
Если построить полигон невозможно, выведите “Impossible” на первой строке выходного файла.
4 0 0 2 3 1 -1 4 1 1 1 4 4 2 0 5 5
3.0 2.0 1.0
1 0 0 1 1
Impossible
2 0 0 3 3 0 0 3 3
1.5 1.5 1.5