Алгоритм Флойда(20 задач)
Обход в ширину(62 задач)
Алгоритм Форда-Беллмана(6 задач)
В подземелье есть N залов, соединенных туннелями. В некоторых залах находятся роботы, которые одновременно получили команду собраться в одном месте.
Роботы устроены так, что, получив команду, они все начали двигаться с такой скоростью, что туннель между двумя любыми залами преодолевают за 1 минуту. Роботы не могут останавливаться (в том числе и в залах), а также менять направление движения, находясь в туннелях (однако попав в зал, робот может из него пойти по тому же туннелю, по которому он пришел в этот зал).
Напишите программу, вычисляющую, через какое минимальное время все роботы смогут собраться вместе (в зале или в туннеле).
Сначала на вход программы поступают числа N — количество залов (1≤N≤400) и K — количество туннелей (1≤K≤20000). Далее вводится K пар чисел, каждая пара описывает номера залов, соединяемых туннелем (по туннелю можно перемещаться в обе стороны). Между двумя залами может быть несколько туннелей. Туннель может соединять зал с самим собой. Далее следует число M (1≤M≤400) — количество роботов. Затем вводятся M чисел, задающих номера залов, где вначале расположены роботы. В одном зале может быть несколько роботов.
Выведите минимальное время в минутах, через которое роботы могут собраться вместе. Если роботы никогда не смогут собраться вместе, выведите одно число –1 (минус один).
Оценка задачи
1 балл получат программы, правильно решающие задачу в случае, когда встреча роботов произойдет в зале, при ограничениях N≤100, K≤2000, M≤100.
4 5 1 2 2 3 3 4 1 4 1 3 3 1 2 4
1
3 2 1 2 2 3 2 1 3
1
На плоскости нарисовали прямоугольник, после чего его разрезали прямыми. Напишите программу, которая вычислит, сколько из полученных кусков исходного прямоугольника имеют треугольную форму.
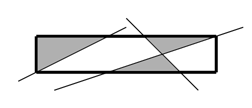
Рисунок, соответствующий 1-му примеру входных и выходных данных
Сначала на вход программы поступают два положительных числа X и Y, задающих координаты правого верхнего угла прямоугольника. Прямоугольник расположен в системе координат так, что левый нижний его угол имеет координаты 0,0 и стороны параллельны осям координат.
Далее вводится целое число N — количество разрезов (1≤N≤200). Затем описываются сами разрезы. Каждый разрез делался вдоль некоторой прямой. Каждая прямая, соответствующая разрезу, задается тремя числами A, B, C такими, что все точки (x,y) этой прямой (и только они) удовлетворяют уравнению Ax+By+C=0 (при этом всегда A2+B2>0).
Все входные данные (кроме N) – вещественные числа, заданы с двумя знаками после десятичной точки и не превышают 104. Никакие две прямые не совпадают между собой и не содержат сторон прямоугольника. Каждый разрез проходит через точки внутри исходного прямоугольника.
Выведите одно целое число — количество частей исходного прямоугольника, имеющих треугольную форму.
Система оценки
1 балл получат программы, правильно решающие задачу при ограничении 1≤N≤50.
5.00 1.00 3 1.00 -2.00 0.00 1.00 -3.00 -2.00 1.00 1.00 -4.00
3
4.00 2.00 2 1.00 -2.00 0.00 1.00 2.00 -4.00
4
Дан ориентированный граф, рёбрам которого приписаны некоторые неотрицательные веса (длины). Найти длину кратчайшего пути из вершины s в вершину t.
В первой строке заданы три числа: число вершин в графе N ≤50, номера вершин s и t. Далее идёт матрица смежности графа, то есть N строк, в каждой из которых записано N чисел. j-ое число в i-ой строке матрицы смежности задает длину ребра, ведущего из i-й вершину в j-ую. Длины могут принимать любые значения от 0 до 1000000, число -1 означает отсутствие соответствующего ребра. Гарантируется, что на главной диагонали матрицы стоят нули.
Выведите одно число – минимальную длину пути. Если пути не существует, выведите -1.
3 1 2 0 -1 3 7 0 1 2 -1 0
-1
Дан ориентированный граф, рёбрам которого приписаны некоторые неотрицательные веса (длины). Надо найти две вершины, кратчайший путь между которыми имеет наибольшую длину.
В первой строке задано число вершин N ≤50. Далее идёт матрица смежности графа, то есть N строк, в каждой из которых записано N чисел. j-ое число в i-ой строке матрицы смежности задает длину ребра, ведущего из i-й вершину в j-ую. Длины могут принимать любые значения от от 0 до 1000000. Гарантируется, что на главной диагонали матрицы стоят нули.
Выведите одно число – длину искомого пути.
3 0 7 3 7 0 10 2 215 0
10
Дан ориентированный полный граф, рёбрам которого приписаны некоторые веса (длины). Веса могут быть и положительные, и отрицательные, и нулевые. Нас интересует минимум длин всех возможных путей между всеми парами различных вершин этого графа. Нужно будет выяснить, существует ли этот минимум, и, если существует, вычислить его. (Минимума не существует в том случае, если в графе можно найти путь отрицательной длины, сколь угодно большой по модулю).
В первой строке задано число вершин N≤50. Далее идёт матрица смежности графа, то есть N строк, в каждой из которых записано N чисел. j-ое число в i-ой строке матрицы смежности задает длину ребра, ведущего из i-й вершину в j-ую. Длины могут принимать любые значения от -1000000 до 1000000. Гарантируется, что на главной диагонали матрицы стоят нули.
Выведите одно число – искомый минимум. Если его не существует, выведите -1.
3 0 42 18468 6335 0 26501 19170 15725 0
42
3 0 -7 3 -2 0 10 2 215 0
-1