Массивы(232 задач)
Типы данных(356 задач)
Циклы(177 задач)
Условный оператор (if)(164 задач)
Python(260 задач)
Standard Template Library(2 задач)
Компания RectanGas занимается добычей нефти уже с незапяматных времен и является бесспорным лидером в своей области. Маркетологи считают, что она стала такой успешной благодаря бессменному исполнительному директору. На нем стоит остановиться поподробнее.
Дело в том, что исполнительный директор совсем не изучал геометрию в школе и до сих пор считает, что кроме прямоугольников других геометрических фигур не существует. Более того, он никак не может поверить, что стороны прямоугольников могут быть не параллельными осям координат. Поэтому все нефтяные вышки строятся следующим образом: директор на карте отмечает четыре точки так, чтобы они образовывали прямоугольник со сторонами, параллельными осям координат карты, и приказывает строить нефтяные вышки на участках, соответствующим отмеченным точкам на карте. Эти нефтяные вышки за короткий промежуток времени добывают всю нефть, расположенную на соответствующем участке.
Компания RectanGas почти выполнила свой план по добыче нефти на май 2010 года. Для этого ей осталось добыть ровно S баррелей нефти. Заметим, что больше добывать нельзя, иначе компанию обвинят в монополии. Меньше добывать тоже нельзя, потому что исполнительный директор, будучи человеком пунктуальным, очень огорчится, что повлечет за собой увольнение сотрудников и всеобщую безработицу. Геологи, подробно изучив карту местности, определили количество залежей нефти на каждом участке и попросили Вас написать программу, определяющую координаты будущих нефтяных вышек с учетом всех требований.
Первая строка содержит три числа: размеры карты местности n и m и план по добыче нефти S ( 2 ≤ n , m ≤ 300 ; 0 ≤ S ≤ 10 7 ). Далее следуют n строк по m чисел a ij — количество залежей нефти на соответсвующем участке ( 0 ≤ a ij ≤ 10 6 )
В случае, если увольнения не миновать, выведите « - 1 » (без кавычек). В противном случае выведите четыре числа — координаты левой верхней и правой нижней вышек соответственно. Если вариантов ответа несколько, то выведите любой из них.
Обратите внимание, в этой задаче TL равен 500 мс.
Иллюстрация к первому примеру:
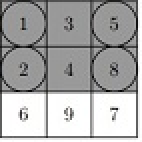
Сумма значений в угловых вышках равна 1 + 5 + 2 + 8 = 16
3 3 16 1 3 5 2 4 8 6 9 7
1 1 2 3
2 3 4 12 6 7 4 9 5
-1
В стране Байтландии есть n городов, соединенных дорогами. Каждая дорога двухсторонняя и имеет некоторую длину. Также, в стране есть две партии — одна выступает за то, что вилку необходимо держать во время еды в левой руке, другая — за то, что вилку необходимо держать в правой руке. В каждый момент времени каждый из городов поддерживает только одну партию. Вот только время от времени в городах происходят перевороты и в одном из городов поддерживаемая партия меняется на противоположную.
Правительство Байтландии поручило Вам написать программу, которая бы в каждый момент времени оценивала стабильность политической ситуации в стране. Согласно математической модели, разработанной ведущими учеными Байтландии, стабильность зависит от того, насколько близко находятся города, поддерживающие одну и ту же партию, поскольку чем ближе они, чем больше вероятность того, что они могут объединиться в коалицию.
Поэтому программа, написанная Вами, должна по информации о всех городах, дорогах и происходящих переворотах находить, после каждого переворота, два города, поддерживающих одну партию, и находящихся на наименьшем расстоянии друг от друга.
Первая строка входного файла содержит три целых числа n, m и k (1 ≤ n, m, k ≤ 100000) — количество городов, дорог и переворотов соответственно.
Вторая строка содержит строку s длиной n, описывающую политическую ситуацию в стране на момент начала наблюдения. Символ L на i-ой позиции означает, что город номер i поддерживает партию, выступающую за то, что вилку необходимо держать в левой руке, символ R — в правой.
Следующие m строк содержат по три целых числа ai, bi и li (1 ≤ ai, bi ≤ n, ai ≠ bi, 1 ≤ li ≤ 109) — номера городов, которые соединены i-ой дорогой и ее длина. Каждая пара городов соединена не более, чем одной дорогой.
В последней строке содержится k чисел --- номера городов cj (1 ≤ cj ≤ n), в которых происходили перевороты в порядке их происшествия. Поскольку все города достаточно консервативны, то в каждом городе произошло не более одного переворота, то есть все cj различны.
В выходной файл выведите k + 1 отчет о ближайших городах, которые могут объединиться в коалицию. Первое описание должно соответствовать началу наблюдения, каждое следующее — после очередного переворота в одном из городов.
Каждое описание должно быть выведено на отдельной строке и содержать три целых числа di, xi и yi — минимальное расстояния между городами, поддерживающими одну партию и номера этих городов, соответственно. Если таких пар несколько, выведите любую. Гарантируется, что хотя бы одна такая пара всегда существует.
n ≤ 100. Решение оценивается в 30 баллов.
Дополнительные ограничения отсутствуют. Решение оценивается в 40 баллов.
5 6 4 LRLRL 1 4 1 2 3 2 3 4 3 4 5 4 2 5 5 2 4 6 1 4 3 5
4 1 3 1 1 4 3 3 4 2 2 3 2 2 3
Петя и Вася — одноклассники и лучшие друзья, поэтому они во всём помогают друг другу. Завтра у них контрольная по математике, и учитель подготовил целых K вариантов заданий.
В классе стоит один ряд парт, за каждой из них (кроме, возможно, последней) на контрольной будут сидеть ровно два ученика. Ученики знают, что варианты будут раздаваться строго по порядку: правый относительно учителя ученик первой парты получит вариант 1, левый — вариант 2, правый ученик второй парты получит вариант 3 (если число вариантов больше двух) и т.д. Так как K может быть меньше чем число учеников N, то после варианта K снова выдаётся вариант 1. На последней парте в случае нечётного числа учеников используется только место 1.
Петя самым первым вошёл в класс и сел на своё любимое место. Вася вошёл следом и хочет получить такой же вариант, что и Петя, при этом сидя к нему как можно ближе. То есть между ними должно оказаться как можно меньше парт, а при наличии двух таких мест с равным расстоянием от Пети Вася сядет позади Пети, а не перед ним. Напишите программу, которая подскажет Васе, какой ряд и какое место (справа или слева от учителя) ему следует выбрать. Если же один и тот же вариант Вася с Петей писать не смогут, то выдайте одно число - 1.
В первой строке входных данных находится количество учеников в классе 2 ≤ N ≤ 109. Во второй строке — количество подготовленных для контрольной вариантов заданий 2 ≤ K ≤ N. В третьей строке — номер ряда, на который уже сел Петя, в четвёртой — цифра 1, если он сел на правое место, и 2, если на левое.
Если Вася никак не сможет писать тот же вариант, что и Петя, то выведите - 1. Если решение существует, то выведите два числа — номер ряда, на который следует сесть Васе, и 1, если ему надо сесть на правое место, или 2, если на левое. Разрешается использовать только первые N мест в порядке раздачи вариантов.
25
2
1
2
2 2
25
13
7
1
-1
В первом примере вариантов 2, поэтому наилучшее место для Васи находится сразу за Петей. Во втором примере Петя будет единственным, кто получит вариант 13.
Каждый тест в задаче оценивается отдельно. Программа, выдающая правильный ответ только на тесты из условия и тесты с ответом - 1, не оценивается. Решение тестируется на основном наборе тестов только при прохождении всех тестов из условия. При этом тесты из условия не оцениваются.
Подзадача 1. N ≤ 100. Оценивается из 52 баллов.
Подзадача 2. N ≤ 109. Оценивается из 48 баллов.
На день рождения маленький Ипполит получил долгожданный подарок — набор дощечек с написанными на них буквами латинского алфавита. Теперь-то ему будет чем заняться долгими вечерами, тем более что мама обещала подарить ему в следующем году последовательность целых неотрицательных чисел, если он хорошо освоит этот набор. Ради такого богатства Ипполит готов на многое.
Прямо сейчас юный исследователь полностью поглощён изучением хорошести строк. Хорошестью строки называется количество позиций от 1 до L - 1 (где L — длина строки), таких, что следующая буква в строке является следующей по алфавиту. Например, хорошесть строки "abcdefghijklmnopqrstuvwxyz" равна 25, а строки "abdc" — только 1.
Ипполит размышляет над решением закономерно возникающей задачи: чему равна максимально возможная хорошесть строки, которую можно собрать, используя дощечки из данного набора? Вы-то и поможете ему с ней справиться.
Первая строка ввода содержит единственное целое число N — количество различных букв в наборе (1 ≤ N ≤ 26). Обратите внимание: в наборе всегда используются N первых букв латинского алфавита.
Следующие N строк содержат целые положительные числа ci — количество букв соответствующего типа (1 ≤ ci ≤ 109). Таким образом, первое число означает количество букв "a", второе число задаёт количество букв "b" и так далее.
Выведите единственное целое число — максимально возможную хорошесть строки, которую можно собрать из имеющихся дощечек.
3
1
1
1
2
2
3
4
3
В первом тесте имеется по одной дощечке с каждой из 3 различных букв. Ответ 2 достигается на строке "abc"
Каждый тест в данной задаче оценивается отдельно. Решение тестируется на основном наборе тестов только при прохождении всех тестов из условия. При этом тесты из условия не оцениваются.
Подзадача 1. Во всех тестах данной группы ci ≤ 100. Данная подзадача оценивается из 40 баллов.
Подзадача 2. Во всех тестах данной группы ci ≤ 1 000 000. Данная подзадача оценивается из 30 баллов.
Подзадача 3. Во всех тестах данной группы ci ≤ 109. Данная подзадача оценивается из 30 баллов.
Летом Максим съездил в Летнюю Какую-то Школу, где, помимо учёбы, ему очень запомнилась игра «Шляпа», в которую он вместе с друзьями играл всю смену. Опишем правила игры, которых они придерживались. Обратите внимание: эти правила немного отличаются от общепринятых.
Изначально в шляпу помещают некоторое количество бумажек с написанными на них словами. После этого команды из двух человек по очереди и в случайном порядке начинают отгадывать слова - один член команды объясняет другому написанное на бумажке слово, не используя однокоренные. Если партнёр отгадывает его, то команде засчитывается одно очко, слово выкидывается, а команда достаёт из шляпы новое, если у неё ещё осталось время в этом раунде. Если команда не успевает отгадать очередное слово, то бумажка на которой оно написано, возвращается в шляпу, и ход передаётся какой-то случайной команде, возможно, той же самой. Игра продолжается, пока все слова из шляпы не будут отгаданы.
Теперь Максим провёл турнир для N команд из своей школы и должен определить победителя. Он неаккуратно вёл записи игры и не отмечал, сколько слов отгадала каждая из команд, зато он записывал в хронологическом порядке каждый раз, когда какая-либо команда доставала какую-либо бумажку из шляпы. Всего таких записей M, и они следуют в хронологическом порядке. Помогите Максиму восстановить по сделанным записям, сколько слов отгадала каждая из команд.
В первой строке дано количество команд N и количество попыток отгадать слова M (1 ≤ N ≤ 100 000, 1 ≤ M ≤ 100 000). В следующих M строках сначала указывается номер ni команды, пытавшейся отгадать слово, а через пробел дано слово wi, написанное на бумажке. Номера команд лежат в диапазоне от 1 до N. Все слова wi состоят из строчных латинских букв и имеют ненулевую длину, не превосходящую 10 букв.
Выведите в одну строку N чисел, i-ое число должно равняться количеству слов, отгаданному i-ой командой.
2 3
1 hat
1 shirt
2 hat
1 1
3 2
1 mom
3 dad
1 0 1
В первом примере первая команда отгадала слово shirt, а вторая слово hat.
Каждый тест в данной задаче оценивается отдельно. Решение тестируется на основном наборе тестов только при прохождении всех тестов из условия. При этом тесты из условия не оцениваются.
Подзадача 1. 1 ≤ N ≤ 2000, 1 ≤ M ≤ 2000. Каждое слово встречается только один раз. Оценивается из 20 баллов.
Подзадача 2. 1 ≤ N ≤ 2000, 1 ≤ M ≤ 2000. Оценивается из 30 баллов.
Подзадача 3. 1 ≤ N ≤ 100 000, 1 ≤ M ≤ 100 000. Оценивается из 50 баллов.