>Во время исследований, посвященных появлению жизни на планете Олимпия, учеными было сделано несколько сенсационных открытий:
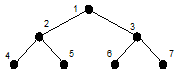
Чтобы не придумывать названия во время исследований, ученые пронумеровали все виды организмов, которые когда-либо существовали на планете. Для этого они нарисовали дерево эволюции с корнем Bitozoria Programulis, которая получила номер 1. Далее нумеровали виды каждого шага эволюции слева направо. Таким образом непосредственные подвиды Bitozoria Programulis получили номера 2 и 3. Следующими были занумерованы виды третьего шага эволюции – подвиды вида 2 получили номера 4 и 5, а вида 3 – номера 6 и 7, и т.д.
Напишите программу, которая по номерам двух видов вычислит номер вида их ближайшего общего предка в дереве эволюции.
Первая строка входного файла содержит целое число N (1≤N≤100) – количество этапов эволюции, которые произошли на планете Олимпия до текущего времени. Вторая и третья строки файла содержат по одному натуральному числу, которые представляют номера видов, для которых требуется найти номер их ближайшего общего предка.
Единственная строка выходного файла должна содержать натуральное число – номер ближайшего предка для двух видов.
4 15 12
3
18 233016 233008
14563
Васин жесткий диск состоит из \(M\) секторов. Вася последовательно устанавливал на него различные операционные системы следующим методом: он создавал новый раздел диска из последовательных секторов, начиная с сектора номер \(a_i\) и до сектора \(b_i\) включительно, и устанавливал на него очередную систему. При этом если очередной раздел хотя бы по одному сектору пересекается с каким-то ранее созданным разделом, то ранее созданный раздел «затирается», и операционная система, которая на него была установлена, больше не может быть загружена.
Напишите программу, которая по информации о том, какие разделы на диске создавал Вася, определит, сколько в итоге работающих операционных систем установлено и в настоящий момент работает на Васином компьютере.
Сначала вводятся натуральное число \(M\) — количество секторов на жестком диске (1 ≤ \(M\) ≤ \(10^9\)) и целое число \(N\) — количество разделов, которое последовательно создавал Вася (0 ≤ \(N\) ≤ 100 000).
Далее идут \(N\) пар чисел \(a_i\) и \(b_i\), задающих номера начального и конечного секторов раздела (1 ≤ \(a_i\) ≤ \(b_i\) ≤ \(M\)).
Выведите одно число — количество работающих операционных систем на Васином компьютере.
10 3 1 3 4 7 3 4
1
Ограничение по времени: 0.2 секунды
На планете Олимпия рабочие строят новую дамбу. Часть плоскости, на которой проводятся строительные работы, имеет вид прямоугольника размером 1 x \(L\) метров, на котором введены координаты, как показано на рисунке.
Для поднятия ландшафта используют специально разработанные магические импульсаторы. Если магический импульсатор силой \(H\) поставить в точку с \(X\)-координатой \(p\), то в каждой точке \(q\) отрезка [\(p\)–\(H\);\(p\)] на оси \(X\) рельеф поднимается на \(q\)–\(p\)+\(H\) метров по всей его ширине (то есть для произвольного \(Z\) от 0 до 1), а в каждой точке \(q\) отрезка [\(p\);\(p\)+\(H\)] рельеф поднимается на \(H\)+\(p\)–\(q\) метров по всей его ширине, в остальных точках ландшафт остается неизменным (см. рисунок).
Во время строительства рабочие время от времени интересуются объёмом части дамбы, находящейся над некоторым прямоугольником.
Напишите программу, которая поможет рабочим в их расчётах.
В первой строке входного файла содержатся два целых числа: N – количество операций, которые будут выполнять рабочие (1≤\(N\)≤100000), и \(L\) – длина прямоугольника (1≤\(L\)≤100000).
В следующих \(N\) строках содержатся описания операций: первое число строки – номер операции, где „1” означает, что рабочие собираются поставить магический импульсатор, „2” – рабочие хотят узнать некоторый объём. Если операция имеет код „1”, то далее идут два целых числа \(p\) и \(H\) (0≤\(p\)≤\(L\); 1≤\(H\)≤\(L\)), то есть импульсатор силой \(H\) ставят в позицию p (на оси \(X\)). Если операция имеет код „2”, то далее идут два целых числа \(A\) и \(B\) (0≤\(A\)<\(B\)≤\(L\)); это означает, что рабочие хотят узнать объём части дамбы, которая находится над прямоугольником от \(A\) до \(B\) по оси \(X\), и от 0 до 1 по оси \(Z\).
Создайте выходной файл, в котором для каждой операции, указанной во входном файле, выведите строку со следующей информацией.
Если операция есть „1”, то выведите число „-1” без кавычек. Если операция есть „2”, то выведите число округленное вниз до ближайшего целого, равное объёму части дамбы, которая находится над прямоугольником от \(A\) до \(B\) по оси \(X\), и от 0 до 1 по оси \(Z\), как показано на рисунке.
2 13 1 7 5 2 5 9
-1 16
Маленький мальчик делает бусы. У него есть много пронумерованных бусинок. Каждая бусинка имеет уникальный номер – целое число в диапазоне от 1 до N. Он выкладывает все бусинки на полу и соединяет бусинки между собой произвольным образом так, что замкнутых фигур не образуется. Каждая из бусинок при этом оказывается соединенной с какой-либо другой бусинкой.
Требуется определить, какое максимальное количество последовательно соединенных бусинок присутствует в полученной фигуре (на рисунке эти бусинки выделены темным цветом).
Формат входных данных
В первой строке – количество бусинок 1≤N≤2500. В последующих N-1 строках по два целых числа – номера, соединенных бусинок.
Формат выходных данных
Вывести одно число – искомое количество бусинок.
Пример
| Входные данные | Выходные данные |
| 7 4 5 6 7 7 4 7 2 1 3 4 1 | 5 |
Дана последовательность N прямоугольников различной ширины и высоты (wi,hi). Прямоугольники расположены, начиная с точки (0, 0), на оси ОХ вплотную друг за другом (вправо). Требуется найти M - площадь максимального прямоугольника (параллельного осям координат), который можно вырезать из этой фигуры.
Формат входных данных
В первой строке задано число N (1 ≤ N ≤ 8000). Далее идет N строк. В каждой строке содержится два числа: ширина и высота i-го прямоугольника. Значение 
, 0 < hi ≤ 3*104.
Формат выходных данных
Вывести одно число М. Значение M не превосходит 2*109.
3 4 3 2 1 2 5
12
3 4 3 2 1 3 5
15