Двоичное дерево поиска(24 задач)
Дерево отрезков, RSQ, RMQ(90 задач)
Бор(14 задач)
Дерево Фенвика(6 задач)
Декартово дерево(10 задач)
Строка s называется супрефиксом для строки t, если t начинается с s и заканчивается на s. Например, «abra» является супрефиксом для строки «abracadabra». В частности, сама строка t является своим супрефиксом. Супрефиксы играют важную роль в различных алгоритмах на строках.
В этой задаче требуется решить обратную задачу о поиске супрефикса, которая заключается в следующем. Задан словарь, содержащий n слов t1, t2, …, tn и набор из m строк-образцов s1, s2, …, sm. Необходимо для каждой строки-образца из заданного набора найти количество слов в словаре, для которых эта строка-образец является супрефиксом.
Требуется написать программу, которая по заданному числу n, n словам словаря t1, t2, …, tn, заданному числу m и m строкам-образцам s1, s2, …, sm вычислит для каждой строки-образца количество слов из словаря, для которых эта строка-образец является супрефиксом.
Первая строка входного файла содержит целое число n (1 ≤ n ≤ 200 000).
Последующие n строк содержат слова t1, t2, …, tn, по одному слову в каждой строке. Каждое слово состоит из строчных букв латинского алфавита. Длина каждого слова не превышает 50. Суммарная длина всех слов не превышает 106. Словарь не содержит пустых слов.
Затем следует строка, содержащая целое число m (1 ≤ m ≤ 200 000).
Последующие m строк содержат строки-образцы s1, s2, …, sm, по одной на каждой строке. Каждая строка-образец состоит из строчных букв латинского алфавита: Длина каждой строки-образца не превышает 50. Суммарная длина всех строк-образцов не превышает 106. Никакая строка-образец не является пустой строкой.
Выходной файл должен содержать m чисел, по одному на строке.
Для каждой строки-образца в порядке, в котором они заданы во входном файле, следует вывести количество слов словаря, для которых она является супрефиксом.
Решения, работающие при \(n\), \(m\) не превосходящими 100 оцениваются из 30 баллов.
4 abacaba abracadabra aa abra 3 a abra abac
4 2 0
Город Прямой Рог, который пока что не находится на территории Российской Федерации, представляет собой одну прямую улицу. В городе работает компания, которая занимается доставкой товаров. Для удобства, адреса доставки представлены в виде чисел, которые задают расстояние от офиса компании. Положительные числа в одну сторону, а отрицательные – в другую. Заказы на доставку выполняются компанией последовательно, в том порядке, в котором они были заданы. В компании работает два курьера. В начале рабочего дня заказы распределяются между ними, и каждый отправляется по своему маршруту. Компании необходимо так спланировать распределение заказов, чтобы суммарное расстояние, которое будет пройдено курьерами на момент выполнения последнего заказа, была минимальным. Напишите программу, которая по расстояниям адресатов от офиса компании находит наименьшее суммарное расстояние, которое пройдут ее работники.
Первая строка входных данных содержит целое число N (1 ≤ N ≤ 100 000) — количество заказов. Далее следует N строк, каждая из которых содержит одно целое число — расстояние от офиса до адресата. Если расстояние положительное — то адресат находится в одной части города относительно офиса компании, а если отрицательное, то в другой. Расстояния по модулю не превышают 108.
Единственная строка должна содержать одно целое число — минимально возможное суммарное расстояние, которое пройдут оба работника компании.
5
1
-1
2
-2
3
5
Все элементы магнитной мозаики фирмы «ABBYY» имеют прямоугольную форму. Два элемента можно соединить только в том случае, если у них совпадает хотя бы один из размеров: длина, ширина, или и то, и другое. Магнитные элементы поворачивать и переворачивать нельзя. Пару элементов мозаики, которые нельзя соединить, назовем негармоничной. Например, пара 1 × 2 и 2 × 3 является негармоничной, а пары 2 × 3 и 1 × 3 или 2 × 3 и 2 × 3 являются гармоничными. Дизайнеры «ABBYY» выложили все элементы мозаики в ряд, не соединяя их между собой. Назовем набором несколько подряд лежащих элементов мозаики в этом ряду. Они выбрали несколько наборов элементов, которые хотят оставить для создания инсталляции. Для каждого такого набора им нужно выяснить, есть ли в нем негармоничная пара элементов. Требуется написать программу, которая для различных наборов подряд лежащих элементов мозаики определит номера элементов, образующих негармоничную пару, или сообщит, что такой пары нет.
В первой строке входного файла записано одно число N – количество элементов, из которых состоит мозаика (2 ≤ N ≤ 100 000). В следующих N строках записаны по два целых числа Ai и Bi , задающих длину и ширину i-го элемента мозаики соответственно (1 ≤ Ai, Bi ≤ 109, 1 ≤ i ≤ N). В (N + 2)-й строке записано одно целое число K – количество наборов, в каждом из которых нужно определить номера двух негармоничных элементов (1 ≤ K ≤ 100 000). В следующих K строках записаны пары целых чисел N1 и N2 – номера первого и последнего элементов набора соответственно, в котором необходимо найти два негармоничных элемента мозаики (1 ≤ \(N_1\) < \(N_2\) ≤ N).
Выходной файл должен содержать K строк, каждая из которых содержит два разделённых пробелом числа – номера элементов мозаики, образующих негармоничную пару в соответствующем наборе. Если решений несколько, можно вывести любое из них. Если в наборе негармоничная пара отсутствует, требуется вывести в соответствующей строке 0 0.
Данная задача содержит четыре подзадачи. Для оценки каждой подзадачи используется своя группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы успешно пройдены.
4 2 2 1 2 1 3 2 3 2 2 3 2 4
0 0 4 2
Дан массив. Надо научиться обрабатывать два типа запросов.
* 1 L R - перевернуть отрезок \([L,\,R]\)
* 2 L R - найти минимум на отрезке \([L,\,R]\)
Первая строка файла содержит два числа \(n\), \(m\). (\(1 \le n,m \le 10^5\)) Во второй строке находится \(n\) чисел \(a_i\) (\(1 \le a_i \le 10^9\)) — исходный массив. Остальные \(m\) строк содержат запросы, в формате описанном в условии. Для чисел \(L\), \(R\) выполняется ограничение (\(1 \le L \le R \le n\)).
На каждый запрос типа 2, во входной файл выведите ответ на него, в отдельной строке.
10 7 5 3 2 3 12 6 7 5 10 12 2 4 9 1 4 6 2 1 8 1 1 8 1 8 9 2 1 7 2 3 6
3 2 2 2
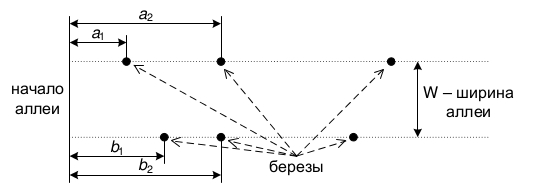
На краю деревни растет старая березовая аллея. Аллея имеет форму прямой полосы шириной \(W\) метров. Вдоль левой стороны аллеи растет \(N\) берез, а вдоль правой — \(M\) берез, при этом \(i\)-я береза с левой стороны аллеи находится на расстоянии \(a_i\) метров от начала аллеи, а \(j\)-я береза с правой стороны — на расстоянии \(b_j\) метров от начала аллеи.
Отдыхая в деревне прошедшим летом, один юный информатик обнаружил, что кору берез стали грызть зайцы. Чтобы защитить деревья от зайцев, мальчик решил окружить березы красной лентой (зайцы не любят красный цвет и не станут заходить на огражденную лентой территорию. К сожалению, в его распоряжении оказалась только лента длиной \(L\) метров, которую, к тому же, нельзя было разрезать. Единственное, что можно было делать в этом случае — окружить этой лентой как можно больше берез. При этом, чтобы сохранить аллею, необходимо окружить на каждой стороне аллеи хотя бы одну березу.
Требуется написать программу, которая по заданной длине ленты, ширине аллеи и положению берез на ней определяет максимальное число берез, которое можно окружить этой лентой. Считается, что березы представляются точками, толщиной берез и шириной ленты следует пренебречь.
Первая строка входного файла содержит два разделенных пробелом целых числа: длину ленты \(L\) и ширину аллеи \(W\) (\(1 \leq L \leq 2 \times 10^5\), \(1 \leq W \leq 10^4\)).
Вторая и третья строки описывают березы вдоль левой стороны аллеи. Вторая строка содержит число \(N\) — количество берез (\(1 \leq N \leq 2000\)), а третья строка содержит \(N\) различных целых чисел \(a_1\), \(a_2\), …, \(a_N\) (\(0 \leq a_i \leq 10^5\)), заданных по возрастанию.
Четвертая и пятая строки описывают березы вдоль правой стороны аллеи. Четвертая строка содержит число \(M\) — количество берез (\(1 \leq M \leq 2000\)), а пятая строка содержит \(M\) различных целых чисел \(b_1\), \(b_2\), …, \(b_M\) (\(0 \leq b_i ≤ 10^5\)), заданных по возрастанию.
Выходной файл должен содержать одно целое число: максимальное количество берез, которое можно оградить заданной лентой.
Гарантируется, что если максимальное число берез, которое можно оградить лентой длины L, равно X, то нет способа оградить (X + 1) березу лентой длины (L + \(10^{-5}\)).
Правильные решения для тестов, в которых 1 ≤ N + M ≤ 50, будут оцениваться из 30 баллов.
Правильные решения для тестов, в которых 1 ≤ N + M ≤ 500, будут оцениваться из 60 баллов.
18 4 3 0 3 6 4 0 3 6 10
5
5 3 1 0 1 0
0