| Ограничение по времени, сек | 0.75 |
| Ограничение по памяти, мегабайт | 256 |
Министерство обороны Флатландии планирует построить новый военный полигон. Полигон должен иметь форму круга.
Поскольку генералы в министерстве волнуются о секретности проводимых на полигоне испытаний, он должен быть надежно защищен. Флатландия защищена сверху несколькими специальными силовыми щитами, каждый из них имеет форму прямоугольника со сторонами, параллельными осям координат. Генералы хотят выбрать такое место для полигона, где он был бы полностью защищен хотя бы двумя конкретными силовыми щитами (недостаточно, чтобы каждая точка просто была защищена хотя бы двумя щитами, должно быть два щита, каждый из которых защищает полигон полностью).
Конечно, генералы хотят построить полигон максимального возможного размера. Помогите им выбрать такое место для полигона, чтобы он имел максимальный возможный радиус.
Первая строка входного файла содержит число \(N\) — количество силовых щитов. Каждая из следующих N строк описывает силовой щит (\(1 \leq N \leq 200000\)). Описание представляет собой четверку координат: \(x_{min}\), \(y_{min}\), \(x_{max}\), \(y_{max}\). Все координаты целые и не превышают 100000 по абсолютной величине.
Выведите три вещественных числа — координаты центра полигона и его радиус. Все числа следует выводить ровно с одним знаком после десятичной точки.
Если построить полигон невозможно, выведите “Impossible” на первой строке выходного файла.
4 0 0 2 3 1 -1 4 1 1 1 4 4 2 0 5 5
3.0 2.0 1.0
1 0 0 1 1
Impossible
2 0 0 3 3 0 0 3 3
1.5 1.5 1.5
История Татаро-монгольского ханства богата на правителей. Каждый из N правителей принадлежал к одной из двух династий, причём власть часто переходила от одной династии к другой. Каждое восхождение правителя на престол отмечалось праздником, проводимым 26 марта. В летописях зафиксированы годы проведения этих праздников, причем известно, что правители первой династии устраивали для народа праздник кумыса, а второй — праздник мёда.
На конференции по истории Татаро-монгольского ханства каждый из S учёных предложил свою версию толкования летописи. А именно, i-й историк утверждал, что от каждого праздника кумыса до следующего праздника кумыса проходило не менее KLi лет, но не более KRi лет, в то время как от каждого праздника мёда до следующего праздника мёда проходило не менее MLi лет, но не более MRi лет.
Каждой предложенной версии может соответствовать несколько распределений правителей по династиям. Ученые договорились считать показателем сомнительности распределения число переходов власти к представителю той же самой династии.
Требуется написать программу, которая найдёт распределение, соответствующее хотя бы одной из версий и имеющее наименьший показатель сомнительности, а также версию, которой оно соответствует.
В первой строке входного файла записано число N (2 ≤ N ≤ 200 000) — количество праздников в летописи. Следующая строка содержит целые числа X1, X2, ..., XN (1 ≤ X1 ≤ X2 ≤ ... ≤ XN ≤ 109) — годы проведения праздников.
В третьей строке записано число учёных S (1 ≤ S ≤ 50). В каждой из последующих S строк записаны четыре натуральных числа KLi, KRi, MLi, MRi (1 ≤ KLi ≤ KRi ≤ 109), (1 ≤ MLi ≤ MRi ≤ 109).
Первая строка выходного файла должна содержать числа P и Q, где P — номер учёного, версии которого соответствует распределение с наименьшим показателем сомнительности, а Q — показатель сомнительности этого распределения.
Вторая строка должна состоять из N цифр 1 и 2, записанных без пробелов, означающих приход к власти представителя первой или второй династии соответственно. Если существует несколько решений с наименьшим показателем сомнительности Q, выведите любое из них.
В случае, если ни в одной из версий учёных не существует способа распределения периодов правления между династиями так, чтобы не нарушались ограничения на промежутки времени между праздниками, выходной файл должен содержать единственное число 0.
Данная задача содержит шесть подзадач. Для оценки каждой подзадачи используется своя группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы пройдены.
3 1 2 3 1 1 1 1 1
1 1 211
4 1 6 9 13 2 1 2 2 3 6 7 3 3
0
5 3 6 8 9 10 2 2 3 1 1 1 4 1 10
2 0 21212
Постановка задачи о {Наименьшем общем предке} такова: дано дерево T с выделенным корнем и две вершины u и v, lca(u, v) - вершина с максимальной глубиной, которая является предком и u, и v. Например, в картинке внизу lca(8, 7) - вершина 3.
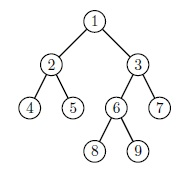
С помощью операции chroot(u) мы можем менять корень дерева, достаточно отметить u, как новый корень, и направить ребра вдоль пути от корня. Наименьшие общие предки вершин поменяются соответствующе. Например, если мы сделаем chroot(6) на картинке сверху, lca(8, 7) станет вершина 6. Получившееся дерево изображено снизу.
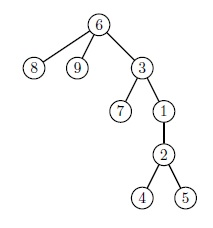
Вам дано дерево T. Изначально корень этого дерева - вершина 1. Напишите программу, которая поддерживает эти две операции: lca(u, v) и chroot(u).
Входной файл состоит из нескольких тестов.
Первая строка каждого теста содержит натуральное число n — количество вершин в дереве (1 ≤ n ≤ 100 000). Следующие n - 1 строки содержат по 2 натуральных числа и описывают ребра дерева. Далее идет строка с единственным натуральным числом m — число операций —. Следующие m строк содержат операции. Строка "? u v" означает операцию lca(u, v), a строка "! u" - chroot(u). Последняя строка содержит число 0.
Сумма n для всех тестов не превосходит 100 000. Сумма m для всех тестов не превосходит 200 000.
Для каждой операции "? u v" выведите значение lca(u, v). Числа разделяйте переводами строк.
Система тестов состоит из двух групп:
Первая группа состоит из тестов, для которых выполняется ограничение \(n \le 100\), \(m \le 10000\). За прохождение всех тестов группы ставится 55 баллов.
Вторая группа стоит из тестов, в которых нет дополнительных ограничений. За прохождение тестов этой группы и всех предыдущих тестов ставится дополнительно 45 баллов.
9 1 2 1 3 2 4 2 5 3 6 3 7 6 8 6 9 10 ? 4 5 ? 5 6 ? 8 7 ! 6 ? 8 7 ? 4 5 ? 4 7 ? 5 9 ! 2 ? 4 3 0
2 1 3 6 2 3 6 2
Задано подвешенное дерево, содержащее n (1 ≤ n ≤ 100 000) вершин, пронумерованных от 0 до n - 1. Требуется ответить на m (1 ≤ m ≤ 10 000 000) запросов о наименьшем общем предке для пары вершин. Запросы генерируются следующим образом. Заданы числа a1, a2 и числа x, y и z. Числа a3, ..., a2m генерируются следующим образом: ai =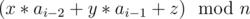 
. Первый запрос имеет вид {a1, a2}. Если ответ на (i - 1)-й запрос равен v, то i-й запрос имеет вид {
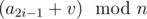, a2i}.
Первая строка содержит два числа: n и m. Корень дерева имеет номер 0. Вторая строка содержит n - 1 целых чисел, i-е из этих чисел равно номеру родителя вершины i. Третья строка содержит число содержит два целых числа в диапазоне от 0 до n - 1: a1 и a2. Четвертая строка содержит три целых числа: x, y и z, эти числа неотрицательны и не превосходят 109.
Выведите в выходной файл сумму номеров вершин — ответов на все запросы.
3 2 0 1 2 1 1 1 0
2
Последовательность ДНК любого живого существа в Берляндии представима в виде непустой строки из маленьких латинских букв. Берляндские ученые выяснили, что эволюции всех существ происходят поэтапно. На одном этапе ровно один некоторый символ последовательности ДНК заменяется ровно на два других. При этом всего бывает n допустимых замен. Замена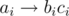 
означает, что можно заменить один любой символ ai на пару символов bici. Каждая замена могла произойти неограниченное число раз.
Говорят, что два существа, имеющие последовательности ДНК s1 и s2, могут иметь общего предка, если существует такая последовательноcть ДНК s3, что из нее в процессе эволюции могут быть получены s1 и s2, возможно за разное число этапов. По заданным s1 и s2 требуется определить, могут ли существа, имеющие такие последовательности ДНК, иметь общего предка. В случае положительного ответа требуется найти длину кратчайшей последовательноcти ДНК общего предка.
В первой строке записана непустая последовательность ДНК s1, во второй строке записана непустая последовательность ДНК s2. Длины этих строк не превосходят 50, строки содержат только маленькие латинские буквы. В третьей строке записано целое число n(0 ≤ n ≤ 50) допустимых замен. Далее следует n строк, каждая из которых описывает очередную замену в формате 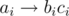. Символы ai, bi, и ci — маленькие латинские буквы. Строки s1 и s2 могут совпадать, список замен может содержать одинаковые замены.
Если s1 и s2 не могут иметь общего предка, выведите -1. Иначе выведите длину кратчайшей последовательности s3, из которой могли быть получены s1 и s2.
ababa aba 2 c->ba c->cc
2
ababa aba 7 c->ba c->cc e->ab z->ea b->ba d->dd d->ab
1