Отсортируйте данный массив. Используйте пирамидальную сортировку.
Первая строка входных данных содержит количество элементов в массиве N, N ≤ 105. Далее задаются N целых чисел, не превосходящих по абсолютной величине 109.
Выведите эти числа в порядке неубывания.
В этой задаче вам необходимо организовать структуру данных Heap для хранения целых чисел, над которой определены следующие операции:
a) Insert(k) – добавить в Heap число k (1 ≤ k ≤ 1000000) ;
b) Extract достать из Heap наибольшее число (удалив его при этом).
В первой строке содержится количество команд N (1 ≤ N ≤ 100000), далее следуют N команд, каждая в своей строке. Команда может иметь формат: “0 <число>” или “1”, обозначающий, соответственно, операции Insert(<число>) и Extract. Гарантируется, что при выполенении команды Extract в структуре находится по крайней мере один элемент.
Для каждой команды извлечения необходимо отдельной строкой вывести число, полученное при выполнении команды Extract.
2 0 10000 1
10000
Рассмотрим последовательность целых чисел длины N. По ней с шагом 1 двигается “окно” длины K, то есть сначала в “окне” видно первые K чисел, на следующем шаге в “окне” уже будут находиться K чисел, начиная со второго, и так далее до конца последовательности. Требуется для каждого положения “окна” определить минимум в нём.
В первой строке входных данных содержатся два числа N и K (1 ≤ N ≤ 150000, 1 ≤ K ≤ 10000, K ≤ N) – длины последовательности и “окна”, соответственно. На следующей строке находятся N чисел – сама последовательность.
Выходые данные должны содержать N − K + 1 строк – минимумы для каждого положения “окна”.
7 3 1 3 2 4 5 3 1
1 2 2 3 1
Реализуйте бинарное дерево поиска для целых чисел. Программа получает на вход последовательность целых чисел и строит из них дерево. Элементы в деревья добавляются в соответствии с результатом поиска их места. Если элемент уже существует в дереве, добавлять его не надо. Балансировка дерева не производится.
На вход программа получает последовательность натуральных чисел. Последовательность завершается числом 0, которое означает конец ввода, и добавлять его в дерево не надо.
Выведите единственное число – количество уровней получившегося дерева.
Пример соответствует следующему дереву:
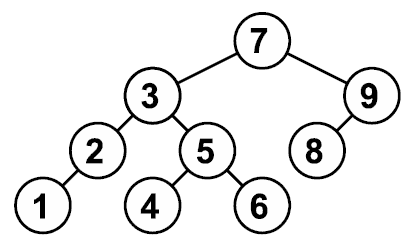
7 3 2 1 9 5 4 6 8 0
4
Подсчитайте количество элементов в получившемся дереве и выведите это количество.
Вводится последовательность целых чисел, оканчивающаяся нулем. Сам ноль в последовательность не входит.
Выведите ответ на задачу.
7 3 2 1 9 5 4 6 8 0
9