Двоичное дерево поиска(24 задач)
Дерево отрезков, RSQ, RMQ(90 задач)
Бор(14 задач)
Дерево Фенвика(6 задач)
Декартово дерево(10 задач)
Компания « Rapid City Dynamics » знаменита её роботами-собаками, роботами-гепардами и даже человекоподобными роботами. Но большие проекты требуют больших денег, так что компания решила создать что-то простое, но популярное (и более востребованное). Так что компания разрабатывает нового робота « Rat-O-Matic », и вы, как работник « Rapid City Dynamics », принимаете участие в этом.
Робот выглядит как механическая крыса, которая может двигаться и генерировать мелодию, наступая на специальные рамки. Плоскость бесконечна во все стороны, и на ней задана декартова система координат.
Есть ровно n рамок. Каждая рамка задана тремя числами: x , y и r . Она задаёт территорию, ограниченую между двух квадратов со сторонами параллельным осям координат и центрами в точке ( x , y ): радиус первого квадрата r , а второго — 2· r . Радиус квадрата — это расстояние между его центром и стороной. Ко всему прочему, каждой рамке соответствует своя нота. Сейчас есть только 3 возможных ноты, обозначим их как « r », « a » и « t ».
Гарантируется, что никакие две рамки не касаются и не пересекаются.
Вы можете взаимодействовать с роботом, вбивая номер рамки на специальной клавиатуре (рамки пронумерованы начиная с 1 ). Изначально, крыса находится снаружи всех рамок. Благодаря патентованной системе навигации, робот выбирает путь до рамки, который пересекает минимальное количество рамок. Когда крыса наступает на рамку в первый раз, соответствующая нота добавляется в мелодию. Робот останавливается после того, как наступит на нужную рамку.
Известно, что людям нравятся похожие мелодии. В вашей базе данных имеются m мелодий. Каждая мелодия задаётся строкой из символов, которая задаёт ноты. Мелодия, сгенерированная крысой, содержится в мелодии из базы данных, если она содержится в ней в качестве подстроки. Популярность сгенерированной мелодии - это число мелодий в базе данных, которые содержат её. Одинаковые мелодии из базы данных должны быть учтены несколько раз.
В попытке создания самого классного расположения рамок, вы совершили q экспериментов. Эксперименты бывают трёх типов:
Твоя задача — провести эти эксперименты, используя только свой компьютер!
В первой строке содержится натуральное число n — количество рамок ( 1 ≤ n ≤ 2·10 5 ).
В следующих
n
строках описаны рамки,
i
-я из них содержит три натуральных числа
x
i
,
y
i
,
r
i
и символ
c
i
, разделённые пробелами (
- 10
8
≤
x
i
,
y
i
≤ 10
8
,
1 ≤
r
i
≤ 10
8
, и
c
i
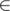 {«
r
», «
a
», «
t
»} — координаты центра рамки, радиус внутреннего квадрата и её нота, соответственно.
{«
r
», «
a
», «
t
»} — координаты центра рамки, радиус внутреннего квадрата и её нота, соответственно.
Следующая строка содержит натуральное число m — количество мелодий в базе ( 1 ≤ m ≤ 2·10 5 ).
Следующие m строк содержат непустые строки из букв « r », « a » или « t », которые задают мелодии. Суммарная длина всех строк не превосходит 2·10 5 .
Следующая строка содержит натуральное число q — количество экспериментов ( 1 ≤ q ≤ 2·10 5 ).
Следующие q строк описывают эксперименты, j -я из них содержит символ t j (« - », « + » или « ? ») и натуральное число x j отделённое пробелом. Символ задаёт тип эксперимента (« - » — 1, « + » — 2 и « ? » — 3), а число обозначает номер рамки.
Гарантируется, что есть хотя бы один эксперимент третьего типа.
Для каждого эксперимента третьего типа, выведите одно число — популярность получившейся мелодии.
10 баллов — (1 ≤ n, m, q ≤ 100, суммарная длина строк не превосходит 100, тесты 2-6) .
10 баллов — ( 1 ≤ n ≤ 4 000, 1 ≤ m, q ≤ 100, суммарная длина строк не превосходит 100, тесты 7-9) .
10 баллов — ( 1 ≤ n, q ≤ 100, 1 ≤ m ≤ 200 000 , суммарная длина строк не превосходит 200 000, тесты 10-13) .
10 баллов — ( 1 ≤ n ≤ 4 000, 1 ≤ m ≤ 200 000, 1 ≤ q ≤ 100, суммарная длина строк не превосходит 200 000, тесты 14-16) .
10 баллов — ( 1 ≤ n ≤ 200 000, 1 ≤ m, q ≤ 100, суммарная длина строк не превосходит 100, тесты 17-19) .
15 баллов — ( 1 ≤ n, q ≤ 200 000, 1 ≤ m ≤ 100, суммарная длина строк не превосходит 100, тесты 20-23) .
35 баллов — полные ограничения, тесты 24-57.
3 3 3 4 r 2 4 1 a 14 4 1 t 3 rat rara aaa 6 ? 3 ? 2 - 1 ? 2 + 1 ? 2
1 2 3 2
В Флатландии идет пора реформ. Недавно была проведена реформа дорог, так что теперь по дорогам страны из любого города можно добраться в любой другой, причем только одним способом. Также была проведена реформа волшебников, так что в каждом городе остался ровно один волшебник. Теперь же началась реформа почтовой системы.
Недавно образованное почтовое агентство «Экс-Федя» предлагает уникальную услугу — коллективную посылку. Эта услуга позволяет отправлять посылки жителям всех городов на каком-либо пути по цене обычной посылки. Удивительно, но пользоваться такой услугой стали только волшебники Флатландии, которые стали в большом количестве отправлять друг другу магические кактусы. Агентство столкнулось с непредвиденной проблемой: как известно, все волшебники живут в башнях и мало того, что не строят в них лестницы, так еще время от времени меняют их высоту. Поэтому, чтобы доставить посылку волшебнику, который живет в башне высотой h , курьеру агентства требуется иметь с собой не менее h метров веревки.
Вам поручено руководить отделом логистики — по имеющимся данным о высотах башен и об их изменениях вам нужно определять минимальную длину веревки, которую нужно выдать курьеру, который доставляет посылки между городами i и j .
Первая строка входного файла содержит число n — количество городов в Флатландии ( 1 ≤ n ≤ 50 000 ). Во второй строке находится n положительных чисел, не превосходящих 10 5 — высоты башен в городах. В следующих n - 1 строках содержится по два числа u i и v i — описание i -й дороги, 1 ≤ u i , v i ≤ n , u i ≠ v i . В следующий строке содержится число k — количество запросов ( 1 ≤ k ≤ 100 000 ). В следующих k строках содержатся описания запросов в следующем формате:
Для каждого запроса доставки посылок выведите минимальную длину веревки, которую необходимо выдать курьеру.
20 баллов — ( 1 ≤ n, k ≤ 100) .
30 баллов — каждый город соединен дорогами не более чем с двумя другими.
50 баллов — полные ограничения.
3 1 2 3 1 3 2 3 5 ? 1 2 ! 1 5 ? 2 3 ! 3 2 ? 1 2
3 3 5
1 100 5 ! 1 1 ? 1 1 ! 1 1000 ? 1 1 ! 1 1
1 1000
|
Я на выборы никогда не ходил, но в этот раз точно пойду за Зигги голосовать. Кандидат от народа!
Вдохновившись трудами греческих философов, Спортакус решил избрать главу правительства в Лентяево. Поскольку греческие философы убедили Спортакуса, что демократия является лучшим видом государственного устройства, он решил провести выборы. Для этого он открыл n избирательных участков, пронумерованных от 1 до n . Известно, что на участке с номером i проголосовали a i жителей Лентяево.
После окончания выборов Спортакус решил подвести некоторую статистику явки на выборах. Спортакус знает множество разных статитстических величин, но наиболее показательной он считает k -ю порядковую статистику, поэтому для некоторых регионов и некоторых значений k Спортакус хочет узнать значение k -й порядковой статистики явок на участках данного региона.
Опишем действия Спортакуса более формально. Регионом с границами l и r Спортакус называет множество избиртельных участков, чьи номера лежат на промежутке от l до r включительно. k -й порядковой статистикой массива чисел супергерой называет число, которое бы находилось на k -й позиции в этом массиве, если бы он был упорядочен по возрастанию.
Стефани огорчает, что явка на выборах не соотетствует её ожиданиям, поэтому она решила слегка изменить значения явок на некоторых участках так, чтобы выборы казались более успешными. Для этого она выбирает четыре числа l , r , x и y и на всех избирательных участках региона с границами l и r , на которых явка равна x меняет протокол, после чего явка на этих участках становится равной y .
Напишите программу, отвечающую на запросы Спортакуса с учётом изменений, которые делает Стефани.
В первой строке содержатся два целых числа n и m ( 1 ≤ n , m ≤ 100 000 ) — количество избирательных участков и количество событий.
Во второй строке содержатся n целых чисел ( 1 ≤ a i ≤ n ) — количество людей, проголосовавших на участке с номером i .
В следующих m строках содержатся описания событий. Каждое событие задано в одном из двух форматов.
1 l r x y ( 1 ≤ l ≤ r ≤ n , 1 ≤ x , y ≤ n ) обозначает, что Стефани на всех участках региона с границами l и r и явкой x установила явку равной y .
2 l r k ( 1 ≤ l ≤ r ≤ n , 1 ≤ k ≤ r - l + 1 ) обозначает, что Спортакуса интересует значение k -й порядковой статистики явок на участках в регионе с границами l и r .
Для каждого вопроса Спортакуса выведите ответ на него.
Группа 1 (10 баллов) 1 ≤ n , m ≤ 100 . Для прохождения этой подгруппы требуется прохождение тестов из условия.
Группа 2 (10 баллов) 1 ≤ n ≤ 5000, 1 ≤ m ≤ 100 000 , нет запросов первого типа. Для прохождения этой подгруппы требуется прохождение тестов из условия.
Группа 3 (10 баллов) 1 ≤ n , m ≤ 100 000 , нет запросов первого типа. Для прохождения этой подгруппы требуется прохождение группы 2.
Группа 4 (20 баллов) 1 ≤ n , m ≤ 100 000 , в запросах первого типа l = r . Для прохождения этой подгруппы требуется прохождение группы 3.
Группа 5 (50 баллов) Без дополнительных ограничений. Для прохождения этой подгруппы требуется прохождение всех предыдущих групп.
3 3 2 3 3 2 1 3 1 1 1 3 3 1 2 1 3 2
2 1
В один прекрасный день маленький Дональд решил вымыть N своих чистых белых простыней. После мытья он положил их на землю во дворе, чтобы их высушить. Дональд помещал простыни так, чтобы никакие две простыни не касались ни сторонами, ни углами, и чтобы их стороны не пересекалась, но возможно, что он разместил меньшие простыни поверх более крупных или что простыня полностью закрывает какие-то другие простыни. Сделав это, Дональд лег спать.
Друг Дональда Ким как-то узнал о том, что Дональд сушит простыни и решил пообщаться с ним. Он нашел пейнтбольный пистолет своего отца на чердаке. Наряду с пистолетом у него было несколько пейнтбольных мячей, каждый из них имел свой цвет (не обязательно уникальный). Как только Дональд заснул, Ким вошёл во двор к Дональду и начал стрелять пр простыням из пейнтбольного пистолета. Простыни Дональда очень тонкие, поэтому, когда Ким попадает в какую-то простыню, она пропускает краску дальше, на простыню ниже (и та тоже, и так происходит, пока не закончатся простыни и краска не попадет на землю). После того, как Ким использовал все шары, он с радостью покинул двор Дональда. Дональд был очень расстроен, увидев, что случилось с его простынями. Дональд очень заинтересован в правильных данных о преступлении Кима, но он в шоке и не способен думать, поэтому просит вас сказать ему количество цветов на каждой простыне.
Мы можем представлять двор Дональда как бесконечную систему координат, а простыни - как прямоугольники, параллельные осям координат. Выстрелы Кима могут быть представлены как точки в этой системе.
Когда-то в детстве дедушка рассказал Киму, что снаряд никогда не попадает в одну воронку дважды, так что координаты всех выстрелов попарно различны.
Первая строка ввода содержит два числа - количество простынь N ( 1 ≤ N ≤ 80000 ), и количество шаров M ( 1 ≤ M ≤ 80 000 ).
i -я из следующих N строк содержит четыре числа: координаты нижнего левого угла A i , B i ( 1 ≤ A i , B i ≤ 10 9 ) и верхнего правого угла C i , D i , ( 1 ≤ C i , D i ≤ 10 9 ) i -й простыни.
j -я из следующих M строк содержит три числа, где X j , Y j ( 1 ≤ X j , Y j ≤ 10 9 ) - координаты j -го выстрела Кима и K j ( 1 ≤ K j ≤ 10 9 ) - цвет j -го пейнтбольного шара.
i -я из N выходных строк должна содержать количество цветов на i -м листе.
Тесты к данной задаче состоят из трёх групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов необходимых групп.

2 2 1 1 3 3 5 6 10 10 3 3 1 5 1 2
1 0
3 3 1 1 7 7 2 2 6 6 3 3 5 5 4 4 1 2 6 2 4 7 3
3 2 1
1 3 1 1 7 7 2 6 2 4 7 3 4 4 1
3
Вы когда-нибудь мечтали стать главным героем компьютерной игры? Главный герой этой истории, Бранимир, мечтает сейчас именно об этом.
Мир в мечте Бранимира состоит из N небоскребов, пронумерованных слева направо. Для i -го небоскреба, известна его высота H i и количество золотых монет G i на крыше этого небоскреба. Игра начинается с прыжка на любой из небоскребов и состоит из нескольких ходов. На каждом ходу Бранимир может прыгнуть на любой небоскрёб, находящийся справа от него, но так, чтобы высота нового небоскрёба была не меньше того небоскрёба, на котором сейчас сидит Бранимир. Оказавшись на крыше небоскреба, Бранимир собирает все золотые монеты на ней. Бранимир может закончить игру после любого количества шагов (возможно, нулевого), но он должен собрать не менее K золотых монет, чтобы перейти на следующий уровень.
Бранимир хочет узнать, сколько существует способов сыграть в эту игру так, чтобы перейти на следующий уровень. Две игры называются разными, если существует небоскреб который был посещен в одной игре, но не был посещён в другой.
Первая строка содержит 2 натуральных числа N и K ( 1 ≤ N ≤ 40 , 1 ≤ K ≤ 4·10 10 ) — число небоскрёбов и количество монет, которые надо набрать соответственно.
Следующие N строк содержат информацию о небоскрёбах. В i -й строке даны 2 числа H i и G i ( 1 ≤ H i , G i , ≤ 10 9 ) — высота и количество монет на i -м небоскрёбе.
В единственной строке вывода выведите число возможных игр, в которых Бранимир сможет пройти на следующий уровень.
Решение, корректно работающее при n ≤ 20 будет оцениваться в 40 баллов.
4 6 2 1 6 3 7 2 5 6
3
2 7 4 6 3 5
0
4 15 5 5 5 12 6 10 2 1
4