Возвращаясь из школы домой, Петя каждый раз обращал внимание на надпись на заборе «1 + 1 = 10» и удивлялся очевидной его неправоте. Но однажды его осенило, что это равенство верное, если рассматривать его в двоичной системе счисления. Его настолько поразила эта идея, что он решил непременно придумать свои три числа так, чтобы сумма первых двух была равна третьему в некоторой системе счисления.

Теперь он перебирает тройки чисел, которые, на его взгляд, достойны находиться на заборе. Петя выбирает числа A, B, C, записывающиеся десятичными цифрами, и дальше пытается найти основание системы счисления K, в которой равенство A + B = C оказалось бы верным. Петя рассматривает системы счисления с основанием от 2 до бесконечности.

Поскольку проверка каждой тройки — занятие трудоемкое, в помощь Пете необходимо написать программу, облегчающую расчеты.

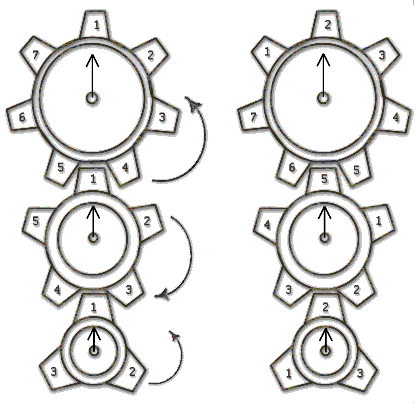На каждой из трех осей установлено по одной вращающейся шестеренке и неподвижной стрелке. Шестеренки соединены последовательно. На первой шестеренке n зубцов, на второй — m, на третьей — k. На каждом зубце первой, второй и третьей шестеренок по часовой стрелке написаны в порядке возрастания числа от 1 до n, от 1 до m и от 1 до k соответственно. Стрелки зафиксировали таким образом, что когда стрелка первой оси указывает на число, стрелки двух других осей также указывают на числа. Витя записывает три числа (a₁,a₂,a₃), на которые указывают стрелки. После этого он поворачивает первую шестеренку на угол 360°/n против часовой стрелки, чтобы напротив стрелки на первой оси оказался следующий (по часовой стрелке) зубец. При этом вторая шестеренка поворачивается на угол 360°/m по часовой стрелке (размеры зубцов у шестеренок одинаковые, поэтому размеры самих шестеренок разные, чтобы на границе шестеренок равномерно уложилось разное число одинаковых по размеру зубцов), а третья шестеренка поворачивается на угол 360°/k против часовой стрелки. Витя опять записывает три числа, на которые указывают стрелки.

Поступая и далее таким образом, Витя заметил, что после некоторого количества таких действий стрелки показывают на три первоначальных числа.

Теперь его очень интересует, как по двум данным тройкам чисел определить, принадлежат ли они к одной последовательности, то есть можно ли некоторым количеством поворотов перейти от первой тройки ко второй. Он попросил вас написать программу, которая отвечает на этот вопрос.

>Во время исследований, посвященных появлению жизни на планете Олимпия, учеными было сделано несколько сенсационных открытий:

1. Все живые организмы планеты происходят от бактерии Bitozoria Programulis.
2. Эволюция происходила шаг за шагом (по предположению ученых – во время изменения климата на планете).
3. На каждом шаге эволюции из каждого вида образовывались ровно два подвида, а предыдущий вид исчезал.
4. Если считать появление бактерии Bitozoria Programulis первым шагом эволюции, то существующие сейчас живые организмы находятся на N-ом шаге.

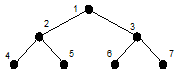
Чтобы не придумывать названия во время исследований, ученые пронумеровали все виды организмов, которые когда-либо существовали на планете. Для этого они нарисовали дерево эволюции с корнем Bitozoria Programulis, которая получила номер 1. Далее нумеровали виды каждого шага эволюции слева направо. Таким образом непосредственные подвиды Bitozoria Programulis получили номера 2 и 3. Следующими были занумерованы виды третьего шага эволюции – подвиды вида 2 получили номера 4 и 5, а вида 3 – номера 6 и 7, и т.д.

Напишите программу, которая по номерам двух видов вычислит номер вида их ближайшего общего предка в дереве эволюции.

Во время экперимента Накодиллы было случайно получено сообщение инопланетян, содержащее формулу вида A + B = C.

Общественности стало интересно, какую же систему счисления используют инопланетяне. Так как внеземная цивилизация была достаточно развита, чтобы отправить межпланетное сообщение, Накодилла предположил, что основание системы счисления довольно мало. Требуется написать программу, которая находит минимальное основание системы счисления, при котором данное равенство выполняется.

Даны две сцепленные шестеренки. У одной шестеренки N зубцов, у другой – K. Требуется найти, какое минимальное число поворотов на один зубчик требуется сделать, чтобы шестеренки вернулись в исходное состояние.