Фирма, в которой всё ещё работает ваш друг, решила установить в своих маршрутках автоматы по продаже чая и кофе, чтобы во время поездок и, особенно, во время ожидания в пробках, пассажиры могли с толком провести время.

Стоимость стакана чая и кофе в автомате предполагается установить равной пяти рублям. Автоматы будут принимать монеты по 5 и 10 рублей, а также купюры в 10, 50 и 100 рублей. Когда пассажиру надо выдавать сдачу (т.е. когда пассажир бросил в автомат десятирублёвую монету или 10-, 50- или 100- рублёвую купюру), автомат выдаёт сдачу пятирублёвыми монетами; если же пассажир бросил в автомат пятирублёвую монету, то автомат её сохраняет и может использовать для сдачи следующим пассажирам. Ясно, что, чтобы обеспечить возможность выдачи сдачи всем покупателям, может потребоваться изначально загрузить в автомат некоторое количество пятирублёвых монет. Сейчас на маршрутках фирмы проходят испытания с целью определить минимальное количество монет, которые надо загрузить в автомат перед выездом маршрутки в рейс. Вам дан протокол одного из таких испытаний: известен порядок, в котором пассажиры оплачивали свои покупки различными монетами и купюрами. Определите, какое минимальное количество пятирублёвых монет должно было изначально находиться в автомате, чтобы всем пассажирам хватило сдачи.

Большое количество соревнований по разным видам спорта проводится по так называемой "олимпийской системе". В простейшем варианте она состоит в следующем. В турнире участвуют N = 2^k игроков. Они получают номера от 1 до N, и в первом круге игрок 1 играет с игроком 2, игрок 3 с игроком 4 и т. д., игрок (N - 1) — с игроком N. Проигравшие в каждой паре выбывают из соревнований, а победители проходят во второй круг. Там победитель первой пары (т. е. игрок 1 или игрок 2) играет с победителем второй пары и т. д. Таким образом, в первом круге участвуют N = 2^k игроков, во втором круге — 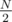= 2^k - 1 и т. д., в финале участвуют два игрока.

Серьезной проблемой является то, что некоторые сильные игроки могут встретиться между собой уже в одном из первых кругов, в результате чего некоторые сильные участники могут рано выбыть из борьбы, в то время как другие, менее сильные участники, могут пройти намного выше, если им повезет с соперниками. Для борьбы с этим эффектом применяется так называемый “рассев” игроков, когда начальная нумерация участников не является полностью случайной, и вероятность “везения”/”невезения” с соперниками резко уменьшается.

В этой задаче вам нужно будет написать программу, находящую в некотором смысле оптимальный “рассев” игроков. Для этого рассмотрим следующую модель. Предположим, что участников можно упорядочить по силе так, что более сильный игрок всегда будет выигрывать у более слабого. В таком случае по изначальному “рассеву” игроков дальнейший ход соревнований будет однозначно определен. Тогда в качестве критерия оптимальности рассева” можно потребовать выполнение следующих условий: в финале играют двое сильнейших игроков, в полуфиналах играют четверо сильнейших игроков, и т. д.: в каждом круге играют только сильнейшие игроки (т. е. если в каком-то круге m мест, то в этом круге должны участвовать m сильнейших игроков). Вам дано N. Найдите любой оптимальный рассев N игроков.

Зачет проводится в аудитории, в которой стоит один большой круглый стол, за которым ровно N мест; студентов в группе тоже ровно N. За время семестра преподаватель успел выделить несколько пар студентов, которые, по его мнению, могут списывать друг у друга, при этом каждый студент входит не более чем в одну такую пару. Теперь он хочет придумать такую рассадку для студентов, чтобы они все решали задачи самостоятельно.

Преподаватель считает, что списывать сложнее всего, если тот, у кого списывают, находится на расстоянии ровно L от того, кто списывает. Таким образом, преподаватель хочет рассадить студентов так, чтобы между каждыми двумя студентами, которые могут списывать друг у друга, сидело бы ровно L - 1 других студентов. Помогите преподавателю найти такую рассадку. Примечание. Ясно, что в зависимости от того, с какого именно из двух студентов начинать считать, и в зависимости от того, в какую сторону считать, получится разное количество человек, сидящих между ними. Преподавателю требуется лишь, чтобы для каждой пары, начиная с хотя бы какого-нибудь из этих двух студентов, хотя бы в какую-нибудь сторону до другого насчитывался бы ровно L - 1 студент.

У нас есть две кучки камней, изначально в каждой по одному камню. За один ход можно добавлять один камень в одну из кучек, если в ней меньше N камней. Игра заканчивается, когда в обеих кучках будет N камней.

Не странно, что в нашей школе любят простые числа. Поэтому позиция в игре считается хорошей, если после приписывания к количеству камней в первой кучке количества камней во второй кучке получится простое число.

Например, если в первой кучке 12 камней, а во второй – 7, то позиция хорошая, т.к. число 127 простое.

Ваша задача найти такую последовательность ходов, при которой можно перейти из начальной позиции (1, 1) в конечную (N, N) через максимально возможное число хороших позиций. Например, для N = 4 одна из искомых последовательностей такова: 1; 1 -> 2; 1 -> 3; 1 -> 4; 1 -> 4; 2 -> 4; 3 -> 4; 4

Написать рекурсивную программу перевода целых чисел, не превосходящих 10⁹, из десятичной системы счисления в P-ичную (1  ≤  P  ≤  36)