--->
232 задач
<---
Источники
#868
Источники:
[
Командные олимпиады,
Московская командная олимпиада,
9-11 классы,
2008,
Лига Б,
Задача E
]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
Напишите программу, вычисляющую остаток от деления заданного «длинного» числа на заданную цифру.
Входные данные
В первой строке задана цифра K (1≤K≤9). Во второй строке задано натуральное число N, состоящее из не более чем 250 цифр.
Выходные данные
Выведите остаток от деления N на K.
Примеры
Входные данные | Выходные данные |
| 5 123456789 | 4 |
| 1 123 | 0 |
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
Пусть A — массив, состоящий изNэлементов A1,...,AN. Обозначим его максимальноеи минимальное значение как max(A) и min(A) соответственно. Вычислим сумму элементов S, S=A1+A2+…+AN. Заменим каждый элемент массива на разницу S и этого элемента: Ai:=S-Ai, 1iN. Такое преобразование массива A назовем операцией Confuse. Напишите программу, которая по массиву B, полученному в результате K–кратного применения операции Confuse к некоторому массиву A, вычислит разность max(A)-min(A).
Входные данные
Первая строка входного файла содержит целые числа N и K, где N — количество элементов массива B (2 N 10000), а K — количество применений операции Confuse к начальному массиву A, 1 K 100. Вторая строка файла содержит N элементов массива B. Элементы массива B — целые числа, принадлежащие диапазону от -2 000 000 000 до 2 000 000 000.
Выходные данные
Единственная строка выходного файла должна содержать целое число - разность max(A) и min(A).
Примеры
Входные данные
4 2 45 52 47 46
Выходные данные
7
#897
Темы:
[Двумерные массивы]
[Цикл for]
Даны две таблицы. В первой записана информация о школьниках (фамилия, имя и номер школы), а во второй – информация о результатах экзамена (фамилия, имя школьника и его оценка за экзамен). Требуется составить сводную таблицу, в которой будет указан номер школы и средняя оценка за экзамен всех учеников из этой школы (средняя оценка – это среднее арифметическое всех оценок, округленное до ближайшего сверху числа).
Входные данные
В первой строке вводится одно натуральное число N, не превосходящее 50 – количество школьников.
В следующих N строках вводится информация о школьниках в формате
Фамилия Имя Номер_Школы
Фамилия и имя не содержат пробелов, а номер школы – натуральное число, не превосходящее 2007.
В следующих N строках вводится информация об экзамене в формате
Фамилия Имя Оценка
Порядок учеников может быть иным, но имена и фамилии школьников такие же, как в предыдущем списке. Оценка – натуральное число от 2 до 5.
Гарантируется, что любые два школьника отличаются именем или фамилией.
Выходные данные
Вывести список, отсортированный по возрастанию номера школы, каждая строка которого имеет формат
Номер_Школы Средняя_Оценка
Примеры
Входные данные
4 Pete Ivanov 2 Vasya Petrov 2007 Nic Vasiliev 2 Ivan Nikolaev 2007 Ivan Nikolaev 5 Nic Vasiliev 4 Pete Ivanov 3 Vasya Petrov 5
Выходные данные
2 4 2007 5
Введем следующие операции надо прямоугольной таблицей символов. Пусть нам дана матрица \(А\), состоящая из \(m\) строк (первый индекс) и \(n\) столбцов (второй индекс). Определим результирующую матрицу \(В\) для каждой из операций следующим образом:
- Транспозиция относительно главной диагонали (код операции '1'): \(B_{j,i}=A_{i,j}\)
- Транспозиция относительно другой диагонали (код операции '2'): \(B_{n-j+1,m-i+1}=A_{i,j}\)
- Горизонтальное отражение (код операции 'H'): \(B_{m-i+1,j}=A_{i,j}\)
- Горизонтальное отражение (код операции 'V'): \(B_{i,n-j+1}=A_{i,j}\)
- Поворот на 90 ('A'), 180 ('B'), или 270 ('C') градусов по часовой стрелке: \(B_{j,m-i+1}=A_{i,j}\) (для \(90^{\circ}\))
- Поворот на 90 ('X'), 180 ('Y'), или 270 ('Z') градусов против часовой стрелки: \(B_{n-j+1,i}=A_{i,j}\) (для \(90^{\circ}\))
Входные данные
В первой строке входных данных находятся значения \(m\) и \(n\) (\(0 < m, n \leq 300\)). В каждой из следующих \(m\) строк находятся по \(n\) печатных символов (т.е. не используются символы с кодами от 33 до 126).
Последняя строка содержит описание операций, которые были выполнены над этой матрицей, путем записи без пробелов из кодов. Операции выполняются по порядку слева направо.
Выходные данные
Выведите сначала два целых числа \(-\) число строк и столбцов в результирующей матрице. Затем выведите саму матрицу в том же формате, что и во входных данных.
Примеры
Входные данные
3 4
{uf=
v-fn
("C%
1Выходные данные
4 3
{v(
u-"
ffC
=n%
#1010
Темы:
[Обход в ширину]
[Двумерные массивы]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
32 megabytes
Вы являетесь одним из разработчиков новой компьютерной игры. Игра происходит на прямоугольной доске, состоящей из W×H клеток. Каждая клетка может либо содержать, либо не содержать фишку (см. рисунок).
Важной частью игры является проверка того, соединены ли две фишки путем, удовлетворяющим следующим свойствам:
- Путь должен состоять из отрезков вертикальных и горизонтальных прямых.
- Путь не должен пересекать других фишек.
При этом часть пути может оказаться вне доски. Например:
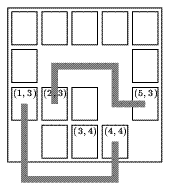
Фишки с координатами (1,3) и (4,4) могут быть соединены. Фишки с координатами (2,3) и (5,3) тоже могут быть соединены. А вот фишки с координатами (2,3) и (3,4) соединить нельзя – любой соединяющий их путь пересекает другие фишки.
Вам необходимо написать программу, проверяющую, можно ли соединить две фишки путем, обладающим вышеуказанными свойствами, и, в случае положительного ответа, определяющую минимальную длину такого пути (считается, что путь имеет изломы, начало и конец только в центрах клеток (или «мнимых клеток», расположенных вне доски), а отрезок, соединяющий центры двух соседних клеток, имеет длину 1).
Входные данные
Первая строка входного файла содержит два натуральных числа: W – ширина доски, H – высота доски (1≤W,H≤75). Следующие H строк содержат описание доски: каждая строка состоит ровно из W символов: символ «X» (заглавная английская буква «экс») обозначает фишку, символ «.» (точка) обозначает пустое место. Все остальные строки содержат описания запросов: каждый запрос состоит из четырёх натуральных чисел, разделённых пробелами – X1, Y1, X2, Y2, причём 1≤X1,X2≤W, 1≤Y1,Y2≤H. Здесь (X1, Y1) и (X2, Y2) – координаты фишек, которые требуется соединить (левая верхняя клетка имеет координаты (1,1)). Гарантируется, что эти координаты не будут совпадать (кроме последнего запроса; см. далее). Последняя строка содержит запрос, состоящий из четырёх чисел 0; этот запрос обрабатывать не надо. Количество запросов не превосходит 20.
Выходные данные
Для каждого запроса необходимо вывести одно целое число на отдельной строке – длину кратчайшего пути, или 0, если такого пути не существует.
Примеры
Входные данные
5 4 XXXXX X...X XXX.X .XXX. 2 3 5 3 1 3 4 4 2 3 3 4 0 0 0 0
Выходные данные
5 6 0
Входные данные
4 4 XXXX XXXX XXXX XXXX 1 1 2 1 2 2 3 2 1 1 3 1 3 4 4 3 2 1 2 4 1 1 2 2 0 0 0 0
Выходные данные
1 1 4 6 11 0
Выбрано
:
|