Разбиения числа \(n\) на слагаемые — это набор целых положительных чисел, сумма которых равна \(n\). При этом разбиения, отличающиеся лишь порядком слагаемых, считаются одинаковыми, поэтому можно считать, что слагаемые в разбиении упорядочены по неубыванию.
Например, существует 7 разбиений числа 5 на слагаемые:
|
5 = 1 + 1 + 1 + 1 + 1 5 = 1 + 1 + 1 + 2 5 = 1 + 1 + 3 5 = 1 + 2 + 2 5 = 1 + 4 5 = 2 + 3 5 = 5 |
В приведенном примере разбиения упорядочены лексикографически — сначала по первому слагаемому в разбиении, затем по второму, и так далее. В этой задаче вам потребуется по заданному разбиению на слагаемые найти следующее в лексикографическом порядке разбиение.
Входной файл содержит одну строку — разбиение числа \(n\) на слагаемые (\(1 \le n \le 100 000\)). Слагаемые в разбиении следуют в неубывающем порядке.
Выведите в выходной файл одну строку — разбиение числа \(n\) на слагаемые, следующее в лексикографическом порядке после приведенного во входном файле. Если во входном файле приведено последнее разбиение числа \(n\) на слагаемые, выведите «No solution».
5=1+1+3
5=1+2+2
5=5
No solution
Олег — известный поклонник соревнований по программированию. Он знает всех участников всех соревнований за последние десять лет и может про любого участника сказать, сколько задач решила команда с его участием на любом соревновании. И еще Олег очень любит теорию чисел.
В таблице результатов соревнования по программированию команды упорядочены по убыванию количества решенных задач. Олег называет таблицу результатов красивой, если для всех команд количество решенных ими задач равно нулю или является делителем количества задач на соревновании. Когда какая-нибудь команда сдает задачу, количество сданных задач у нее увеличивается на один. Никакая команда не может сдать две или более задач одновременно, также две команды не могут одновременно сдать задачу.
Глядя на красивую таблицу результатов, Олег заинтересовался: а сколько еще задач смогут суммарно сдать команды так, чтобы после каждой сданной задачи таблица результатов оставалась красивой? Помогите ему выяснить это.
Первая строка входного файла содержит два целых числа: \(n\) и \(m\) — количество команд и количество задач на соревновании, соответственно (\(1 \le n \le 100\), \(1 \le m \le 10^9\)). Вторая строка содержит n целых чисел, упорядоченных по невозрастанию: для каждой команды задано, сколько задач она решила. Гарантируется, что все отличные от нуля числа являются делителями числа \(m\).
Выведите в выходной файл одно число: максимальное количество задач, которое суммарно могут еще сдать команды так, чтобы после каждой сданной задачи таблица результатов оставалась красивой.
Комментарий к примеру тестов.
В приведенном примере команды на 4 и 5 месте могут сдать по одной задаче, команда на 6 месте три, а команда на 7 месте — 4. Суммарно таким образом команды смогут сдать 9 задач
7 12 12 6 4 3 3 1 0
9
На соревнованиях по прыжкам на лыжах с трамплина техника прыжка оценивается пятью судьями. Каждый судья ставит оценку от \(1\) до \(20\), после чего одна наименьшая и одна наибольшая оценки отбрасываются. Вам нужно написать программу, которая будет демонстрировать результаты прыжка для телетрансляции.
Она должна выводить пять оценок, которые поставили судьи, не меняя их порядка, а затем их сумму, и при этом брать в скобки те оценки, которые не учитываются при расчете суммы
На вход подается \(5\) натуральных чисел от \(1\) до \(20\), разделенных пробелом.
Выведите те же числа в том же порядке, взяв в скобки минимальное (а если их несколько – самое левое из них) и максимальное (а если их несколько – самое правое из них) число, а также сумму всех чисел, не взятых в скобки. Все числа (включая сумму) должны быть напечатаны в одной строке и разделены одним пробелом (внутри скобок пробелов быть не должно). Перед суммой должен стоять знак равенства, отделенный слева и справа одним пробелом. Порядок оценок должен быть такой же, как и во входных данных.
1 2 3 4 5
(1) 2 3 4 (5) = 9
10 11 10 11 10
(10) 11 10 (11) 10 = 31
Магическим квадратом называют таблицу, в которой записаны числа \(1, 2, 3, …\) по одному разу, так что сумма чисел в каждой строке и в каждом столбце равные. Мы расскажем вам об одном из методов построения магических квадратов (его называют сиамским). Он годится только для построения квадратов с нечетной стороной \((3\times 3, 5\times 5, …)\).
Поставим число \(1\) в верхнюю клетку центрального столбца. Далее будем двигаться по диагонали вправо-вверх, расставляя в клетки последовательно числа \(2, 3, 4, …\). Если мы вышли за пределы таблицы вверх, то нужно перейти к нижней клетке того же столбца и продолжить с нее. Если мы вышли за правую границу, нужно перейти к левой клетке той строки, куда мы должны были попасть. Если же мы одновременно вышли и вверх, и вправо, то нужно перейти в левую нижнюю клетку квадрата.
Если в следующей клетке на нашем пути уже стоит число, то вместо хода “вправо-вверх” нужно сделать ход “вниз” (опять же, если мы при этом выйдем за границы квадрата, нужно перейти к верхней клетке того же столбца). Примеры для квадратов \(3\times 3\) и \(5\times 5\) показаны на рисунках.
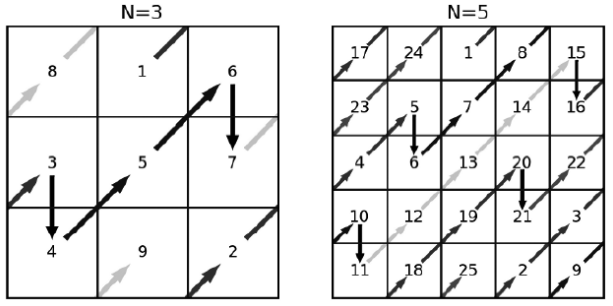
На вход подается одно натуральное нечетное число \(N\), не превосходящее \(30\) – размер квадрата.
Выведите числа, записанные в квадрате. Выравнивать числа по столбцам не обязательно. Обратите внимание: требуется вывести именно магический квадрат, полученный применением указанного метода.
3
8 1 6 3 5 7 4 9 2
5
17 24 1 8 15 23 5 7 14 16 4 6 13 20 22 10 12 19 21 3 11 18 25 2 9
Даны два массива чисел. Требуется вывести в выходной файл те элементы первого массива (в том порядке, в каком они идут в первом массиве), которых нет во втором массиве.
Во входном файле записано сначала число N - количество элементов в первом массиве, затем N чисел - элементы массива. Затем записано число M - количество элементов во втором массиве. Затем записаны элементы второго массива. Количество элементов каждого массива не превышает 100. Сами элементы - числа из диапазона Longint.
В выходной файл выведите те элементы первого массива, которых нет во втором в том порядке, в каком они идут в первом массиве.
7 3 1 3 4 2 4 12 6 4 15 43 1 15 1
3 3 2 12