Кроме Земли, пандорианцы уже много тысячелетий исследуют и другие планеты. Большой интерес для них в прошлом представляла планета Арракис. К сожалению, с началом исследований на Земле финансирование исследований на Арракисе было существенно урезано, и местным агентам-исследователям пришлось искать дополнительные источники дохода.
К счастью, пандорианцы очень хорошо разбираются в финансовых вопросах. Им не составило труда проанализировать политические, экономические и психологические тенденции, а также некоторые другие факторы, не имеющих названий на земных языках и на основе этих данных точно предсказать изменение стоимости воды на Арракисе на ближайший год. Как известно, вода на этой планете является главной ценностью после золота, на которое эту воду можно купить.
Изначально пандорианцы обладают запасом золота в 10 золотых слитков. Они решили в один из дней года купить на все это золото воды, а в какой-то последующий день продать всю купленную воду и получить прибыль за счет разницы стоимости. К примеру, если бы стоимость воды в день покупки составляла 1 литр за 4 золотых слитка, а стоимость воды в день продажи – 1 литр за 6 золотых слитков, то пандорианцы могли бы получить купить \(\frac{10}{4}=2.5\) литра воды, а продать они эту воду смогут за \(2.5 \times 6=15\) золотых слитков. Таким образом, прибыль пандорианцев составила бы \(15-10=5\) золотых слитков. Конечно же, пандорианцы хотят максимизировать свой доход в результате этих махинаций. Помогите им выбрать оптимальные дни для покупки и продажи воды!
В первой строке задано целое число 2 ≤ N ≤ 100 000 — количество дней в году на планете Арракис.
Во второй строке заданы N целых положительных чисел a i ( 1 ≤ i ≤ N , 1 ≤ a i ≤ 5000 ), задающих стоимость воды на Арракисе в день i .
Выведите два целых числа: первое число — номер дня, в который стоит купить воду, второе число — номер дня, в который следует воду продать. Дни нумеруются с единицы. Если оптимальных пар дней для покупки/продажи несколько, то выведите любую из них.
Выведите два нуля, если покупка и продажа воды по указанной схеме не принесет пандорианцам прибыли.
6 10 3 5 3 11 9
2 5
4 5 5 5 5
0 0
Компания RectanGas занимается добычей нефти уже с незапяматных времен и является бесспорным лидером в своей области. Маркетологи считают, что она стала такой успешной благодаря бессменному исполнительному директору. На нем стоит остановиться поподробнее.
Дело в том, что исполнительный директор совсем не изучал геометрию в школе и до сих пор считает, что кроме прямоугольников других геометрических фигур не существует. Более того, он никак не может поверить, что стороны прямоугольников могут быть не параллельными осям координат. Поэтому все нефтяные вышки строятся следующим образом: директор на карте отмечает четыре точки так, чтобы они образовывали прямоугольник со сторонами, параллельными осям координат карты, и приказывает строить нефтяные вышки на участках, соответствующим отмеченным точкам на карте. Эти нефтяные вышки за короткий промежуток времени добывают всю нефть, расположенную на соответствующем участке.
Компания RectanGas почти выполнила свой план по добыче нефти на май 2010 года. Для этого ей осталось добыть ровно S баррелей нефти. Заметим, что больше добывать нельзя, иначе компанию обвинят в монополии. Меньше добывать тоже нельзя, потому что исполнительный директор, будучи человеком пунктуальным, очень огорчится, что повлечет за собой увольнение сотрудников и всеобщую безработицу. Геологи, подробно изучив карту местности, определили количество залежей нефти на каждом участке и попросили Вас написать программу, определяющую координаты будущих нефтяных вышек с учетом всех требований.
Первая строка содержит три числа: размеры карты местности n и m и план по добыче нефти S ( 2 ≤ n , m ≤ 300 ; 0 ≤ S ≤ 10 7 ). Далее следуют n строк по m чисел a ij — количество залежей нефти на соответсвующем участке ( 0 ≤ a ij ≤ 10 6 )
В случае, если увольнения не миновать, выведите « - 1 » (без кавычек). В противном случае выведите четыре числа — координаты левой верхней и правой нижней вышек соответственно. Если вариантов ответа несколько, то выведите любой из них.
Обратите внимание, в этой задаче TL равен 500 мс.
Иллюстрация к первому примеру:
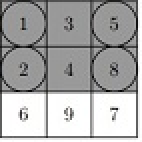
Сумма значений в угловых вышках равна 1 + 5 + 2 + 8 = 16
3 3 16 1 3 5 2 4 8 6 9 7
1 1 2 3
2 3 4 12 6 7 4 9 5
-1
На день рождения маленький Ипполит получил долгожданный подарок — набор дощечек с написанными на них буквами латинского алфавита. Теперь-то ему будет чем заняться долгими вечерами, тем более что мама обещала подарить ему в следующем году последовательность целых неотрицательных чисел, если он хорошо освоит этот набор. Ради такого богатства Ипполит готов на многое.
Прямо сейчас юный исследователь полностью поглощён изучением хорошести строк. Хорошестью строки называется количество позиций от 1 до L - 1 (где L — длина строки), таких, что следующая буква в строке является следующей по алфавиту. Например, хорошесть строки "abcdefghijklmnopqrstuvwxyz" равна 25, а строки "abdc" — только 1.
Ипполит размышляет над решением закономерно возникающей задачи: чему равна максимально возможная хорошесть строки, которую можно собрать, используя дощечки из данного набора? Вы-то и поможете ему с ней справиться.
Первая строка ввода содержит единственное целое число N — количество различных букв в наборе (1 ≤ N ≤ 26). Обратите внимание: в наборе всегда используются N первых букв латинского алфавита.
Следующие N строк содержат целые положительные числа ci — количество букв соответствующего типа (1 ≤ ci ≤ 109). Таким образом, первое число означает количество букв "a", второе число задаёт количество букв "b" и так далее.
Выведите единственное целое число — максимально возможную хорошесть строки, которую можно собрать из имеющихся дощечек.
3
1
1
1
2
2
3
4
3
В первом тесте имеется по одной дощечке с каждой из 3 различных букв. Ответ 2 достигается на строке "abc"
Каждый тест в данной задаче оценивается отдельно. Решение тестируется на основном наборе тестов только при прохождении всех тестов из условия. При этом тесты из условия не оцениваются.
Подзадача 1. Во всех тестах данной группы ci ≤ 100. Данная подзадача оценивается из 40 баллов.
Подзадача 2. Во всех тестах данной группы ci ≤ 1 000 000. Данная подзадача оценивается из 30 баллов.
Подзадача 3. Во всех тестах данной группы ci ≤ 109. Данная подзадача оценивается из 30 баллов.
Обычно в условии задач вам долго и нудно рассказывают, что нужно сделать. Но нам это показалось скучным. В этой задаче мы сделаем по-другому. Мы скажем вам, что не нужно делать:
Дана последовательность различных целых чисел. Переставьте её как вам угодно. Единственное требование: получившаяся последовательность не должна быть отсортирована — ни по возрастанию, ни по убыванию.
В первой строке содержится единственное число T (T ≤ 1 000) — количество тестов. Каждый тест состоит из двух строк:
В первой строке содержится единственное число N (3 ≤ N ≤ 1 000) — длина последовательности чисел.
В следующей строке содержатся N различных целых чисел — элементы последовательности. Гарантируется, что каждое число не меньше - 231 и не превосходит 231 - 1.
Для каждого теста в отдельной строке выведите новую последовательность.
2
5
1 2 3 4 5
8
3 1 4 47 5 9 2 6
5 1 4 3 2
3 1 4 47 5 9 2 6
Для моделирования различных объектов часто применяются так называемые клеточные поля. В простейшем случае – это прямоугольные таблицы, характеризующие некоторую область, а в каждой ячейке таблицы записывается какая-либо информация об исследуемом объекте. В биологии для моделирования распространения вирусов на плоской области в каждой ячейке помечается наличие вируса, а его распространение осуществляется в соседние ячейки по вертикали и горизонтали за одну единицу времени. Некоторые клетки обладают иммунитетом, заразить их невозможно и через них не распространяются вирусы.
Требуется написать программу, которая определяет минимально возможное число вирусов, с помощью которых можно заразить всю исследуемую прямоугольную область (за исключением защищённых клеток).
В приведённом примере таблица имеет размер \(4\times5\), в ней символом "I" помечены защищённые клетки. Видно, что двух вирусов достаточно для заражения всей области. Их можно поместить, например, в клетки, помеченные символом "V".

В первой входной строке записаны два натуральных числа \(M\) и \(N\) - размеры таблицы (количество строк и столбцов соответственно). Известно, что
\(1 \le M, N \le 100\). Во второй строке вначале записано одно число \(K\) - количество защищённых клеток, а далее записаны \(2K\) чисел – координаты этих клеток \(x_i\), \(y_i\) (\(0 \le k \le M \times N, 1 \le x_i \le M, 1 \le y_i \le N\)).
Программа должна вывести одно число – минимально возможное число вирусов.
4 5 3 1 3 2 1 2 2
2