В местном книжном магазине акция: "Возьми 3, заплати за 2 самых дорогих". То есть, каждый покупатель, который возьмет 3 книги, получит самую дешевую из них бесплатно. Разумеется, он может взять и больше книг, и, некоторым образом разделив их на группы по 3, получать самую дешевую в каждой группе бесплатно. Например, пусть цены книг, выбранных покупателем, будут следующие: 10 3 2 4 6 4 9. Он может разделить их на группы таким образом: (10, 3, 2), (4, 6, 4), (9). Тогда он получит книгу стоимостью 2 из первой группы и книгу стоимостью 4 из второй группы бесплатно. При этом из третьей группы он ничего не получит бесплатно, так как в ней всего 1 книга. Девушка, работающая в магазине, очень добрая и всегда хочет помочь покупателю заплатить как можно меньше денег за выбранные книги. Помогите ей для выбранных покупателем книг распределить их по группам так, чтобы сумма денег, в результате заплаченная покупателем, была минимальна.

Любимый всем кукольник Гепетто открыл новую пиццерию. Он хочет делать самую лучшую пиццу в городе, но не хочет иметь маленький ассортимент пицц.

Гепетто делает свои пиццы из N ингредиентов, пронумерованных от 1 до N . Всё было бы хорошо, но к сожалению он не может класть некоторые ингредиенты в одну пиццу.

Всего есть M пар ингредиентов, которые нельзя класть в одну пиццу. Помогите Гепетто узнать, сколько различных пицц он может cделать.

Марко обнаружил новую функцию на его телефоне - Т9. На его телефоне имеется стандартная клавиатура на 9 кнопок:

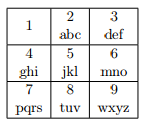
Для того чтобы вводить текст на этой клавиатуре необходимо несколько раз нажимать клавишу с соответствующей буквой. Точнее, если это первая буква на клавише, нужно нажать 1 раз, если вторая буква - 2 раза, и так далее. Например, если мы хотим ввести слово "giht", то необходимо нажать клавиши следующим образом: g-4 i-444 h-44 t-8. Новая возможность, которую открыл Марко, упрощает ввод текста, потому что больше не требуется нажимать по одной клавише несколько раз подряд - достаточно всего одного нажатия. Программа будет пытаться понять, какое слово из словаря вы пытаетесь ввести.

Марко довольно скептически относится к новым технологиями (как минимум к новым для него) и он боится, что ошибки будут довольно часто. Марко наизусть знает весь словарь мобильного телефона. Он состоит из N слов, состоящих из строчных латинских букв, длина каждого слова не превышает 1000000 символов. Марко даст массив нажатий на клавиши S длиной не более 1000, и хочет узнать как много слов из словаря он может получить при такой последовательности нажатий если используется функция Т9.

Дано 2 числа N и M , и их надо преобразовать следующим образом: выпишем их друг под другом (если числа имеют разную длину, дополним меньшее из них ведующими нулями) и будем сравнивать их отдельно в каждой цифре. Из того числа, где цифра меньше, эта цифра вычеркивается. Если цифры равны, то ничего не происходит. Если, в итоге, из числа вычеркнули все цифры, то вместо него надо вывести 'YODA' .

Найдите те числа, которые получатся в результате преобразования.

Юный Мирко - умный, но озорной мальчик, который часто бродит по паркам в поисках новых идей и друзей. В этот раз он встретился с пенсионерами, которые играли в карточную игру Белот. Они пригласили его помочь им подсчитать количество очков, выигранных в одной игре.

Каждая карта определяется мастью и символом. Набор из 4 карт называется рукой. В каждой игре одна из масть "бьет" все остальные и называется козырной. Количество очков в одной игре равно сумме победных очков всех карт из всех выигравших рук в игре. Мирко заметил, что пенсионерами было выиграно N рук, а козырная масть в игре была B .

Выигрышные очки карт (если масть козырная / если масть не козырная):

А : 11 / 11

K : 4 / 4

Q : 3 / 3

J : 20 / 2

T : 10 / 10

9 : 14 / 0

8 : 0 / 0

7 : 0 / 0

По данным выигравшим рукам и козырной масти определите количество очков, выигранных в этой игре.