Темы --> Информатика --> Алгоритмы --> Алгоритмы на графах --> Кратчайшие пути в графе --> Алгоритм Флойда
---> 20 задач <---
Источники
    Личные олимпиады(938 задач)
    Командные олимпиады(684 задач)
Страница: << 1 2 3 4 >> Отображать по:
#172
Флойд - 2
  
ограничение по времени на тест
5.0 second;
ограничение по памяти на тест
64 megabytes

Дан ориентированный взвешенный граф. Вам необходимо найти пару вершин, кратчайшее расстояние от одной из которых до другой максимально среди всех пар вершин.

Входные данные

В первой строке вводится единственное число N (1 <= N <= 100) – количество вершин графа. В следующих N строках по N чисел задается матрица смежности графа, где -1 означает отсутствие ребра между вершинами, а любое неотрицательное число – присутствие ребра данного веса. На главной диагонали матрицы – всегда нули.

Выходные данные

Выведите искомое максимальное кратчайшее расстояние.

Примеры
Входные данные
6
0 6 8 -1 -1 -1
5 0 5 -1 -1 -1
1 7 0 -1 -1 -1
-1 -1 -1 0 6 -1
-1 -1 -1 -1 0 3
-1 -1 -1 2 -1 0
Выходные данные
9
#173
Флойд - существование
  
ограничение по времени на тест
5.0 second;
ограничение по памяти на тест
64 megabytes

Дан ориентированный взвешенный граф. По его матрице смежности нужно для каждой пары вершин определить, существует ли кратчайший путь между ними или нет.

Комментарий: Кратчайший путь может не существовать по двум причинам:

  • Нет ни одного пути
  • Есть пути сколь угодно маленького веса

    • Входные данные

    В первой строке входного файла записано единственное число: \(N\) (\(1\leq N\leq 100\)) — количество вершин графа. В следующих \(N\) строках по \(N\) чисел — матрица смежности графа (\(j\)-е число в \(i\)-й строке соответствует весу ребра из вершины \(i\) в вершину \(j\)): число 0 обозначает отсутствие ребра, а любое другое число — наличие ребра соответствующего веса. Все числа по модулю не превышают 100.

    Выходные данные

    Выведите \(N\) строк по \(N\) чисел. \(j\)-е число в \(i\)-й строке должно соответствовать кратчайшему пути из вершины \(i\) в вершину \(j\). Число должно быть равно 0, если пути не существует, 1, если существует кратчайший путь, и 2, если пути существуют, но бывают пути сколь угодно маленького веса.

    Примеры
    Входные данные
    5
0 1 2 0 0
1 0 3 0 0
2 3 0 0 0
0 0 0 0 -1
0 0 0 -1 0
    Выходные данные
    1 1 1 0 0 
1 1 1 0 0 
1 1 1 0 0 
0 0 0 2 2 
0 0 0 2 2
    #999
    Юный поджигатель
      
    ограничение по времени на тест
    1.0 second;
    ограничение по памяти на тест
    64 megabytes
    Дан граф на клетчатом поле, вершины которого могут находится в целых клетках и соединяться по линиям сетки или по диагонали клеток (в случае пересечения двух клеток там также создается вершина). Необходимо найти вершину, расстояние от которой до самой дальней минимально.

    На клеточном поле введена система координат так, что центр координат находится в точке пересечения линий сетки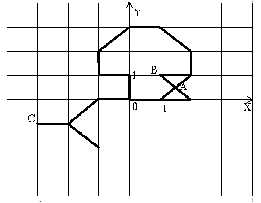 и оси направлены вдоль линий сетки.

    На этом поле выложили связную фигуру, состоящую из спичек. Использовались спички двух типов:

    • Спички длины 1 выкладывались по сторонам клеток.
    • Спички длины выкладывались по диагоналям клеток.

    Ребенок хочет сжечь фигуру. При этом он может поджечь ее в одной точке, имеющей целочисленные координаты (например, в точке A на рисунке поджигать фигуру нельзя, а в точках B и C — можно).

    Известно, что огонь распространяется вдоль спички равномерно (но по каждой спичке — со своей скоростью). Спичка может гореть в нескольких местах (например, когда она загорается с двух концов; или когда в середине диагональной спички огонь перекидывается с одной спички на другую — огонь расползается по вновь подожженной спичке в обе стороны).

    Напишите программу, которая определит, в какой точке нужно поджечь фигуру, чтобы она сгорела за минимальное время.

    Входные данные

    Во входном файле записано сначала число N — количество спичек (1N40). Затем идет N пятерок чисел вида X1, Y1, X2, Y2, T, задающих координаты концов спички и время ее сгорания при условии, что она будет подожжена с одного конца (гарантируется, что каждая спичка имеет длину 1 или , все спички образуют связную фигуру, и положение никаких двух спичек не совпадает). Все координаты — целые числа, по модулю не превышающие 200, время сгорания — натуральное число, не превышающее 107.

    Выходные данные

    Выведите координаты целочисленной точки, в которой нужно поджечь фигуру, чтобы она сгорела за наименьшее время, а затем время, за которое в этом случае фигура сгорит. Время должно быть выведено с точностью не менее 2-х знаков после десятичной точки. Если решений несколько, выведите любое из них.

    Примеры
    Входные данные
    1
0 0 1 1 1
    Выходные данные
    0 0
1.00
    Входные данные
    5
0 0 0 1 1
1 0 0 1 10
0 0 1 0 1
0 0 1 1 1
2 2 1 1 1
    Выходные данные
    0 0
3.25
    Входные данные
    3
1 1 1 2 10
1 2 2 2 10
1 1 2 2 50
    Выходные данные
    2 2
35.00
    #1329
    Кладоискатель
      
    ограничение по времени на тест
    1.0 second;
    ограничение по памяти на тест
    64 megabytes

    Кладоискателю Васе попалась карта древнего подземелья. Подземелье представляет собой лабиринт размера \(N \times M\) (\(1 \le N, M \le 100\), \(N \times M \le 100\)). Каждая клетка лабиринта либо пуста и по ней можно пройти, либо содержит стену. Из клетки можно переходить только в смежную по стене клетку (так, у каждой клетки может быть не более 4 смежных).

    В одной из клеток находится клад, который и хочет достать Вася. В лабиринте есть \(K\) входов, из которых Вася может начать свой путь.

    Требуется определить, с какого входа Васе нужно начать свой путь, чтобы пройденное расстояние до клада было наименьшим. Если таких входов несколько, нужно вывести вход с наименьшим номером.

    Входные данные

    Первая строка содержит 2 числа \(N\) и \(M\), задающие размеры лабиринта. Далее следует описание лабиринта: \(N\) строк по \(M\) символов в каждой. 0 означает, что клетка свободна; 1, что в клетке находится стена. Символ * обозначает клетку с сокровищем (такая клетка в лабиринте ровно одна).

    В \((N+2)\)-й строке находится число \(K\) (\(1 \le K \le N \times M\)) -- количество входов в лабиринт. Далее в \(K\) строках содержатся координаты входов. Так, в \(i\)-й строке содержатся числа \(x_i\) и \(y_i\), означающие,что \(i\)-й вход расположен в \(x_i\)-й строке и в \(y_i\)-м столбце (\(1 \le x_i \le N, 1 \le y_i \le M\)). Гарантируется, что координаты входов попарно различны, и то, что все входы расположены в пустых клетках. Ни один из входов не находится в клетке с сокровищем.

    Выходные данные

    Необходимо вывести одно число - искомый номер входа (нумерация начинается с 1). Если до сокровища невозможно добраться, выведите -1.

    Примеры
    Входные данные
    5 5
00000
00000
10*00
01111
00000
4
1 1
1 5
4 1
5 5
    Выходные данные
    1
    Входные данные
    3 3
010
1*1
010
4
1 1
1 3
3 1
3 3
    Выходные данные
    -1
    #1330
    Маршрут кладоискателя
      

    Вася из задачи A по-прежнему занят поиском кладов. Более того, у него появились последователи. Один из таких последователей попросил Васю помочь в своих поисках. Так, по карте сокровищ Васю просят восстановить кратчайший путь до клада. Конфигурация лабиринта совпадает с конфигурацией, описанной в задаче A (поле \(N \times M\) (\(1 \le N, M \le 100\), \(N \times M \le 100\))), в одной клетке которого находится клад, в \(K\) клетках находятся входы в лабиринт).

    Требуется вывести искомый путь.

    Входные данные

    Первая строка содержит 2 числа \(N <= 100\) и \(M <= 100\), задающие размеры лабиринта. Далее следует описание лабиринта: \(N\) строк по \(M\) символов в каждой. 0 означает, что клетка свободна; 1, что в клетке находится стена. Символ * обозначает клетку с сокровищем (такая клетка в лабиринте ровно одна).

    В \((N+2)\)-й строке находится число \(K\) (\(1 \le K \le N \times M\)) -- количество входов в лабиринт. Далее в \(K\) строках содержатся координаты входов. Так, в \(i\)-й строке содержатся числа \(x_i\) и \(y_i\), означающие,что \(i\)-й вход расположен в \(x_i\)-й строке и в \(y_i\)-м столбце (\(1 \le x_i \le N, 1 \le y_i \le M\)). Гарантируется, что координаты входов попарно различны, и то, что все входы расположены в пустых клетках. Ни один из входов не находится в клетке с сокровищем.

    Выходные данные

    В первой строке вывести одно число - длину кратчайшего маршрута. В следующих строках необходимо вывести кратчайший маршрут. Каждую клетку маршрута (включая начальную и конечную) вывести на отдельной строке в формате \(x_i\) \(y_i\), где \(x_i\) - строка клетки, а \(y_i\) - столбец клетки.

    Если существует несколько путей минимальной длины, выведите любой. Если до сокровища невозможно добраться, в единственной строке выведите -1.

    Примеры
    Входные данные
    5 5
00000
00000
10*00
01111
00000
4
1 1
1 5
4 1
5 5
    Выходные данные
    4
    Входные данные
    3 3
010
1*1
010
4
1 1
1 3
3 1
3 3
    Выходные данные
    -1
    Страница: << 1 2 3 4 >> Отображать по:
    Выбрано
    :
    Отменить
    |
    Добавить в контест