--->
121 задач
<---
Источники
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
256 megabytes
На кольце нанесена надпись, состоящая из заглавных английских букв и пробелов. Суммарное количество символов в надписи не превышает 180.
Надпись нанесена таким образом, что:
1. все буквы (даже пробелы) имеют одинаковую ширину (то есть дуги, соответствующие каждому символу одинаковы);
2. надпись охватывает все кольцо, между последним и первым символом нет пробела.
Юля смотрит на кольцо со стороны \(k\)-го символа от начала надписи (символы нумеруются с 1, слева направо).
Определите, какую часть надписи видит Юля.
Вывести следует только символы, видимые целиком.
Символ считается видимым, если угол между его дальней границей и линией взгляда составляет не более 60 градусов.
Входные данные
На первой строке вводится число \(k\) (натуральное, не превышает длины надписи). На второй строке - текст надписи (строка, не короче 3 и не длиннее 180 символов, состоящая из заглавных английских букв и пробелов.
Выходные данные
Требуется вывести строку - часть надписи, которая будет видимой при данном положении кольца.
Примеры
Входные данные
2 ABCD
Выходные данные
B
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
256 megabytes
Некоторый алгоритм шифрования устроен следующим образом.
Исходная строка разбивается на блоки по 36 символов. Если в конце остается часть, которой недостаточно для полного блока, то она не шифруется.
Шифрование происходит с помощью квадратного трафарета, в котором имеется 9 прорезей для записи символов.
Пример трафарета показан на рисунке.
Например, если в начале блока шло слово «Криптография», то его символы будут расположены вот так:
Символы из таблицы выписываются в порядке слева направо и сверху вниз - таким образом получается зашифрованный блок.
Затем трафарет возвращается в исходное положение и операция повторяется для остальных блоков.
Гарантируется, что трафарет корректен (то есть в процессе шифрования одного блока над каждой клеткой таблицы прорезь появляется ровно один раз).
Дана строка, состоящая из английских букв (заглавных и строчных) и пробелов. Также дан трафарет. Напишите программу шифрования данной строки по трафарету.
Входные данные
В первой строке находится исходный текст (одна непустая строка длинной не более 200 символов).
В следующих 6 строках описан трафарет в следующем формате: закрытая клетка обозначается символом ‘#’ (решетка), прорезь обозначается символом ‘.’ (точка).
Например, трафарет из условия задачи будет вводиться так:
.##### #..### ###.## .###.# ###### #..#.#
Выходные данные
Выведите строку, полученную в результате шифрования исходного текста.
Примеры
Входные данные
ABCDE .##### #..### ###.## .###.# ##### #..#.#
Выходные данные
ABCDE
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes
Вася не только играет в компьютерные и настольные игры, но и решает олимпиадные задачи по программированию. Три года назад он зарегистрировался на одном очень популярном сайте—KodeForces (KF) и с тех пор уже сдал целых 11 задач из архива! Вася не намерен останавливаться на достигнутом и планирует решить еще 1-2 задачи в ближайший месяц - полтора.
Однако сейчас его мозг занят совсем другой проблемой. Раз в год на KF случается чудо — любой пользователь сайта может изменить свой логин (имя пользователя). «Такую возможность упускать нельзя!», — подумал Вася и решил сделать свой логин лаконичным , т.е. состоящим из одинаковых букв.
Однако в этом году все не так то просто... Изменять логин можно только согласно следующему правилу: можно выбрать все одинаковые буквы имени и заменить их все на предыдущую или последующую букву в алфавитном порядке. Например, можно заменить все e на d или f . При этом, z можно заменить на a или y , а a на z или b .
Вася несколько ленив, поэтому, прежде чем начать изменение имени, он хочет посчитать минимальное количество применений описанного выше правила, позволяющее сделать логин лаконичным. Что если это число окажется слишком большим, и он потратит слишком много времени и пропустит очередной рейд в WoW-ке?
Входные данные
В первой и единственной строке находится исходный логин Васи—строка из маленьких латинских букв длиной не более 1000 символов.
Выходные данные
Выведите единственное число—минимальное количество действий, за которое можно сделать логин Васи лаконичным.
Примечание
В первом примере Вася может сначала заменить все буквы a на b , а затем буквы b на c . Т.е.aaac => bbbc => cccc.
Во втором примере Васе необходимо заменить все a на b , а затем изменить букву c на b . Т.е. bbaaaac => bbbbbbc => bbbbbbb.
Примеры
Входные данные
aaac
Выходные данные
2
Входные данные
bbaaaac
Выходные данные
2
#113558
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
Марко обнаружил новую функцию на его телефоне - Т9. На его телефоне имеется стандартная клавиатура на 9 кнопок:
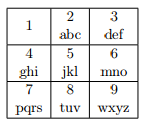
Для того чтобы вводить текст на этой клавиатуре необходимо несколько раз нажимать клавишу с соответствующей буквой. Точнее, если это первая буква на клавише, нужно нажать 1 раз, если вторая буква - 2 раза, и так далее. Например, если мы хотим ввести слово "giht", то необходимо нажать клавиши следующим образом: g-4 i-444 h-44 t-8. Новая возможность, которую открыл Марко, упрощает ввод текста, потому что больше не требуется нажимать по одной клавише несколько раз подряд - достаточно всего одного нажатия. Программа будет пытаться понять, какое слово из словаря вы пытаетесь ввести.
Марко довольно скептически относится к новым технологиями (как минимум к новым для него) и он боится, что ошибки будут довольно часто. Марко наизусть знает весь словарь мобильного телефона. Он состоит из N слов, состоящих из строчных латинских букв, длина каждого слова не превышает 1000000 символов. Марко даст массив нажатий на клавиши S длиной не более 1000, и хочет узнать как много слов из словаря он может получить при такой последовательности нажатий если используется функция Т9.
Входные данные
Первая строка содержит единственное целое число N ( 1 ≤ N ≤ 1000 ) - количество слов в словаре. Каждая из следующих N строк содержит одно слово из словаря S i ( 1 ≤ | S i | ≤ 1000000 ). Последняя строка содержит строку S ( 1 ≤ | S | ≤ 1000 ), состоящую из цифр от 2 до 9.
Выходные данные
Выведите единственное целое число - количество слов из словаря, которые можно получить при данной последовательности нажатий.
Примеры
Входные данные
3 tomo mono dak 6666
Выходные данные
1
Входные данные
2 ja la 52
Выходные данные
2
Входные данные
3 dom fon tom 366
Выходные данные
2
#113572
Темы:
[Строки]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
Хан не хотел учиться один, поэтому он пригласил своего друга Доминика позаниматься вместе с ним. После того, как они решили рекордное количество задач за вечер, Доминик поехал домой. Внезапно его остановила полиция, подозревая, что он водил в пьяном виде. Чтобы проверить Доминика, полицейские начали задавать ему вопросы.
Полицейский: Давайте начнём с чего-то простого. Какова асимптотика сортировки пузырьком?
Доминик: О, это просто. O ( n 2 ) .
Полицейский: Скажите английский алфавит наоборот.
Доминик: Легко, zyxwvutsrqponmlkjihgfedcba.
Полицейский: Вы просто запомнили это. Представьте, что строчные буквы латинского алфавита записаны по кругу по часовой стрелке. Начинайте с буквы 'a' и называйте все буквы подряд. После каждой сказанной буквы я могу приказать теперь называть в обратном порядке, спросить сколько раз была названа какая-то буква или ничего не делать. Приступайте.
Доминик: Хм... a, b, c...
Возможно, Доминик не настолько трезв, чтобы решить эту задачу. Помогите ему.
Входные данные
Первая строка содержит одно целое число Q ( 1 ≤ Q ≤ 10 5 ) – количество приказов полицейского. Каждая из последующих Q строк содержит один из приказов в формате "SMJER n" или "UPIT n x". Приказ первого типа обозначает, что после n -й сказанной буквы требуется поменять направление. Приказ второго типа обозначает, что Доминик должен сказать, сколько раз он произнес букву x после n сказанных букв.
Во всех запросах 1 ≤ n ≤ 10 9 , а x – строчные латинские буквы. В запросах n идут в строго возрастающем порядке.
Выходные данные
Для каждого запроса вида "UPIT n x", выведите ответ на этот запрос, каждый в отдельной строке, в том же порядке, что и в вводе.
Система оценки
40 баллов: n ≤ 1000
60 баллов: n ≤ 10 5
100 баллов: n ≤ 10 9
Примечание
В первом примере Доминик говорит a, b, c, d, c, b, a, z, y, x.
Во втором примере Доминик говорит a, z, a, z, y, x, w.
Примеры
Входные данные
5 UPIT 1 b UPIT 3 b SMJER 4 UPIT 7 a UPIT 10 z
Выходные данные
0 1 2 1
Входные данные
5 SMJER 1 SMJER 2 SMJER 3 UPIT 5 a UPIT 7 w
Выходные данные
2 1
Входные данные
4 UPIT 100 a UPIT 200 c UPIT 300 a UPIT 400 b
Выходные данные
4 8 12 16
Выбрано
:
|